Uploaded byLiveOnlineClassesInd
PPTX, PDF199 views

Pythagoras Theorem Graphs

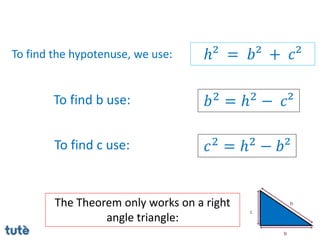
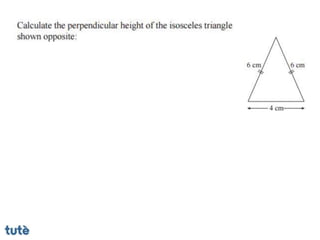
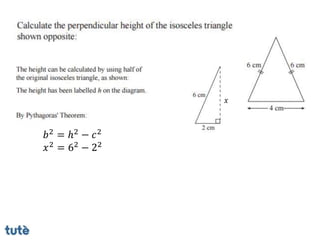
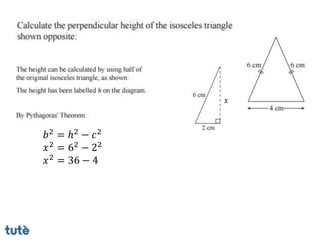
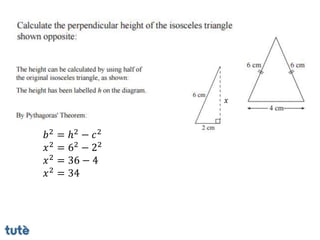
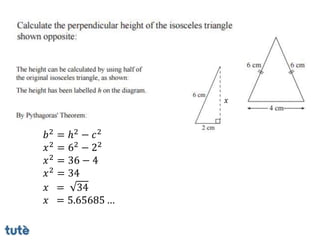
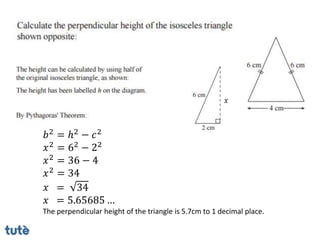
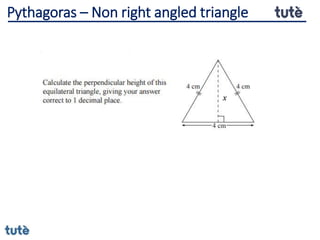
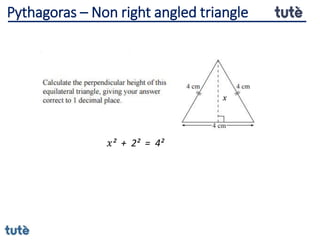
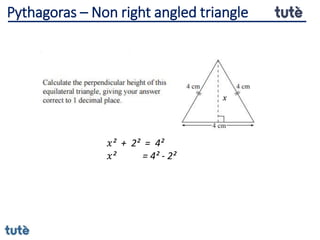
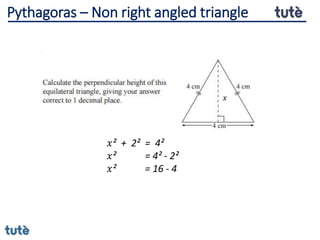
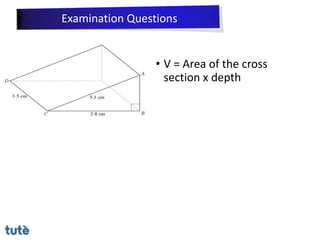
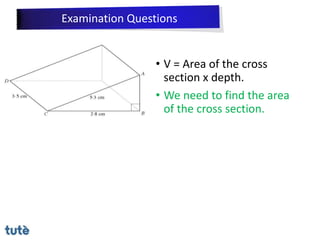
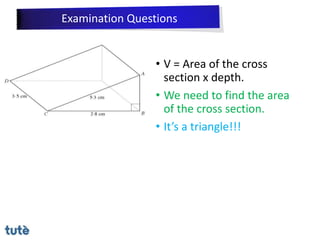
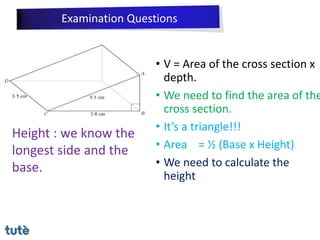
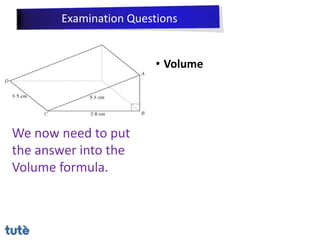
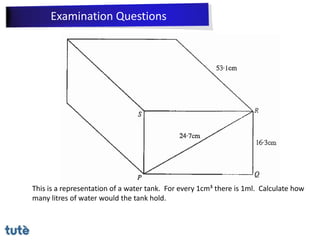
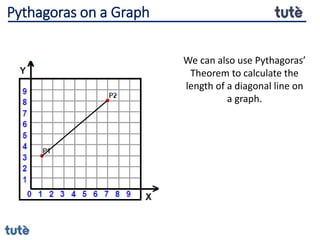
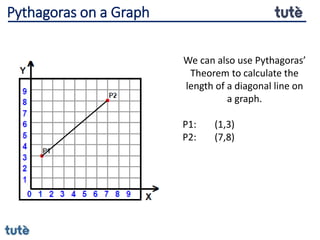
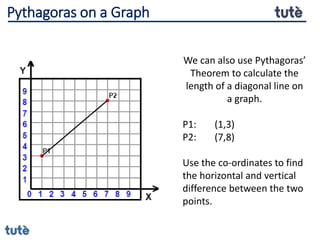
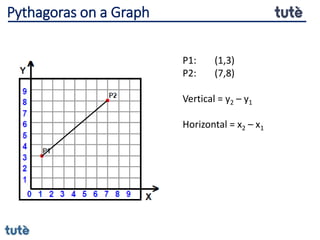
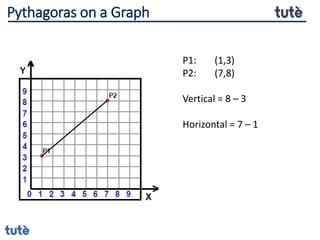
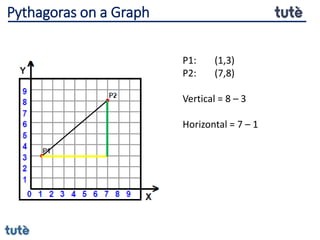
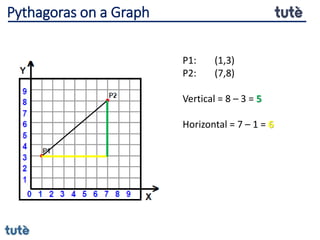
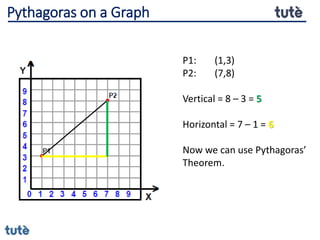
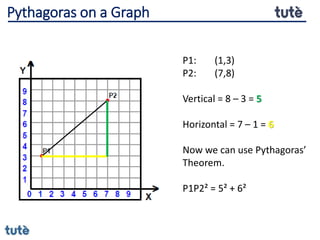
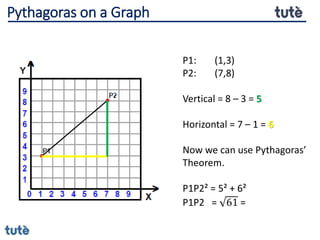
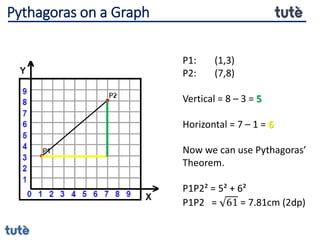
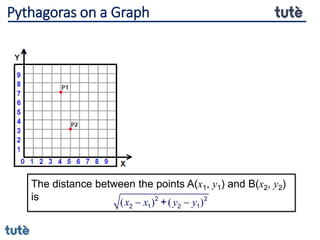
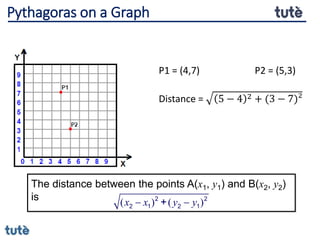
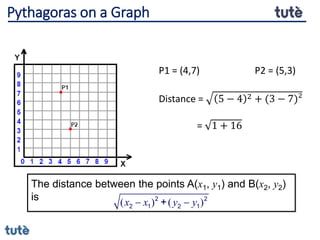
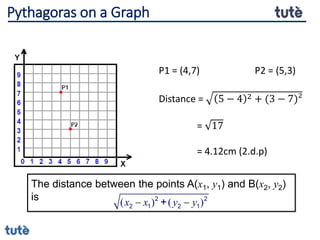
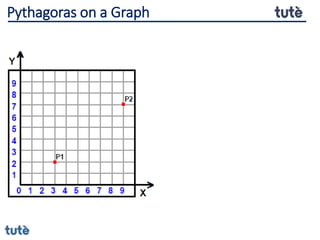
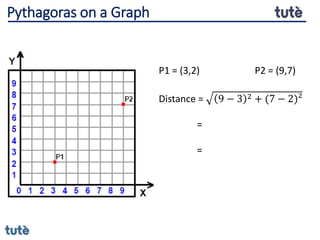
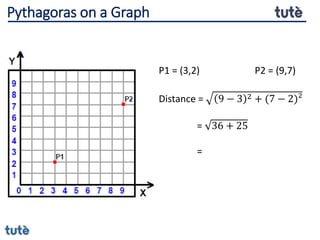
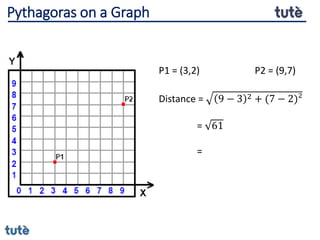
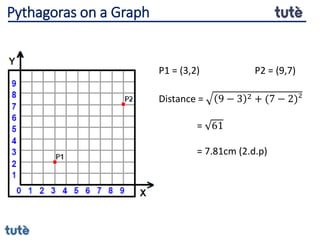
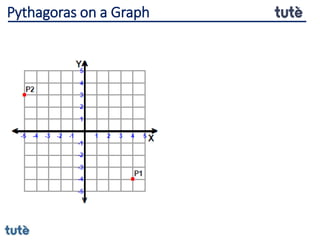
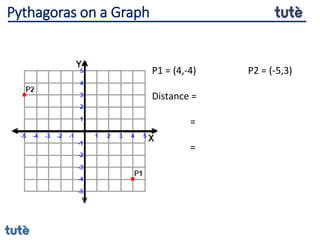
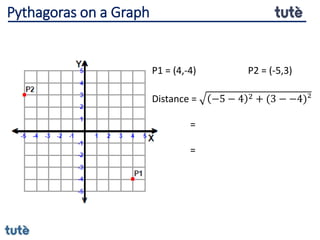
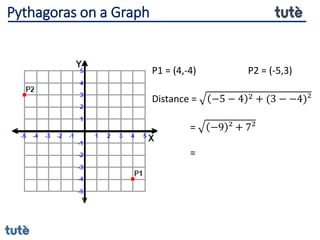
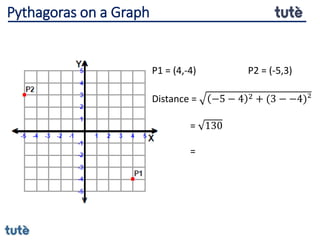
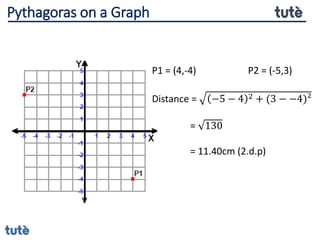
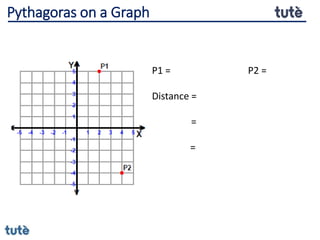
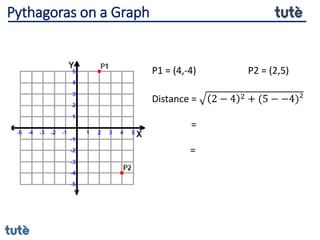
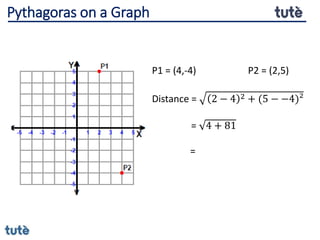
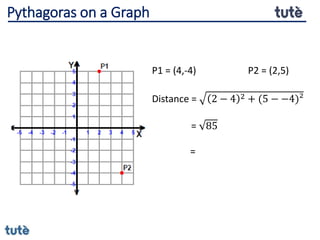
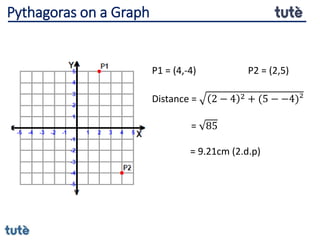
This document discusses how to apply Pythagoras' theorem to calculate distances and lengths in triangles, both right-angled and non-right angled. It provides examples of using the theorem to solve examination questions involving finding lengths, areas, perimeters, volumes, and calculating how much water a tank can hold.

Embed presentation

Download to read offline
How can we apply Pythagoras’ Theorem in graphs and other triangles? Learning Objective
• To revise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes Learning Outcomes
To find c use: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a _________________:
To find c use: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a _________________:
To find c use: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a _________________:
To find c use: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a _________________:
To find c use: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a right angle triangle:
Learning Outcomes • To revise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
Learning Outcomes • To revise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
Edexel Pythagoras Question
Edexel Pythagoras Question We use Pythagoras’ Theorem to calculate the distance between Norwich and York.
Edexel Pythagoras Question We use Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 =?2 +?2
Edexel Pythagoras Question We use Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 =?2 +?2 b c
Edexel Pythagoras Question We use Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 b c
Edexel Pythagoras Question We use Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 ℎ2 = 1682 + 1572 b c
Edexel Pythagoras Question We use Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 ℎ2 = 1682 + 1572 ℎ2 = 52873 b c
Edexel Pythagoras Question We use Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 ℎ2 = 1682 + 1572 ℎ2 = 52873 ℎ = 52873 b c
Edexel Pythagoras Question We use Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 ℎ2 = 1682 + 1572 ℎ2 = 52873 ℎ = 52873 ℎ = 229.94𝑘𝑚 (𝑡. 2. 𝑑. 𝑝) b c
𝑏2 = ℎ2 − 𝑐2 𝑥
𝑏2 = ℎ2 − 𝑐2 𝑥2 = 62 − 22 𝑥
𝑏2 = ℎ2 − 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥
𝑏2 = ℎ2 − 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥2 = 34 𝑥
𝑏2 = ℎ2 − 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥2 = 34 𝑥 = 34 𝑥
𝑏2 = ℎ2 − 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥2 = 34 𝑥 = 34 𝑥 = 5.65685 … 𝑥
𝑏2 = ℎ2 − 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥2 = 34 𝑥 = 34 𝑥 = 5.65685 … The perpendicular height of the triangle is 5.7cm to 1 decimal place. 𝑥
Pythagoras – Non right angled triangle 𝑥
𝑥² + 2² = 4² Pythagoras – Non right angled triangle 𝑥
𝑥² + 2² = 4² 𝑥² = 4² - 2² Pythagoras – Non right angled triangle 𝑥
𝑥² + 2² = 4² 𝑥² = 4² - 2² 𝑥² = 16 - 4 Pythagoras – Non right angled triangle 𝑥
𝑥² + 2² = 4² 𝑥² = 4² - 2² 𝑥² = 16 – 4 𝑥 = 12 Pythagoras – Non right angled triangle 𝑥
𝑥² + 2² = 4² 𝑥² = 4² - 2² 𝑥² = 16 – 4 𝑥 = 12 𝑥 = 3.5cm (1.d.p) Pythagoras – Non right angled triangle 𝑥
a) Calculate the length of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. Examination Questions
a) Calculate the length of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 Examination Questions
a) Calculate the length of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = √52 = 7.211102551 Examination Questions
a) Calculate the length of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm Examination Questions
a) Calculate the length of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm b) Area = ½ x 4 x 6 Examination Questions
a) Calculate the length of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm b) Area = ½ x 4 x 6 = 12 cm² Examination Questions
a) Calculate the length of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm b) Area = ½ x 4 x 6 = 12 cm² c) P = 4 + 6 + 7.211102551 Examination Questions
a) Calculate the length of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm b) Area = ½ x 4 x 6 = 12 cm² c) P = 4 + 6 + 7.211102551 = 17.2 cm Examination Questions
Examination Questions
• V = Area of the cross section x depth Examination Questions
• V = Area of the cross section x depth. • We need to find the area of the cross section. Examination Questions
• V = Area of the cross section x depth. • We need to find the area of the cross section. • It’s a triangle!!! Examination Questions
• V = Area of the cross section x depth. • We need to find the area of the cross section. • It’s a triangle!!! • Area = ½ (Base x Height) • We need to calculate the height Examination Questions
• V = Area of the cross section x depth. • We need to find the area of the cross section. • It’s a triangle!!! • Area = ½ (Base x Height) • We need to calculate the height Height : we know the longest side and the base. Examination Questions
• Pythagoras • a² = b² + c² • 5.3² = 2.8²+c² • c² = 5.3²-2.8² • = 20.25 • c = 20.25 • = 4.5 Height : we know the longest side and the base. Examination Questions
• Volume We now need to put the answer into the Volume formula. Examination Questions
• Volume • V = ½(4.5x2.8) x 3.5 We now need to put the answer in to the Volume formula. Examination Questions
• Volume • V = ½(4.5x2.8) x 3.5 • = ½(12.6) x 3.5 • = 6.3 x 3.5 • = 22.05cm³ We now need to put the answer in to the Volume formula. Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! Examination Questions
First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. Examination Questions
First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 = 16064.2cm³ Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 = 16064.2cm³ Not there yet! Now we calculate the litres 1cm³ = 1ml, 1000 ml = 1L Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 = 16064.2cm³ Not there yet! Now we calculate the litres 1cm³ = 1ml, 1000 ml = 1L Hence: 16064.2 ÷ 1000 = Examination Questions
This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 = 16064.2cm³ Not there yet! Now we calculate the litres 1cm³ = 1ml, 1000 ml = 1L Hence: 16064.2 ÷ 1000 = 16.06L (2dp) Examination Questions
Learning Outcomes • To revise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
Learning Outcomes • To revise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
We can also use Pythagoras’ Theorem to calculate the length of a diagonal line on a graph. Pythagoras on a Graph
We can also use Pythagoras’ Theorem to calculate the length of a diagonal line on a graph. P1: (1,3) P2: (7,8) Pythagoras on a Graph
We can also use Pythagoras’ Theorem to calculate the length of a diagonal line on a graph. P1: (1,3) P2: (7,8) Use the co-ordinates to find the horizontal and vertical difference between the two points. Pythagoras on a Graph
P1: (1,3) P2: (7,8) Vertical = y2 – y1 Horizontal = x2 – x1 Pythagoras on a Graph
P1: (1,3) P2: (7,8) Vertical = 8 – 3 Horizontal = 7 – 1 Pythagoras on a Graph
P1: (1,3) P2: (7,8) Vertical = 8 – 3 Horizontal = 7 – 1 Pythagoras on a Graph
P1: (1,3) P2: (7,8) Vertical = 8 – 3 = 5 Horizontal = 7 – 1 = 6 Pythagoras on a Graph
P1: (1,3) P2: (7,8) Vertical = 8 – 3 = 5 Horizontal = 7 – 1 = 6 Now we can use Pythagoras’ Theorem. Pythagoras on a Graph
P1: (1,3) P2: (7,8) Vertical = 8 – 3 = 5 Horizontal = 7 – 1 = 6 Now we can use Pythagoras’ Theorem. P1P2² = 5² + 6² Pythagoras on a Graph
P1: (1,3) P2: (7,8) Vertical = 8 – 3 = 5 Horizontal = 7 – 1 = 6 Now we can use Pythagoras’ Theorem. P1P2² = 5² + 6² P1P2 = 61 = Pythagoras on a Graph
P1: (1,3) P2: (7,8) Vertical = 8 – 3 = 5 Horizontal = 7 – 1 = 6 Now we can use Pythagoras’ Theorem. P1P2² = 5² + 6² P1P2 = 61 = 7.81cm (2dp) Pythagoras on a Graph
The distance between the points A(x1, y1) and B(x2, y2) is ( ) ( ) x x y y   2 2 2 1 2 1 + Pythagoras on a Graph
The distance between the points A(x1, y1) and B(x2, y2) is ( ) ( ) x x y y   2 2 2 1 2 1 + P1 = (4,7) P2 = (5,3) Distance = 5 − 4 2 + (3 − 7)² Pythagoras on a Graph
The distance between the points A(x1, y1) and B(x2, y2) is ( ) ( ) x x y y   2 2 2 1 2 1 + P1 = (4,7) P2 = (5,3) Distance = 5 − 4 2 + (3 − 7)² = 1 + 16 Pythagoras on a Graph
The distance between the points A(x1, y1) and B(x2, y2) is ( ) ( ) x x y y   2 2 2 1 2 1 + P1 = (4,7) P2 = (5,3) Distance = 5 − 4 2 + (3 − 7)² = 17 = 4.12cm (2.d.p) Pythagoras on a Graph
Pythagoras on a Graph
P1 = (3,2) P2 = (9,7) Distance = 9 − 3 2 + (7 − 2)² = = Pythagoras on a Graph
P1 = (3,2) P2 = (9,7) Distance = 9 − 3 2 + (7 − 2)² = 36 + 25 = Pythagoras on a Graph
P1 = (3,2) P2 = (9,7) Distance = 9 − 3 2 + (7 − 2)² = 61 = Pythagoras on a Graph
P1 = (3,2) P2 = (9,7) Distance = 9 − 3 2 + (7 − 2)² = 61 = 7.81cm (2.d.p) Pythagoras on a Graph
Pythagoras on a Graph
P1 = (4,-4) P2 = (-5,3) Distance = = = Pythagoras on a Graph
P1 = (4,-4) P2 = (-5,3) Distance = −5 − 4 2 + (3 − −4)² = = Pythagoras on a Graph
P1 = (4,-4) P2 = (-5,3) Distance = −5 − 4 2 + (3 − −4)² = −9 ² + 7² = Pythagoras on a Graph
P1 = (4,-4) P2 = (-5,3) Distance = −5 − 4 2 + (3 − −4)² = 130 = Pythagoras on a Graph
P1 = (4,-4) P2 = (-5,3) Distance = −5 − 4 2 + (3 − −4)² = 130 = 11.40cm (2.d.p) Pythagoras on a Graph
P1 = P2 = Distance = = = Pythagoras on a Graph
P1 = (4,-4) P2 = (2,5) Distance = 2 − 4 2 + (5 − −4)² = = Pythagoras on a Graph
P1 = (4,-4) P2 = (2,5) Distance = 2 − 4 2 + (5 − −4)² = 4 + 81 = Pythagoras on a Graph
P1 = (4,-4) P2 = (2,5) Distance = 2 − 4 2 + (5 − −4)² = 85 = Pythagoras on a Graph
Pythagoras on a Graph P1 = (4,-4) P2 = (2,5) Distance = 2 − 4 2 + (5 − −4)² = 85 = 9.21cm (2.d.p)
Learning Outcomes • To revise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
Learning Outcomes • To revise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes

More Related Content

PDF
Geometry Section 1-2
byJimbo Lamb
 
PDF
Geometry Section 1-5
byJimbo Lamb
 
PDF
Geometry Section 1-4
byJimbo Lamb
 
PDF
Geometry Section 4-6 1112
byJimbo Lamb
 
PDF
trigonometry
byWeerachat Martluplao
 
PDF
Geometry Section 4-2
byJimbo Lamb
 
PDF
Geometry Section 1-2
byJimbo Lamb
 
PDF
Geometry Section 1-3 1112
byJimbo Lamb
 
Geometry Section 1-2
byJimbo Lamb
 
Geometry Section 1-5
byJimbo Lamb
 
Geometry Section 1-4
byJimbo Lamb
 
Geometry Section 4-6 1112
byJimbo Lamb
 
trigonometry
byWeerachat Martluplao
 
Geometry Section 4-2
byJimbo Lamb
 
Geometry Section 1-2
byJimbo Lamb
 
Geometry Section 1-3 1112
byJimbo Lamb
 

What's hot

PPTX
Chapter 8 Study Guide
bywzuri
 
PPTX
Gcse volumes surfaceareaofsolids
bytylerj251201
 
PDF
Module 3 similarity
bydionesioable
 
PPT
Three dimensional geometry
byAnthony_Maiorano
 
PDF
Module 2 similarity
bydionesioable
 
PDF
Module 1 similarity
byDanica Balilla
 
PPTX
Instrumentation in mathematics (Instructional Materials)
byLara Katrina
 
PDF
Module 2 properties of quadrilaterals
bydionesioable
 
PPT
Instructional Materials in Mathematics
byMary Caryl Yaun
 
PDF
Geometry Section 6-2
byJimbo Lamb
 
PPTX
Instrumentation in Mathematics
byFate Jacaban
 
DOC
Guide de problem solving avec solution - préparation entretiens conseil
byJocelyne Giambiaggi
 
PDF
Geometry Section 6-5
byJimbo Lamb
 
PPTX
Instrumentation in mathematics
byCarina Ancheta
 
PPTX
The Pythagorean Theorem
byFidelfo Moral
 
ODP
Aptitude test papers
byDr. Trilok Kumar Jain
 
PPTX
(7) Lesson 8.2
bywzuri
 
PPT
Teorema de pitágoras
bymatematico12357
 
Chapter 8 Study Guide
bywzuri
 
Gcse volumes surfaceareaofsolids
bytylerj251201
 
Module 3 similarity
bydionesioable
 
Three dimensional geometry
byAnthony_Maiorano
 
Module 2 similarity
bydionesioable
 
Module 1 similarity
byDanica Balilla
 
Instrumentation in mathematics (Instructional Materials)
byLara Katrina
 
Module 2 properties of quadrilaterals
bydionesioable
 
Instructional Materials in Mathematics
byMary Caryl Yaun
 
Geometry Section 6-2
byJimbo Lamb
 
Instrumentation in Mathematics
byFate Jacaban
 
Guide de problem solving avec solution - préparation entretiens conseil
byJocelyne Giambiaggi
 
Geometry Section 6-5
byJimbo Lamb
 
Instrumentation in mathematics
byCarina Ancheta
 
The Pythagorean Theorem
byFidelfo Moral
 
Aptitude test papers
byDr. Trilok Kumar Jain
 
(7) Lesson 8.2
bywzuri
 
Teorema de pitágoras
bymatematico12357
 

Similar to Pythagoras Theorem Graphs

PPTX
Pythagoras-Finding-C-Complete-Lesson.pptx
bymuekshmalani
 
PPT
March 23-March 27
byjschendel
 
PDF
pytagoras theorem.pdf
byRedzOne18
 
PPTX
Pythagorean theorem-and-special-right-triangles
byCharmaine Garridos
 
PPTX
Pythagorean Theorem
byEdrin Jay Morta
 
PPTX
Ppt for geometry
byNatalie Gan
 
PDF
Area of 2 dimensional figures (circle, square etc)
byjaniva1
 
PDF
Pythagorean Clues Worksheet
byjacob_lingley
 
PDF
Pythagoras' Theorem & Square root pptttt
bystephanieshum7
 
PDF
Pythagoras packet 3
byTed Hughes
 
PDF
Similarity (2010 2018) paper4
byOnekai
 
PPTX
11.4 pythagorean theorem day 1
bybweldon
 
PPTX
Pythagorean theorem 11.4
bybweldon
 
PPTX
Deeps
byepsyba
 
PPT
Chapter4.9
bynglaze10
 
PDF
Mod_01_Maths_Questions.pdf
byssuserb8f6881
 
PPTX
Introduction to Pythagoras’ Theorem Lesson
byapol10
 
PPT
Geometry unit 8.1
byMark Ryder
 
PPTX
(8) Lesson 5.5 - The Pythagorean Theorem
bywzuri
 
PPT
Core sub math_att_4pythagoreantheorem
bySatyam Gupta
 
Pythagoras-Finding-C-Complete-Lesson.pptx
bymuekshmalani
 
March 23-March 27
byjschendel
 
pytagoras theorem.pdf
byRedzOne18
 
Pythagorean theorem-and-special-right-triangles
byCharmaine Garridos
 
Pythagorean Theorem
byEdrin Jay Morta
 
Ppt for geometry
byNatalie Gan
 
Area of 2 dimensional figures (circle, square etc)
byjaniva1
 
Pythagorean Clues Worksheet
byjacob_lingley
 
Pythagoras' Theorem & Square root pptttt
bystephanieshum7
 
Pythagoras packet 3
byTed Hughes
 
Similarity (2010 2018) paper4
byOnekai
 
11.4 pythagorean theorem day 1
bybweldon
 
Pythagorean theorem 11.4
bybweldon
 
Deeps
byepsyba
 
Chapter4.9
bynglaze10
 
Mod_01_Maths_Questions.pdf
byssuserb8f6881
 
Introduction to Pythagoras’ Theorem Lesson
byapol10
 
Geometry unit 8.1
byMark Ryder
 
(8) Lesson 5.5 - The Pythagorean Theorem
bywzuri
 
Core sub math_att_4pythagoreantheorem
bySatyam Gupta
 

More from LiveOnlineClassesInd

PPTX
1th physics-laws of motion-force and inertia
byLiveOnlineClassesInd
 
PPTX
9th igcse-physics-moments of force
byLiveOnlineClassesInd
 
PPTX
Narrative
byLiveOnlineClassesInd
 
PPTX
12th CBSE - Biomolecules
byLiveOnlineClassesInd
 
PPTX
11. 7th CBSE - Transportation in Plants and Animals
byLiveOnlineClassesInd
 
PPTX
7th Maths - Properties Of Rational Numbers
byLiveOnlineClassesInd
 
PPTX
7th icse - biology - Nutrition in Animals and Plants
byLiveOnlineClassesInd
 
PPTX
12th Cbse - Biomolecules
byLiveOnlineClassesInd
 
PPTX
9th- Why Do We Fall Ill - Cbse - Biology
byLiveOnlineClassesInd
 
PPTX
Year 8 -Term 2- Unit 4 - Lesson 3- Neutralization
byLiveOnlineClassesInd
 
PPTX
Electrochemistry - CBSE
byLiveOnlineClassesInd
 
PDF
Informal Letter
byLiveOnlineClassesInd
 
PDF
7th Modal Verb Part 2
byLiveOnlineClassesInd
 
PPTX
Interjections
byLiveOnlineClassesInd
 
PPTX
8th article writing
byLiveOnlineClassesInd
 
PPTX
Narrative
byLiveOnlineClassesInd
 
PDF
7th-Modal Verb Part 2 CBSE
byLiveOnlineClassesInd
 
PPTX
10 TH - Life Process - cbse - biology
byLiveOnlineClassesInd
 
PPTX
7th Modals Verbs Cbse
byLiveOnlineClassesInd
 
PPTX
11th physics-motion in a straight line-frame of reference
byLiveOnlineClassesInd
 
1th physics-laws of motion-force and inertia
byLiveOnlineClassesInd
 
9th igcse-physics-moments of force
byLiveOnlineClassesInd
 
Narrative
byLiveOnlineClassesInd
 
12th CBSE - Biomolecules
byLiveOnlineClassesInd
 
11. 7th CBSE - Transportation in Plants and Animals
byLiveOnlineClassesInd
 
7th Maths - Properties Of Rational Numbers
byLiveOnlineClassesInd
 
7th icse - biology - Nutrition in Animals and Plants
byLiveOnlineClassesInd
 
12th Cbse - Biomolecules
byLiveOnlineClassesInd
 
9th- Why Do We Fall Ill - Cbse - Biology
byLiveOnlineClassesInd
 
Year 8 -Term 2- Unit 4 - Lesson 3- Neutralization
byLiveOnlineClassesInd
 
Electrochemistry - CBSE
byLiveOnlineClassesInd
 
Informal Letter
byLiveOnlineClassesInd
 
7th Modal Verb Part 2
byLiveOnlineClassesInd
 
Interjections
byLiveOnlineClassesInd
 
8th article writing
byLiveOnlineClassesInd
 
Narrative
byLiveOnlineClassesInd
 
7th-Modal Verb Part 2 CBSE
byLiveOnlineClassesInd
 
10 TH - Life Process - cbse - biology
byLiveOnlineClassesInd
 
7th Modals Verbs Cbse
byLiveOnlineClassesInd
 
11th physics-motion in a straight line-frame of reference
byLiveOnlineClassesInd
 

Recently uploaded

PDF
Radio Ceylon Finals (An Indian Subcontinent Quiz).pdf
byConquiztadors- the Quiz Society of Sri Venkateswara College
 
PPTX
Master of Punjabi Short Story "kartar singh duggal
bybhautikbharwad4
 
PPTX
West Hatch High School: Year 9 Art Course
byWestHatch
 
PPTX
West Hatch High School - GCSE Art Presentation
byWestHatch
 
PPTX
West Hatch High School -- GCSE Geography
byWestHatch
 
PDF
Schrodinger's Capital Finals (SciBiz Quiz).pdf
byConquiztadors- the Quiz Society of Sri Venkateswara College
 
PPTX
That long silence - Novel by Shashi Deshapande
bysanjanavaghela65
 
PPTX
literary theory and criticism by Vivek p
byvivekrathodborda
 
PPTX
Toba Tek Singh - Visualising Partition through Manto's Lens
bymiraljoshi48
 
PDF
Sharad Bisen_Irrigation Systems and Methods in Horticultural Crops.pdf
bybisensharad
 
PDF
Q4_LE_English 5_Lesson 1_Week 1.pdf learning instruction
byMichelleCajefe2
 
PPTX
How to Track Team Performance Analysis in Odoo 18 Recruitment
byCeline George
 
PPTX
Biological source, chemical constituents, and therapeutic efficacy of the fol...
bySai Meer College of Pharmacy
 
PPTX
"Aristotle : Father Of Western Philosophy"
bymitalbarathod28
 
PPTX
West Hatch High School - GCSE Media Studies
byWestHatch
 
PPT
West Hatch High School - GCSE History Option
byWestHatch
 
PPTX
How Physician Assistants in the USA Earn CME Credits Online.pptx
byCME4Life
 
PPTX
Reimagining Academic Library Services through Artificial Intelligence: A Case...
byDon Bosco College, Itanagar
 
PDF
Chapter 05 Drug Acting on CNS General Anasthetics.pdf
bySandeshSul
 
PPTX
Central Line Associated Bloodstream Infection
bynabinabhaila40
 
Radio Ceylon Finals (An Indian Subcontinent Quiz).pdf
byConquiztadors- the Quiz Society of Sri Venkateswara College
 
Master of Punjabi Short Story "kartar singh duggal
bybhautikbharwad4
 
West Hatch High School: Year 9 Art Course
byWestHatch
 
West Hatch High School - GCSE Art Presentation
byWestHatch
 
West Hatch High School -- GCSE Geography
byWestHatch
 
Schrodinger's Capital Finals (SciBiz Quiz).pdf
byConquiztadors- the Quiz Society of Sri Venkateswara College
 
That long silence - Novel by Shashi Deshapande
bysanjanavaghela65
 
literary theory and criticism by Vivek p
byvivekrathodborda
 
Toba Tek Singh - Visualising Partition through Manto's Lens
bymiraljoshi48
 
Sharad Bisen_Irrigation Systems and Methods in Horticultural Crops.pdf
bybisensharad
 
Q4_LE_English 5_Lesson 1_Week 1.pdf learning instruction
byMichelleCajefe2
 
How to Track Team Performance Analysis in Odoo 18 Recruitment
byCeline George
 
Biological source, chemical constituents, and therapeutic efficacy of the fol...
bySai Meer College of Pharmacy
 
"Aristotle : Father Of Western Philosophy"
bymitalbarathod28
 
West Hatch High School - GCSE Media Studies
byWestHatch
 
West Hatch High School - GCSE History Option
byWestHatch
 
How Physician Assistants in the USA Earn CME Credits Online.pptx
byCME4Life
 
Reimagining Academic Library Services through Artificial Intelligence: A Case...
byDon Bosco College, Itanagar
 
Chapter 05 Drug Acting on CNS General Anasthetics.pdf
bySandeshSul
 
Central Line Associated Bloodstream Infection
bynabinabhaila40
 

Pythagoras Theorem Graphs

  • 1.
    How can weapply Pythagoras’ Theorem in graphs and other triangles? Learning Objective
  • 2.
    • To reviseall parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes Learning Outcomes
  • 3.
    To find cuse: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a _________________:
  • 4.
    To find cuse: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a _________________:
  • 5.
    To find cuse: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a _________________:
  • 6.
    To find cuse: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a _________________:
  • 7.
    To find cuse: 𝑐2 = ℎ2 − 𝑏² To find b use: 𝑏2 = ℎ2 − 𝑐² To find the hypotenuse, we use: ℎ² = 𝑏² + 𝑐² The Theorem only works on a right angle triangle:
  • 8.
    Learning Outcomes • Torevise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
  • 9.
    Learning Outcomes • Torevise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
  • 10.
  • 11.
    Edexel Pythagoras Question Weuse Pythagoras’ Theorem to calculate the distance between Norwich and York.
  • 12.
    Edexel Pythagoras Question Weuse Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 =?2 +?2
  • 13.
    Edexel Pythagoras Question Weuse Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 =?2 +?2 b c
  • 14.
    Edexel Pythagoras Question Weuse Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 b c
  • 15.
    Edexel Pythagoras Question Weuse Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 ℎ2 = 1682 + 1572 b c
  • 16.
    Edexel Pythagoras Question Weuse Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 ℎ2 = 1682 + 1572 ℎ2 = 52873 b c
  • 17.
    Edexel Pythagoras Question Weuse Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 ℎ2 = 1682 + 1572 ℎ2 = 52873 ℎ = 52873 b c
  • 18.
    Edexel Pythagoras Question Weuse Pythagoras’ Theorem to calculate the distance between Norwich and York. The Hypotenuse is the distance between them: ℎ2 = 𝑏2 + 𝑐2 ℎ2 = 1682 + 1572 ℎ2 = 52873 ℎ = 52873 ℎ = 229.94𝑘𝑚 (𝑡. 2. 𝑑. 𝑝) b c
  • 20.
    𝑏2 = ℎ2− 𝑐2 𝑥
  • 21.
    𝑏2 = ℎ2− 𝑐2 𝑥2 = 62 − 22 𝑥
  • 22.
    𝑏2 = ℎ2− 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥
  • 23.
    𝑏2 = ℎ2− 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥2 = 34 𝑥
  • 24.
    𝑏2 = ℎ2− 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥2 = 34 𝑥 = 34 𝑥
  • 25.
    𝑏2 = ℎ2− 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥2 = 34 𝑥 = 34 𝑥 = 5.65685 … 𝑥
  • 26.
    𝑏2 = ℎ2− 𝑐2 𝑥2 = 62 − 22 𝑥2 = 36 − 4 𝑥2 = 34 𝑥 = 34 𝑥 = 5.65685 … The perpendicular height of the triangle is 5.7cm to 1 decimal place. 𝑥
  • 27.
    Pythagoras – Nonright angled triangle 𝑥
  • 28.
    𝑥² + 2²= 4² Pythagoras – Non right angled triangle 𝑥
  • 29.
    𝑥² + 2²= 4² 𝑥² = 4² - 2² Pythagoras – Non right angled triangle 𝑥
  • 30.
    𝑥² + 2²= 4² 𝑥² = 4² - 2² 𝑥² = 16 - 4 Pythagoras – Non right angled triangle 𝑥
  • 31.
    𝑥² + 2²= 4² 𝑥² = 4² - 2² 𝑥² = 16 – 4 𝑥 = 12 Pythagoras – Non right angled triangle 𝑥
  • 32.
    𝑥² + 2²= 4² 𝑥² = 4² - 2² 𝑥² = 16 – 4 𝑥 = 12 𝑥 = 3.5cm (1.d.p) Pythagoras – Non right angled triangle 𝑥
  • 33.
    a) Calculate thelength of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. Examination Questions
  • 34.
    a) Calculate thelength of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 Examination Questions
  • 35.
    a) Calculate thelength of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = √52 = 7.211102551 Examination Questions
  • 36.
    a) Calculate thelength of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm Examination Questions
  • 37.
    a) Calculate thelength of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm b) Area = ½ x 4 x 6 Examination Questions
  • 38.
    a) Calculate thelength of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm b) Area = ½ x 4 x 6 = 12 cm² Examination Questions
  • 39.
    a) Calculate thelength of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm b) Area = ½ x 4 x 6 = 12 cm² c) P = 4 + 6 + 7.211102551 Examination Questions
  • 40.
    a) Calculate thelength of AC giving your answer correct to 3 significant figures. b) Calculate the area of triangle ABC. c) Calculate the perimeter of triangle ABC giving your answer correct to 1 decimal place. a) AC² = 4² + 6² = 52 AC = 52 = 7.211102551 AC = 7.21 cm b) Area = ½ x 4 x 6 = 12 cm² c) P = 4 + 6 + 7.211102551 = 17.2 cm Examination Questions
  • 41.
  • 42.
    • V =Area of the cross section x depth Examination Questions
  • 43.
    • V =Area of the cross section x depth. • We need to find the area of the cross section. Examination Questions
  • 44.
    • V =Area of the cross section x depth. • We need to find the area of the cross section. • It’s a triangle!!! Examination Questions
  • 45.
    • V =Area of the cross section x depth. • We need to find the area of the cross section. • It’s a triangle!!! • Area = ½ (Base x Height) • We need to calculate the height Examination Questions
  • 46.
    • V =Area of the cross section x depth. • We need to find the area of the cross section. • It’s a triangle!!! • Area = ½ (Base x Height) • We need to calculate the height Height : we know the longest side and the base. Examination Questions
  • 47.
    • Pythagoras • a²= b² + c² • 5.3² = 2.8²+c² • c² = 5.3²-2.8² • = 20.25 • c = 20.25 • = 4.5 Height : we know the longest side and the base. Examination Questions
  • 48.
    • Volume We nowneed to put the answer into the Volume formula. Examination Questions
  • 49.
    • Volume • V= ½(4.5x2.8) x 3.5 We now need to put the answer in to the Volume formula. Examination Questions
  • 50.
    • Volume • V= ½(4.5x2.8) x 3.5 • = ½(12.6) x 3.5 • = 6.3 x 3.5 • = 22.05cm³ We now need to put the answer in to the Volume formula. Examination Questions
  • 51.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. Examination Questions
  • 52.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. Examination Questions
  • 53.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. Examination Questions
  • 54.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! Examination Questions
  • 55.
    First we needto find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. Examination Questions
  • 56.
    First we needto find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? This is a representation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. Examination Questions
  • 57.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: Examination Questions
  • 58.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² Examination Questions
  • 59.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² Examination Questions
  • 60.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Examination Questions
  • 61.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 Examination Questions
  • 62.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 = 16064.2cm³ Examination Questions
  • 63.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 = 16064.2cm³ Not there yet! Now we calculate the litres 1cm³ = 1ml, 1000 ml = 1L Examination Questions
  • 64.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 = 16064.2cm³ Not there yet! Now we calculate the litres 1cm³ = 1ml, 1000 ml = 1L Hence: 16064.2 ÷ 1000 = Examination Questions
  • 65.
    This is arepresentation of a water tank. For every 1cm³ there is 1ml. Calculate how many litres of water would the tank hold. First we need to find the area of the cross section. That means finding the width and the length. We don’t know the Length!!!! To find the width we use Pythagoras’ Theorem! Which side do I need to find? ONE OF THE SHORTER SIDES So we use: b² = a² - c² = 24.7² - 16.3² b = 18.56cm (2dp) Now we use the Volume formula Vol = Width x Length x Depth = 18.56 x 16.3 x 53.1 = 16064.2cm³ Not there yet! Now we calculate the litres 1cm³ = 1ml, 1000 ml = 1L Hence: 16064.2 ÷ 1000 = 16.06L (2dp) Examination Questions
  • 66.
    Learning Outcomes • Torevise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
  • 67.
    Learning Outcomes • Torevise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
  • 68.
    We can alsouse Pythagoras’ Theorem to calculate the length of a diagonal line on a graph. Pythagoras on a Graph
  • 69.
    We can alsouse Pythagoras’ Theorem to calculate the length of a diagonal line on a graph. P1: (1,3) P2: (7,8) Pythagoras on a Graph
  • 70.
    We can alsouse Pythagoras’ Theorem to calculate the length of a diagonal line on a graph. P1: (1,3) P2: (7,8) Use the co-ordinates to find the horizontal and vertical difference between the two points. Pythagoras on a Graph
  • 71.
    P1: (1,3) P2: (7,8) Vertical= y2 – y1 Horizontal = x2 – x1 Pythagoras on a Graph
  • 72.
    P1: (1,3) P2: (7,8) Vertical= 8 – 3 Horizontal = 7 – 1 Pythagoras on a Graph
  • 73.
    P1: (1,3) P2: (7,8) Vertical= 8 – 3 Horizontal = 7 – 1 Pythagoras on a Graph
  • 74.
    P1: (1,3) P2: (7,8) Vertical= 8 – 3 = 5 Horizontal = 7 – 1 = 6 Pythagoras on a Graph
  • 75.
    P1: (1,3) P2: (7,8) Vertical= 8 – 3 = 5 Horizontal = 7 – 1 = 6 Now we can use Pythagoras’ Theorem. Pythagoras on a Graph
  • 76.
    P1: (1,3) P2: (7,8) Vertical= 8 – 3 = 5 Horizontal = 7 – 1 = 6 Now we can use Pythagoras’ Theorem. P1P2² = 5² + 6² Pythagoras on a Graph
  • 77.
    P1: (1,3) P2: (7,8) Vertical= 8 – 3 = 5 Horizontal = 7 – 1 = 6 Now we can use Pythagoras’ Theorem. P1P2² = 5² + 6² P1P2 = 61 = Pythagoras on a Graph
  • 78.
    P1: (1,3) P2: (7,8) Vertical= 8 – 3 = 5 Horizontal = 7 – 1 = 6 Now we can use Pythagoras’ Theorem. P1P2² = 5² + 6² P1P2 = 61 = 7.81cm (2dp) Pythagoras on a Graph
  • 79.
    The distance betweenthe points A(x1, y1) and B(x2, y2) is ( ) ( ) x x y y   2 2 2 1 2 1 + Pythagoras on a Graph
  • 80.
    The distance betweenthe points A(x1, y1) and B(x2, y2) is ( ) ( ) x x y y   2 2 2 1 2 1 + P1 = (4,7) P2 = (5,3) Distance = 5 − 4 2 + (3 − 7)² Pythagoras on a Graph
  • 81.
    The distance betweenthe points A(x1, y1) and B(x2, y2) is ( ) ( ) x x y y   2 2 2 1 2 1 + P1 = (4,7) P2 = (5,3) Distance = 5 − 4 2 + (3 − 7)² = 1 + 16 Pythagoras on a Graph
  • 82.
    The distance betweenthe points A(x1, y1) and B(x2, y2) is ( ) ( ) x x y y   2 2 2 1 2 1 + P1 = (4,7) P2 = (5,3) Distance = 5 − 4 2 + (3 − 7)² = 17 = 4.12cm (2.d.p) Pythagoras on a Graph
  • 83.
  • 84.
    P1 = (3,2)P2 = (9,7) Distance = 9 − 3 2 + (7 − 2)² = = Pythagoras on a Graph
  • 85.
    P1 = (3,2)P2 = (9,7) Distance = 9 − 3 2 + (7 − 2)² = 36 + 25 = Pythagoras on a Graph
  • 86.
    P1 = (3,2)P2 = (9,7) Distance = 9 − 3 2 + (7 − 2)² = 61 = Pythagoras on a Graph
  • 87.
    P1 = (3,2)P2 = (9,7) Distance = 9 − 3 2 + (7 − 2)² = 61 = 7.81cm (2.d.p) Pythagoras on a Graph
  • 88.
  • 89.
    P1 = (4,-4)P2 = (-5,3) Distance = = = Pythagoras on a Graph
  • 90.
    P1 = (4,-4)P2 = (-5,3) Distance = −5 − 4 2 + (3 − −4)² = = Pythagoras on a Graph
  • 91.
    P1 = (4,-4)P2 = (-5,3) Distance = −5 − 4 2 + (3 − −4)² = −9 ² + 7² = Pythagoras on a Graph
  • 92.
    P1 = (4,-4)P2 = (-5,3) Distance = −5 − 4 2 + (3 − −4)² = 130 = Pythagoras on a Graph
  • 93.
    P1 = (4,-4)P2 = (-5,3) Distance = −5 − 4 2 + (3 − −4)² = 130 = 11.40cm (2.d.p) Pythagoras on a Graph
  • 94.
    P1 = P2= Distance = = = Pythagoras on a Graph
  • 95.
    P1 = (4,-4)P2 = (2,5) Distance = 2 − 4 2 + (5 − −4)² = = Pythagoras on a Graph
  • 96.
    P1 = (4,-4)P2 = (2,5) Distance = 2 − 4 2 + (5 − −4)² = 4 + 81 = Pythagoras on a Graph
  • 97.
    P1 = (4,-4)P2 = (2,5) Distance = 2 − 4 2 + (5 − −4)² = 85 = Pythagoras on a Graph
  • 98.
    Pythagoras on aGraph P1 = (4,-4) P2 = (2,5) Distance = 2 − 4 2 + (5 − −4)² = 85 = 9.21cm (2.d.p)
  • 99.
    Learning Outcomes • Torevise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes
  • 100.
    Learning Outcomes • Torevise all parts of the theorem • To calculate the length of one of the sides • To devise a way to use the Theorem in 3D shapes

Editor's Notes

  • #2 An overview of the content of the lesson Must be in the form of a question where appropriate Students should be able to answer the question at the end - either fully, partly or in a way that demonstrates they understand what gaps in their knowledge they need to address Verbs such as to understand / to know / to gain confidence / to learn Ask students to give the question a go and point out that, at the end of the lesson, they should be able to answer fully
  • #3 Measureable outcomes that students can demonstrate and self-assess against Must be written using Bloom’s taxonomy verbs Verbs based on students ability and pitch of lesson It must be clear that students understand the outcomes before moving on Make an activity of this slide: Ask students to read this aloud Ask them to paraphrase Ask that they explain what they mean Ask what they already know related to these outcomes There may be as few as 2 outcomes, or max 4
  • #9 Revisit the first outcome and use the polling function to allow students to privately self-assess You may feel that the students do not need privacy to self-assess and in this instance, the chat box may be used Polling must be used until you can fully assess their confidence to use the chat box and express honesty If students self-assess as a 4/5, ensure that you are fully confident in their assessment Ask questions Ask for examples Students to ask each other questions If a few students self-assesses as a 3, but others as a 4/5, discretely ask the higher ones to give examples and to explain their achievement/understanding If all students are a 3 or below, do not move on. Move to a blank page at the end of the presentation and use as a whiteboard to further explain If students are ½, go back to the beginning Always ask students what the gaps are and help them to identify these in order to promote metacognition
  • #10 1. The outcome changes colour when achieved to the same colour as the objective to demonstrate the connection, progress and what happens next
  • #67 1. The outcome changes colour when achieved to the same colour as the objective to demonstrate the connection, progress and what happens next
  • #68 1. The outcome changes colour when achieved to the same colour as the objective to demonstrate the connection, progress and what happens next
  • #69 Explanation and use the writing pad.
  • #70 Explanation and use the writing pad.
  • #71 Explanation and use the writing pad.
  • #72 Explanation and use the writing pad.
  • #73 Explanation and use the writing pad.
  • #74 Explanation and use the writing pad.
  • #75 Explanation and use the writing pad.
  • #76 Explanation and use the writing pad.
  • #77 Explanation and use the writing pad.
  • #78 Explanation and use the writing pad.
  • #79 Explanation and use the writing pad.
  • #80 Explanation and use the writing pad.
  • #81 Explanation and use the writing pad.
  • #82 Explanation and use the writing pad.
  • #83 Explanation and use the writing pad.
  • #84 Explanation and use the writing pad.
  • #85 Explanation and use the writing pad.
  • #86 Explanation and use the writing pad.
  • #87 Explanation and use the writing pad.
  • #88 Explanation and use the writing pad.
  • #89 Explanation and use the writing pad.
  • #90 Explanation and use the writing pad.
  • #91 Explanation and use the writing pad.
  • #92 Explanation and use the writing pad.
  • #93 Explanation and use the writing pad.
  • #94 Explanation and use the writing pad.
  • #95 Explanation and use the writing pad.
  • #96 Explanation and use the writing pad.
  • #97 Explanation and use the writing pad.
  • #98 Explanation and use the writing pad.
  • #99 Explanation and use the writing pad.
  • #100 1. The outcome changes colour when achieved to the same colour as the objective to demonstrate the connection, progress and what happens next
  • #101 1. The outcome changes colour when achieved to the same colour as the objective to demonstrate the connection, progress and what happens next