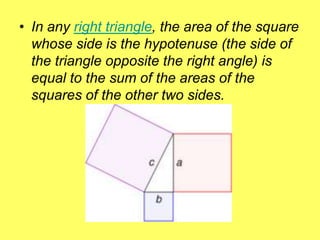
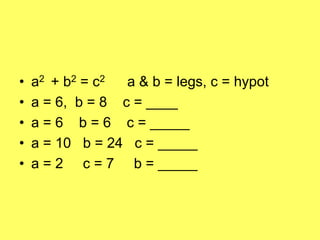Here are the steps to solve problems 1-15 and 35 from page 740 of the textbook using the Pythagorean theorem: 1. Identify the formula: a^2 + b^2 = c^2 2. Substitute the given values for a, b, and c into the formula 3. Simplify by combining like terms 4. Solve for the unknown side length by taking the square root of each side 5. Round your answer to the nearest tenth if instructed to do so Be sure to show the setup and work for each problem. Label answers clearly. Bring any questions to class tomorrow.

1. Pythagorean Theorem
Section 11.4
P. 737

2. • Pythagoras was born around 570 BC on the island of Samos
in ancient Greece.
• That is about 2,570 years ago!

3. Pythagoras
• He founded a school in southern Italy after
traveling in Egypt and the Middle East. He
was a philosopher, musician, and
astronomer, but he is most remembered
as a mathematician.

4. • The Egyptians knew that a triangle with sides 3, 4, and 5
make a 90o angle. As a matter of fact, they had a rope
with 12 evenly spaced knots like this one:
•
• that they used to cut stones and build perfect corners in
their buildings and pyramids. It is believed that they only
knew about the 3, 4, 5 triangle and not the general
theorem that applies to all right triangles.

5. • In any right triangle, the area of the square
whose side is the hypotenuse (the side of
the triangle opposite the right angle) is
equal to the sum of the areas of the
squares of the other two sides.

6. • The Pythagorean Theorem is one of the
most important theorems in the whole
realm of geometry.
• When the two shorter sides in a right
triangle are squared and then added, the
sum equals the square of the longest side
or hypotenuse.

7. The Pythagorean Theorem
Where c is the length of the hypotenuse and
a and b are the lengths of the other two
sides, the theorem can be expressed as
the following equation:
• c2 – a2 = b2
• c2 – b2 = a2

8. • The Pythagorean Theorem
• If a triangle is a right triangle, then the sum
of the squares of the lengths of the legs a
and b equals the square of the length of
the hypotenuse c.
c
• a2 + b2 = c2 a
b

9. • Also true is:
c 2 - b 2 = a2
• This would be used to find one of the legs
if you know the length of the hypotenuse
and the other leg.

10. EXAMPLE 1 Use the Pythagorean theorem
Find the unknown length for the triangle shown.
SOLUTION
a 2+ b 2 = c 2 Pythagorean theorem
2
a 2 + 6 = 72 Substitute 6 for b and 7 for c.
a 2 + 36 = 49 Simplify.
a 2 = 13 Subtract 36 from each side.
a = 13 Take positive square root of each side.
ANSWER The side length a is = 13

11. GUIDED PRACTICE for Example 1
1. The lengths of the legs of a right triangle are a = 5
and b = 12. Find c.
ANSWER c = 13

12. • a2 + b2 = c2 a & b = legs, c = hypot
• a = 6, b = 8 c = ____
• a = 6 b = 6 c = _____
• a = 10 b = 24 c = _____
• a = 2 c = 7 b = _____

13. • Determine if the given lengths are sides of
a right triangle.
• 5, 11, 12
• 20, 29, 21
• 11.9, 12, 16.9

14. • Assignment: P. 740
• 1-15, 35
• Make sure you put formula / work on your
paper!
• Round to the nearest tenths.

15. P. 740 1-15, 35