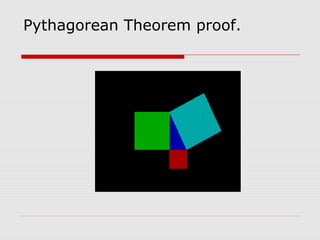
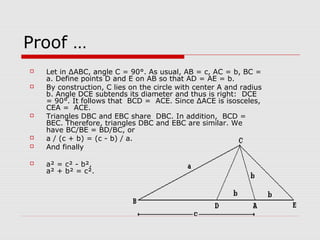
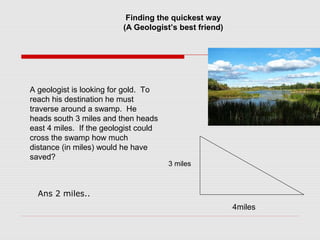
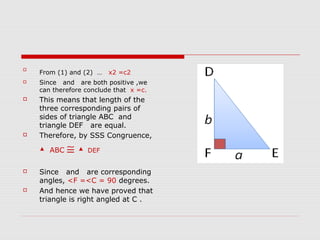
The document discusses the history and development of the Pythagorean theorem. It explains that Pythagoras founded a philosophical school in Croton, Italy, where he and his followers studied mathematics and believed that numbers were the ultimate reality. The document then provides several proofs of the Pythagorean theorem, including using similar triangles, adding the areas of shapes, and the converse theorem. It also discusses Pythagoras' contributions to music and other areas of mathematics.

1. Pythagoras

2. Hello and welcome to the adventure of discovering the
Pythagorean Theorem. The Pythagorean Theorem is one of the
greatest theorems known today. This discovery was credited to
Pythagoras of Samos. Pythagoras believed that everything was
related to mathematics and that numbers were the ultimate reality
and, through mathematics, everything could be predicted and
measured. So as you embark on your discovery remember that
great minds think alike and don’t give up no matter what the cost.

3. History of Pythagoras
 Pythagoras founded a philosophical and
religious school/society in Croton (now
spelled Crotone, in southern Italy)
 His followers were commonly referred to
as Pythagoreans.
 The members of the inner circle of the
society were called the “ mathematikoi ”
 The members of the society followed a
strict code which held them to being
vegetarians and have no personal
possessions.

4. History of Pythagoras (cont.)
 There is not much evidence of
Pythagoras and his society’s work
because they were so secretive and
kept no records .
 One major belief was that all things
in nature and all relations could be
reduced to number relations .

5. Pythagoras and Music
 Pythagoras made important developments
in music and astronomy
 Observing that plucked strings of
different lengths gave off different
tones, he came up with the musical
scale still used today.

6. Pythagoras and Math
 Pythagoras made many contributions
to the world of math including:
 Studies with even/odd numbers
 Studies involving Perfect and Prime
Numbers
 Irrational Numbers
 Various theorems/ideas about triangles,
parallel lines, circles, etc.
 Of course THE PYTHAGOREAN THEOREM

7. Proof by similar triangles.
 This proof is based on the proportionality of the
sides of two similar triangles, that is, upon the
fact that the ratio of any two corresponding
sides of similar triangles is the same regardless
of the size of the triangles.Let ABC represent a
right triangle, with the right angle located at C,
as shown on the figure. Draw the altitude from
point C, and call H its intersection with the
side AB. Point H divides the length of the
hypotenuse c into parts d and e. The new
triangle ACH is similar to triangleABC, because
they both have a right angle (by definition of
the altitude), and they share the angle at A,
meaning that the third angle will be the same in
both triangles as well, marked as θ in the
figure. By a similar reasoning,thetriangle CBH is
also similar to ABC. The proof of similarity of
the triangles requires the
 Triangle postulate: the sum of the angles in a
triangle is two right angles, and is equivalent to
theparallel postulate.
 Similarity of the triangles leads to the equality
of ratios of corresponding sides:

8. The first result equates
the cosines of the angles θ, whereas the
second result equates their sines.
 These ratios can be written as
 Summing these two equalities
results in

 which, after simplification, expresses
the Pythagorean theorem:


9. Pythagorean Theorem proof.

10. Another Proof…

11. Proof …
 Let in ΔABC, angle C = 90°. As usual, AB = c, AC = b, BC =
a. Define points D and E on AB so that AD = AE = b.
 By construction, C lies on the circle with center A and radius
b. Angle DCE subtends its diameter and thus is right: DCE
= 90°. It follows that BCD = ACE. Since ΔACE is isosceles,
CEA = ACE.
 Triangles DBC and EBC share DBC. In addition, BCD =
BEC. Therefore, triangles DBC and EBC are similar. We
have BC/BE = BD/BC, or
 a / (c + b) = (c - b) / a.
 And finally
 a² = c² - b²,
a² + b² = c².

12. Proof of the theorem…
 There are many other way to prove the
theorem but we will refer to this as our proof.
 Take a look at this diagram ... it has that
"abc”triangle in it (four of them actually):
 Now let's add up the areas of all the smaller
pieces:
 First, the smaller (tilted) square has an area
of
 A = c2 And there are four triangles, each
one has an area of
 A =½ab So all four of them combined is
 A = 4(½ab) = 2ab So, adding up the tilted
square and the 4 triangles gives:
 A = c2+2ab

13. The area of the large square is equal to the area
of the tilted square and the 4 triangles. This
can be written as:
(a+b)(a+b) = c2+2ab
NOW, let us rearrange this to see if we can get the
pythagoras theorem:
Start with: (a+b)(a+b)=c2 + 2ab
Expand (a+b)(a+b): a2 + 2ab + b2=c2 + 2ab
Subtract "2ab" from both sides:
a2 + b2 = c2

14. Discovering the distance from which ladder is to be
kept .
The tallest building in Bangalore is 356 feet.
The average height for a fire engine is 12 feet.
If the fire department is required to be 50 feet
away from the building how long (in feet) must
the ladder be to reach someone on the roof of
the tallest building? Round to two decimal
places.
The distance of the ladder is FIXED. The
distance of the burning floor is FIXED. (from
the ground.)
By using the theorem we could change the
distance between the foot of the ladder and the
foot of the building .
25 feet
24feet
Daily Life Applications
Ans. 7 feet

15. Finding the quickest way
(A Geologist’s best friend)
A geologist is looking for gold. To
reach his destination he must
traverse around a swamp. He
heads south 3 miles and then heads
east 4 miles. If the geologist could
cross the swamp how much
distance (in miles) would he have
saved?
3 miles
4miles
Ans 2 miles..

16. Converse of the
Pythagoras theorem
 In order to prove the converse of the
Pythagorean Theorem, we need to prove
that in the figure is a right angle. Now,
we discuss the proof.
 Theorem
 In a triangle with sides , and (see
figure above), if
a2 + b2 = c2 holds,
 then is a right triangle with a right angle
at C .
 Proof
 Let DEF be a triangle such that EF=a ,
DF=b and right angled at F . If we let DE=
x , since DEF is a right triangle, by the
Pythagorean Theorem
 a2 + b2 = x2 …..(1).
 But from the supposition,
 a2 + b2 = c2 (2).

17. 
From (1) and (2) … x2 =c2
 Since and are both positive ,we
can therefore conclude that x =c.
 This means that length of the
three corresponding pairs of
sides of triangle ABC and
triangle DEF are equal.
 Therefore, by SSS Congruence,
▲ ABC ≅ ▲ DEF
 Since and are corresponding
angles, <F =<C = 90 degrees.
 And hence we have proved that
triangle is right angled at C .

18.  http://www.cut-the-knot.org/pythagoras/index.shtml
 (There are more than 144 proofs on this site.)
Thank You….
Prepared by : Raneet P Sahoo.
Class X Roll no. 10