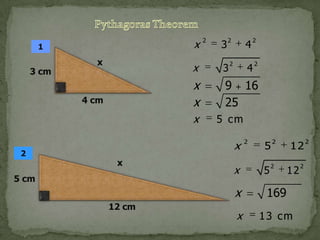
Pythagoras was an ancient Greek philosopher and mathematician born on the island of Samos in around 570 BC. He is best known for the Pythagorean theorem, which states that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. While Pythagoras likely did not discover this theorem himself, he is credited as being the first to prove why it is true. The Pythagorean theorem is one of the earliest and most important theorems in mathematics.

5. Pythagoras of Samos (Ancient Greek: Πυθαγόρας ὁ Σάμιος
[Πυθαγόρης in Ionian Greek] Pythagóras ho Sámios "Pythagoras
the Samian", or simply Πυθαγόρας; b. about 570 – d. about 495
BC)[1][2] was an Ionian Greek philosopher, mathematician, and
founder of the religious movement called Pythagoreanism. Most of
the information about Pythagoras was written down centuries after
he lived, so very little reliable information is known about him. He
was born on the island of Samos, and might have travelled widely in
his youth, visiting Egypt and other places seeking knowledge.
Around 530 BC, he moved to Croton, a Greek colony in southern
Italy, and there set up a religious sect. His followers pursued the
religious rites and practices developed by Pythagoras, and studied his
philosophical theories. The society took an active role in the politics
of Croton, but this eventually led to their downfall. The Pythagorean
meeting-places were burned, and Pythagoras was forced to flee the
city. He is said to have ended his days in Metapontum.

6. Pythagoras made influential contributions to philosophy and
religious teaching in the late 6th century BC. He is often revered
as a great mathematician, mystic and scientist, but he is best
known for the Pythagorean theorem which bears his name.
However, because legend and obfuscation cloud his work even
more than that of the other pre-Socratic philosophers, one can
give only a tentative account of his teachings, and some have
questioned whether he contributed much
to mathematics and natural philosophy. Many of the
accomplishments credited to Pythagoras may actually have been
accomplishments of his colleagues and successors. Whether or
not his disciples believed that everything was related to
mathematics and that numbers were the ultimate reality is
unknown. It was said that he was the first man to call himself a
philosopher, or lover of wisdom,[3] and Pythagorean ideas
exercised a marked influence on Plato, and through him, all
of Western philosophy.

7. Pythagoras made many contributions to
Mathematics and Physics but the contribution that
we will be exploring is: The Pythagorean Theorem.
The Pythagorean Theorem is a formula that can be
used only when working with right triangles. It can
help you find the length of any side of a right
triangle. Pythagoras wasn't the first to discover this
formula. The Babylonians and the Chinese worked
with this concept years before Pythagoras.
Pythagoras gets most of the credit for it though
because he was the first to prove why it works.
Several other proofs came about after his.

8. The Pythagorean Theorem was one of the earliest theorems known to ancient civilizations.
This famous theorem is named for the Greek mathematician
and philosopher, Pythagoras. Pythagoras founded the Pythagorean School of Mathematics
in Cortona, a Greek seaport in Southern Italy
. He is credited with many contributions to mathematics although some of them may have
actually been the work of his students.
The Pythagorean Theorem is Pythagoras' most famous mathematical contribution.
According to legend, Pythagoras was so happy when he
discovered the theorem that he offered a sacrifice of oxen. The later discovery that the
square root of 2 is irrational and therefore, cannot be expressed as a ratio of two
integers, greatly troubled Pythagoras and his followers. They were devout in their belief
that any two lengths were integral multiples of some unit length. Many attempts were
made to suppress the knowledge that the square root of 2 is irrational. It is even said that
the man who divulged the secret was drowned at sea. "The area of the square built upon
the hypotenuse of a right triangle is equal to the sum of the areas of the squares upon
the remaining sides."

9. Reminder of square numbers:
12 =
1x1=
1
22 =
2x2=
4
32 =
3x3=
9
42 =
4x4=
16
Index number
32
Base number
The index number tells us how
many times the base number
is multiplied by itself.
e.g. 34 means 3 x 3 x 3 x 3 = 81
1,4,9,16, …. are the answers to a number being squared so they
are called square numbers.

10. "Pythagoras' Theorem" can
be written in one short
equation:
a2 + b2 = c2
Definition
The longest side of the triangle is
called the "hypotenuse", so the
formal definition is:
In a right angled triangle:
the square of the hypotenuse is
equal to
the sum of the squares of the other
two sides.
Note:
c is the longest side of the
triangle
a and b are the other two
sides

11. Sure ... ?
Let's see if it really works using an
example.
Example: A "3,4,5" triangle has a
right angle in it.
Let's check if the areas
are the same:
32 + 42 = 52
Calculating this
becomes:
9 + 16 = 25
It works ... like Magic!

12. Why Is This Useful?
If we know the lengths of two sides of a
right angled triangle, we can find the length
of the third side. (But remember it only
works on right angled triangles!)
It works the other way around, too: when the
three sides of a triangle make a2 + b2 =
c2, then the triangle is right angled.
Example: Does this triangle have a Right Angle?
Does a2 + b2 = c2 ?
a2 + b2 = 102 + 242 =
100 + 576 = 676
c2 = 262 = 676
They are equal, so ...
Yes, it does have a Right
Angle!
Example: Does an 8, 15, 16
triangle have a Right
Angle?
Does 82 + 152 = 162 ?
82 + 152 = 64 + 225 = 289,
but 162 = 256
So, NO, it does not have a
Right Angle

13. means think what is multiplied by itself to
make this number?
Square root
Answer these questions:
1
1
4
2
9
3
16
4
49
7
Use your calculator to answer
these questions:
5 .8
2.408
25 . 4
5.040
169
13
400
20
1 21
11
1 00
10
31.623
8100
81
1000
90
225
15
361
19

14. Cut the squares
away from the right
angle triangle and cut
up the segments
of square ‘a’
q
To show how this works:
b
Draw line segment
, parallel with the
hypotenuse of the
triangle
a
x
Draw line segment
pq, at right angles to
Line segment xy.
y
p

15. Now rearrange them
to look like this.
You can see that they
make a square with
length of side ‘c’.
This demonstrates that
the areas of squares
a and b
add up to be the
area of square c
a +b
2
2
=c
2

16. x
1
3 cm
x
3
2
2
4
2
4
2
x
3
x
x
4 cm
9 + 16
25
x
2
2
5 cm
x
x
2
5
2
2
12
12 cm
5
x
5 cm
x
169
x
13 cm
12
2
2

17. x
x
2
11
2
9
5
x
2
9
11m
x
xm
11
x
23.8 cm
2
xm
7
x
x
3.4 cm
x
7.1 cm
x cm
x
2
11
2
11
23.8
2
2
21.1 cm (1 dp)
2
7.1
2
3.4
2
2
3.4
2
7.1
7
2
25
7
24 m
2
25 m
23.8
x
11 cm
2
xm
6.3 m (1 dp)
9m
6
8
2
25
2
x
x
2
Now do these:
2
7.9 cm (1 dp)
7m

18. The first proof begins with a rectangle divided up into
three triangles, each of which contains a right angle.
This proof can be seen through the use of computer
technology, or with something as simple as a 3x5 index
card cut up into right triangles
.

19. The next proof is another proof of the Pythagorean Theorem that begins with a
rectangle. It begins by constructing rectangle CADE with BA = DA. Next, we
construct the angle bisector of <BAD and let it intersect ED at point F. Thus, <BAF
is congruent to <DAF, AF = AF, and BA = DA. So, by SAS, triangle BAF = triangle DAF.
Since <ADF is a right angle, <ABF is also a right angle.
Next, since m<EBF + m<ABC + m<ABF =
180 degrees and m<ABF = 90 degrees,
<EBF and <ABC are complementary. Thus,
m<EBF + m<ABC = 90 degrees. We also
know that
m<BAC + m<ABC + m<ACB = 180 degrees.
Since m<ACB = 90 degrees, m<BAC +
m<ABC = 90 degrees. Therefore, m<EBF +
m<ABC = m<BAC + m<ABC and m<BAC =
m<EBF.
By the AA similarity theorem, triangle EBF is
similar to triangle CAB.

20. Now, let k be the similarity ratio between triangles EBF and
CAB.
.
Thus, triangle EBF has sides with
lengths ka, kb, and kc. Since FB = FD,
FD = kc. Also, since the opposite sides
of a rectangle are congruent, b = ka +
kc and c = a + kb. By solving for k, we
have
Thus,
By cross-multiplication,
Therefore,
and we have completed
the proof.

21. The next proof of the Pythagorean Theorem that will be presented is one that begins
with a right triangle. In the next figure, triangle ABC is a right triangle. Its right angle is
angle C.
Next, draw CD perpendicular to AB as shown in the next figure.
From Figures with CD, we have that (p + q) = c. By substitution, we get

22. The next proof of the Pythagorean Theorem that will be presented is one in which
a trapezoid will be used.
By the construction that was used to form this trapezoid,
all 6 of the triangles contained in this trapezoid are right
triangles. Thus,
Area of Trapezoid = The Sum of the areas of the 6
Triangles
And by using the respective formulas for area, we get:
We have completed the proof of the Pythagorean Theorem using the
trapezoid.

23. A boat sails due East from a Harbour (H), to a marker buoy (B),15 miles away.
At B the boat turns due South and sails for 6.4 miles to a Lighthouse (L). It then
returns to harbour. What is the total distance travelled by the boat?
15 miles
H
LH
LH
LH
2
15
2
15
2
6.4
B
2
6.4
6.4 miles
2
16.3 miles
Total distance travelled = 21.4 + 16.4 = 37.7 miles
L

24. A 12 ft ladder rests against the side of a house. The top of
the ladder is 9.5 ft from the floor. How far is the base of
the ladder from the house?
L
2
12
L
2
12
L
2
9.5
2
9.5
2
12 ft
9.5 ft
7.3ft
L

25. Finding the shortest distance

28. Ladder to reach the window

29. The amount of area represented by the triangles is
the same for both the left and right sides of the
figure. Take away the triangles.
Then the area of the large square must equal the
area of the two small squares.
This proves the Pythagorean Theorem.