Uploaded byRose Agustina
Trigonometri
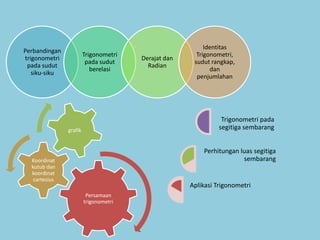
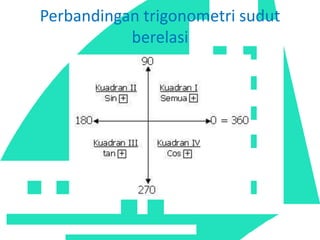
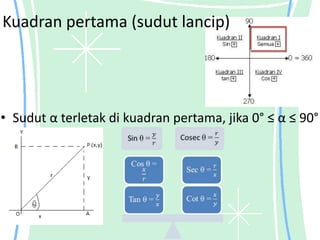
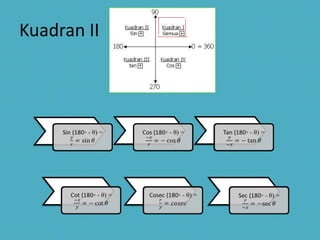
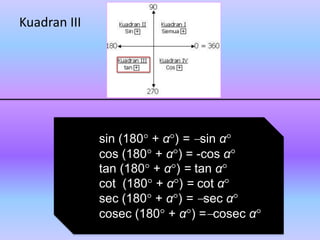
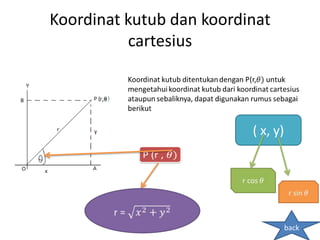
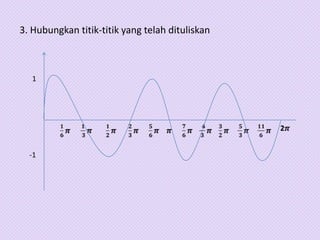
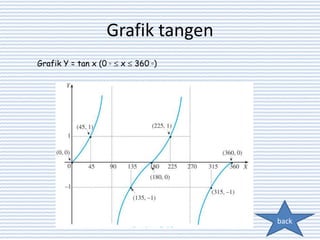
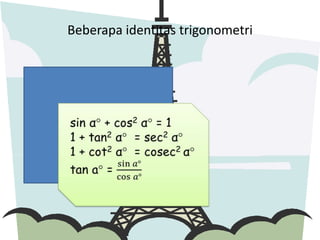
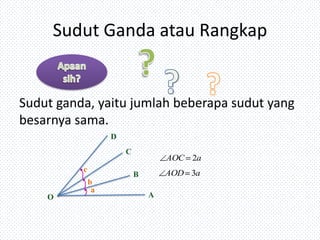
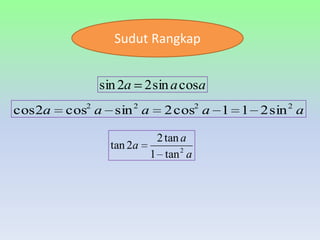
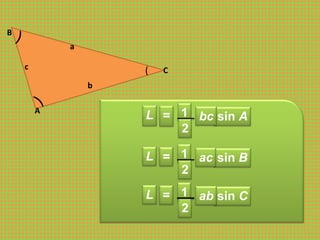
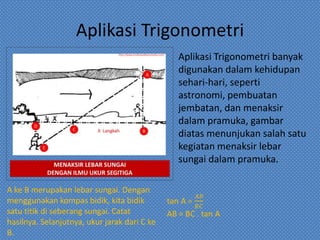
Dokumen tersebut membahas tentang trigonometri, termasuk definisi sudut dalam derajat dan radian, identitas trigonometri, persamaan trigonometri, koordinat kutub dan cartesius, aplikasi trigonometri dalam perhitungan luas segitiga dan gerak benda, serta penggunaan grafik fungsi trigonometri untuk menggambarkan gejala fisika.
More Related Content
Trigonometri
- 1.
- 2. Perbandingan trigonometri pada sudut siku-siku Trigonometri pada sudut berelasi Derajatdan Radian Identitas Trigonometri, sudut rangkap, dan penjumlahan Persamaan trigonometri Koordinat kutub dan koordinat cartesius grafik Aplikasi Trigonometri Perhitungan luas segitiga sembarang Trigonometri pada segitiga sembarang
- 3.
- 4. Radian Satu radian adalahbesar sudut pusat busur lingkaran yang panjangnya sama dengan jari-jari. Π radian = 180 θ = 1 rad r r r
- 5. Contoh soal : Nyatakansudut 72◦ ke satuan radian! r 72 ◦ Radian??? back
- 6. Perbandingan trigonometri padasudut siku-siku miring depan samping θ DEMI DESAh perut SAMI’un MimpinDEmo Minta maSAk SAyur DEngkil MInta maSAk DESAh perut DEMI SAyur DEngkil SAMI’un MimpinDEmo
- 7.
- 8.
- 9. • Sudut αterletak di kuadran pertama, jika 0° ≤ α ≤ 90° Kuadran pertama (sudut lancip)
- 11.
- 12. Kuadran III sin (180+ α ) = sin α cos (180 + α ) = -cos α tan (180 + α ) = tan α cot (180 + α ) = cot α sec (180 + α ) = sec α cosec (180 + α ) = cosec α
- 13.
- 14.
- 15. Sudut lebih dari360◦ atau sudut negatif sin (n 360 + α ) = sin α cos (n 360 + α ) = cos α tan (n 360 + α ) = tan α cot (n 360 + α ) = cot α sec (n 360 + α ) = sec α cosec (n 360 + α ) = cosec α back
- 16. Koordinat kutub dankoordinat cartesius ( x, y) back
- 17. Grafik Trigonometri Langkah-langkah membuatgrafik : 1. Buatlah tabel yang menyatakan hubungan antara x dan y = f (x) . Pilihlah nilai sudut x sehingga nilai y = f(x) dapat dengan mudah ditentukan 2. Titik-titik (x,y) yang diperoleh pada langkah 1 digambar pada bidang cartesius 3. Hubungkan titik-titik pada langkah 2 dengan kurva yang mulus.
- 18. 1. Buat tabeldan pilihlah sudut X 0 3x 0 y= sin 3x 0 1 0 -1 0 1 0 -1 0 1 0 -1 0
- 19. 2. Gambar titik(x,y) yang telah diperoleh 1 -1
- 20. 1 3. Hubungkan titik-titikyang telah dituliskan -1
- 21. Grafik cosinus Grafik y= cos x (0 ◦ x 360 ◦)
- 22. Grafik tangen Grafik Y= tan x (0 ◦ x 360 ◦) back
- 23.
- 24.
- 25. Identitas Trigonometri Suatu bentukkesamaan trigonometri disebut identitas trigonometri apabila berlaku untuk sembarang besar sudut yang diberikan. Identitas trigonometri yang mendasar berguna untuk menghitung nilai dan membuktikan identitas trigonometri lain.
- 26.
- 27. Sudut Ganda atauRangkap Sudut ganda, yaitu jumlah beberapa sudut yang besarnya sama. O D C B A c b a aAOC 2 aAOD 3
- 28. aaa cossin22sin aaaaa 2222 sin211cos2sincos2cos a a a2 tan1 tan2 2tan Sudut Rangkap
- 29. 1) Nyatakan dalamsudut ! Answer: x6sin Contoh soal : x3 xxxx 3cos3sin2)3.(2sin6sin 2) Jika , maka tentukan nilai !! Answer : 5 3 sin A A2cos AA 2 sin212cos 25 7 25 18 25 25 25 9 .21
- 30. Rumus-rumus penjumlahan dan selisihsudut ba ba ba tantan1 tantan )tan( ba ba ba tantan1 tantan )tan( cos (a+b) = cos a cos b – sin a sin b cos (a-b) = cos a cos b + sin a sin b sin (a+b) = sin a cos b + cos a sin b sin (a-b) = sin a cos b - cos a sin b
- 31. Contoh soal :Diketahui dan . Jika sudut A dan B lancip,tentukan nilai cos (A-B)! 5 4 cosA 5 3 cosB BaBABA sinsincoscos)cos( 5 4 . 5 3 5 3 . 5 4 25 24 back
- 32. Trigonometri pada segitigasembarang 1. Aturan sinus Aturan sinus dapat digunakan dengan memenuhi salah satu dari ketiga syarat : a. Dua sisi dan satu sudut dihadapanya diketahui b. Dua sudut dan satu sisi dihadapannya diketahui c. Dua sudut dan dua sisi diketahui
- 33. a2 = b2+ c2 2bc cos A b2 = a2 + c2 2ac cos B c2 = a2 + b2 2ac cos C 2. Aturan cosinus Aturan cosinus dapat digunakan dengan memenuhi salah satu dari syarat : a. Tiga sisi diketahui b. Dua sisi diketahui satu sudut diketahui
- 34. Aplikasi trigonometri dalam perhitunganluas segitiga sembarang
- 35. sin AbcL =1 2 sin BacL = 1 2 sin CabL = 1 2 B C A b a c (
- 36. Menghitung luas segitigasembarang dengan tiga sisi diketahui s = ½ (a + b + c) = setengah keliling ABC. back
- 37. Aplikasi Trigonometri Aplikasi Trigonometribanyak digunakan dalam kehidupan sehari-hari, seperti astronomi, pembuatan jembatan, dan menaksir dalam pramuka, gambar diatas menunjukan salah satu kegiatan menaksir lebar sungai dalam pramuka. A ke B merupakan lebar sungai. Dengan menggunakan kompas bidik, kita bidik satu titik di seberang sungai. Catat hasilnya. Selanjutnya, ukur jarak dari C ke B.
- 38. Pemakaian grafik fungsitrigonometri Banyak gejala fisika,teknik dan lain sebagainya dapat dinyatakan sebagai fungsi trigonometri. Salah satu diantaranya adalah gerak berayun, dan gerak planet mengelilingi matahari . 0, -A -A , 0 A , 0 0, A Y X Sekarang, misalkan kita memperhatikan gerak bumi mengelilingi matahari. Kita asumsikan bahwa gerak bumi tersebut berbentuk lingkaran dengan pusat di matahari. Pada sistem ini di asumsikan ada sumbu kordinat. Kemudian gerak dari bumi tersebut di proyeksikan ke sumbu vertikal Y. jika bumi berputar pada lingkaran ,benda proyeksi akan berayun sepanjang sumbu Y . Misalkan pada awalnya bumi sumbu X positif, maka benda proyeksi akan berada di pusat (0,0). back