Pemetaan kelas x
•Download as DOCX, PDF•
1 like•1,082 views
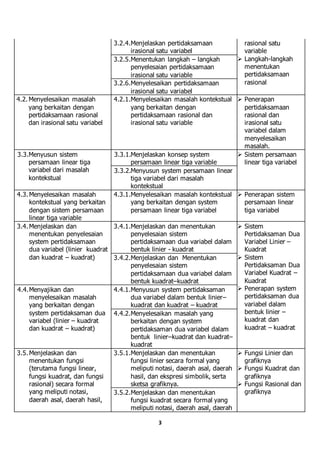
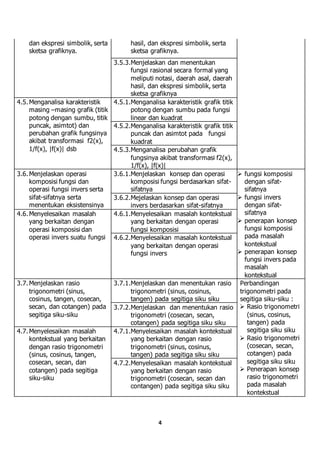
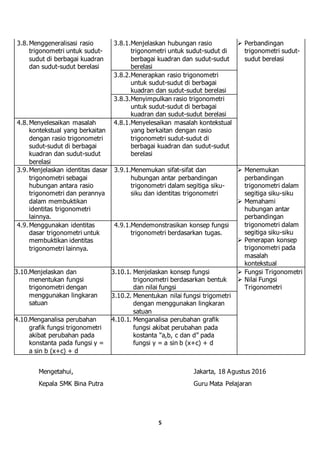
Dokumen tersebut merupakan pemetaan mata pelajaran matematika untuk tahun pelajaran 2016/2017 di SMK Bina Putra. Dokumen tersebut memuat kompetensi dasar, indikator pencapaian, materi pembelajaran, dan prestasi yang akan dicapai siswa untuk setiap kompetensi dasar. Dokumen ini disusun oleh guru matematika Faqih Makhfuddin, S.Pd untuk memandu proses pembelajaran matematika di kelas X semester 1
More Related Content
What's hot
What's hot (20)
Viewers also liked
Viewers also liked (20)
Similar to Pemetaan kelas x
Similar to Pemetaan kelas x (14)
Recently uploaded
Recently uploaded (20)
Pemetaan kelas x
- 1. 1 PEMETAAN M A T E M A T I K A Kelas/Semester : X / 1-2 Nama Guru : Faqih Makhfuddin, S. Pd Sekolah Menengah Kejuruan Bina Putra Jakarta
- 2. 2 2016-2017 PEMETAAN TAHUN PELAJARAN 2016/2017 Nama Sekolah : SMK BINA PUTRA Kelas/Semester : X/1 dan 2 Mata Pelajaran : Matematika KOMPETENSI DASAR INDIKATOR PENCAPAIAN PRESTASI MATERI PEMBELAJARAN 3.1.Mengintepretasi persamaan dan pertidaksamaan nilai mutlak dari bentuk linear satu variabel dengan persamaan dan pertidaksamaan linear Aljabar lainnya 3.1.1.Menjelaskan pengertian persamaan nilai mutlak dari bentuk linear satu variabel Pengertian persamaan dan pertidaksamaan nilai mutlak dari bentuk linear satu variabel. 3.1.2.Menjelaskan pengertian pertidaksamaan nilai mutlak dari bentuk linear satu variabel 3.1.3.Menyelesaikan pengertian persamaan nilai mutlak dari bentuk linear satu variabel Menyelesaikan persamaan dan pertidaksamaan nilai mutlak dari bentuk linear satu variabel 3.1.4.Menyelesaikan pengertian pertidaksamaan nilai mutlak dari bentuk linear satu variabel 4.1.Menyelesaikan masalah yang berkaitan dengan persamaan dan pertidaksamaan nilai mutlak dari bentuk linear satu variable 4.1.1.Menyelesaikan masalah yang berkaitan dengan persamaan nilai mutlak dari bentuk variable Penerapan nilai mutlak dalam menyelesaikan masalah yang berkaitan dengan persamaan dan pertidaksamaan nilai mutlak dari bentuk linear satu variabel 4.1.2.Menyelesaikan masalah yang berkaitan dengan pertidaksamaan nilai mutlak dari bentuk variable 3.2.Menjelaskan dan menentukan penyelesaian pertidaksamaan rasional dan irasional satu variable 3.2.1.Menjelaskan pertidaksamaan rasional satu variable Pengertian pertidaksamaan rasional satu variable Syarat-syarat pertidaksamaan 3.2.2.Menentukan langkah – langkah penyelesaian pertidaksamaan rasional satu variable 3.2.3.Menyelesaikan pertidaksamaan rasional satu variabel
- 3. 3 3.2.4.Menjelaskan pertidaksamaan irasional satu variabel rasional satu variable Langkah-langkah menentukan pertidaksamaan rasional 3.2.5.Menentukan langkah – langkah penyelesaian pertidaksamaan irasional satu variable 3.2.6.Menyelesaikan pertidaksamaan irasional satu variabel 4.2.Menyelesaikan masalah yang berkaitan dengan pertidaksamaan rasional dan irasional satu variabel 4.2.1.Menyelesaikan masalah kontekstual yang berkaitan dengan pertidaksamaan rasional dan irasional satu variable Penerapan pertidaksamaan rasional dan irasional satu variabel dalam menyelesaikan masalah. 3.3.Menyusun sistem persamaan linear tiga variabel dari masalah kontekstual 3.3.1.Menjelaskan konsep system persamaan linear tiga variable Sistem persamaan linear tiga variabel 3.3.2.Menyusun system persamaan linear tiga variabel dari masalah kontekstual 4.3.Menyelesaikan masalah kontekstual yang berkaitan dengan sistem persamaan linear tiga variable 4.3.1.Menyelesaikan masalah kontekstual yang berkaitan dengan system persamaan linear tiga variabel Penerapan sistem persamaan linear tiga variabel 3.4.Menjelaskan dan menentukan penyelesaian system pertidaksamaan dua variabel (linier kuadrat dan kuadrat – kuadrat) 3.4.1.Menjelaskan dan menentukan penyelesaian sistem pertidaksamaan dua variabel dalam bentuk linier - kuadrat Sistem Pertidaksaman Dua Variabel Linier – Kuadrat Sistem Pertidaksaman Dua Variabel Kuadrat – Kuadrat Penerapan system pertidaksaman dua variabel dalam bentuk linier – kuadrat dan kuadrat – kuadrat 3.4.2.Menjelaskan dan Menentukan penyelesaian sistem pertidaksamaan dua variabel dalam bentuk kuadrat–kuadrat 4.4.Menyajikan dan menyelesaikan masalah yang berkaitan dengan system pertidaksaman dua variabel (linier – kuadrat dan kuadrat – kuadrat) 4.4.1.Menyusun system pertidaksaman dua variabel dalam bentuk linier– kuadrat dan kuadrat – kuadrat 4.4.2.Menyelesaikan masalah yang berkaitan dengan system pertidaksaman dua variabel dalam bentuk linier–kuadrat dan kuadrat– kuadrat 3.5.Menjelaskan dan menentukan fungsi (terutama fungsi linear, fungsi kuadrat, dan fungsi rasional) secara formal yang meliputi notasi, daerah asal, daerah hasil, 3.5.1.Menjelaskan dan menentukan fungsi linier secara formal yang meliputi notasi, daerah asal, daerah hasil, dan ekspresi simbolik, serta sketsa grafiknya. Fungsi Linier dan grafiknya Fungsi Kuadrat dan grafiknya Fungsi Rasional dan grafiknya3.5.2.Menjelaskan dan menentukan fungsi kuadrat secara formal yang meliputi notasi, daerah asal, daerah
- 4. 4 dan ekspresi simbolik, serta sketsa grafiknya. hasil, dan ekspresi simbolik, serta sketsa grafiknya. 3.5.3.Menjelaskan dan menentukan fungsi rasional secara formal yang meliputi notasi, daerah asal, daerah hasil, dan ekspresi simbolik, serta sketsa grafiknya 4.5.Menganalisa karakteristik masing –masing grafik (titik potong dengan sumbu, titik puncak, asimtot) dan perubahan grafik fungsinya akibat transformasi f2(x), 1/f(x), |f(x)| dsb 4.5.1.Menganalisa karakteristik grafik titik potong dengan sumbu pada fungsi linear dan kuadrat 4.5.2.Menganalisa karakteristik grafik titik puncak dan asimtot pada fungsi kuadrat 4.5.3.Menganalisa perubahan grafik fungsinya akibat transformasi f2(x), 1/f(x), |f(x)| 3.6.Menjelaskan operasi komposisi fungsi dan operasi fungsi invers serta sifat-sifatnya serta menentukan eksistensinya 3.6.1.Menjelaskan konsep dan operasi komposisi fungsi berdasarkan sifat- sifatnya fungsi komposisi dengan sifat- sifatnya fungsi invers dengan sifat- sifatnya penerapan konsep fungsi komposisi pada masalah kontekstual penerapan konsep fungsi invers pada masalah kontekstual 3.6.2.Mejelaskan konsep dan operasi invers berdasarkan sifat-sifatnya 4.6.Menyelesaikan masalah yang berkaitan dengan operasi komposisi dan operasi invers suatu fungsi 4.6.1.Menyelesaikan masalah kontekstual yang berkaitan dengan operasi fungsi komposisi 4.6.2.Menyelesaikan masalah kontekstual yang berkaitan dengan operasi fungsi invers 3.7.Menjelaskan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku 3.7.1.Menjelaskan dan menentukan rasio trigonometri (sinus, cosinus, tangen) pada segitiga siku siku Perbandingan trigonometri pada segitiga siku-siku : Rasio trigonometri (sinus, cosinus, tangen) pada segitiga siku siku Rasio trigonometri (cosecan, secan, cotangen) pada segitiga siku siku Penerapan konsep rasio trigonometri pada masalah kontekstual 3.7.2.Menjelaskan dan menentukan rasio trigonometri (cosecan, secan, cotangen) pada segitiga siku siku 4.7.Menyelesaikan masalah kontekstual yang berkaitan dengan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku 4.7.1.Menyelesaikan masalah kontekstual yang berkaitan dengan rasio trigonometri (sinus, cosinus, tangen) pada segitiga siku siku 4.7.2.Menyelesaikan masalah kontekstual yang berkaitan dengan rasio trigonometri (cosecan, secan dan contangen) pada segitiga siku siku
- 5. 5 3.8.Menggeneralisasi rasio trigonometri untuk sudut- sudut di berbagai kuadran dan sudut-sudut berelasi 3.8.1.Menjelaskan hubungan rasio trigonometri untuk sudut-sudut di berbagai kuadran dan sudut-sudut berelasi Perbandingan trigonometri sudut- sudut berelasi 3.8.2.Menerapkan rasio trigonometri untuk sudut-sudut di berbagai kuadran dan sudut-sudut berelasi 3.8.3.Menyimpulkan rasio trigonometri untuk sudut-sudut di berbagai kuadran dan sudut-sudut berelasi 4.8.Menyelesaikan masalah kontekstual yang berkaitan dengan rasio trigonometri sudut-sudut di berbagai kuadran dan sudut-sudut berelasi 4.8.1.Menyelesaikan masalah kontekstual yang berkaitan dengan rasio trigonometri sudut-sudut di berbagai kuadran dan sudut-sudut berelasi 3.9.Menjelaskan identitas dasar trigonometri sebagai hubungan antara rasio trigonometri dan perannya dalam membuktikan identitas trigonometri lainnya. 3.9.1.Menemukan sifat-sifat dan hubungan antar perbandingan trigonometri dalam segitiga siku- siku dan identitas trigonometri Menemukan perbandingan trigonometri dalam segitiga siku-siku Memahami hubungan antar perbandingan trigonometri dalam segitiga siku-siku Penerapan konsep trigonometri pada masalah kontekstual 4.9.Menggunakan identitas dasar trigonometri untuk membuktikan identitas trigonometri lainnya. 4.9.1.Mendemonstrasikan konsep fungsi trigonometri berdasarkan tugas. 3.10.Menjelaskan dan menentukan fungsi trigonometri dengan menggunakan lingkaran satuan 3.10.1. Menjelaskan konsep fungsi trigonometri berdasarkan bentuk dan nilai fungsi Fungsi Trigonometri Nilai Fungsi Trigonometri 3.10.2. Menentukan nilai fungsi trigometri dengan menggunakan lingkaran satuan 4.10.Menganalisa perubahan grafik fungsi trigonometri akibat perubahan pada konstanta pada fungsi y = a sin b (x+c) + d 4.10.1. Menganalisa perubahan grafik fungsi akibat perubahan pada kostanta “a,b, c dan d” pada fungsi y = a sin b (x+c) + d Mengetahui, Jakarta, 18 Agustus 2016 Kepala SMK Bina Putra Guru Mata Pelajaran
- 6. 6 H. Muhammad, S. Pd Faqih Makhfuddin, S. Pd