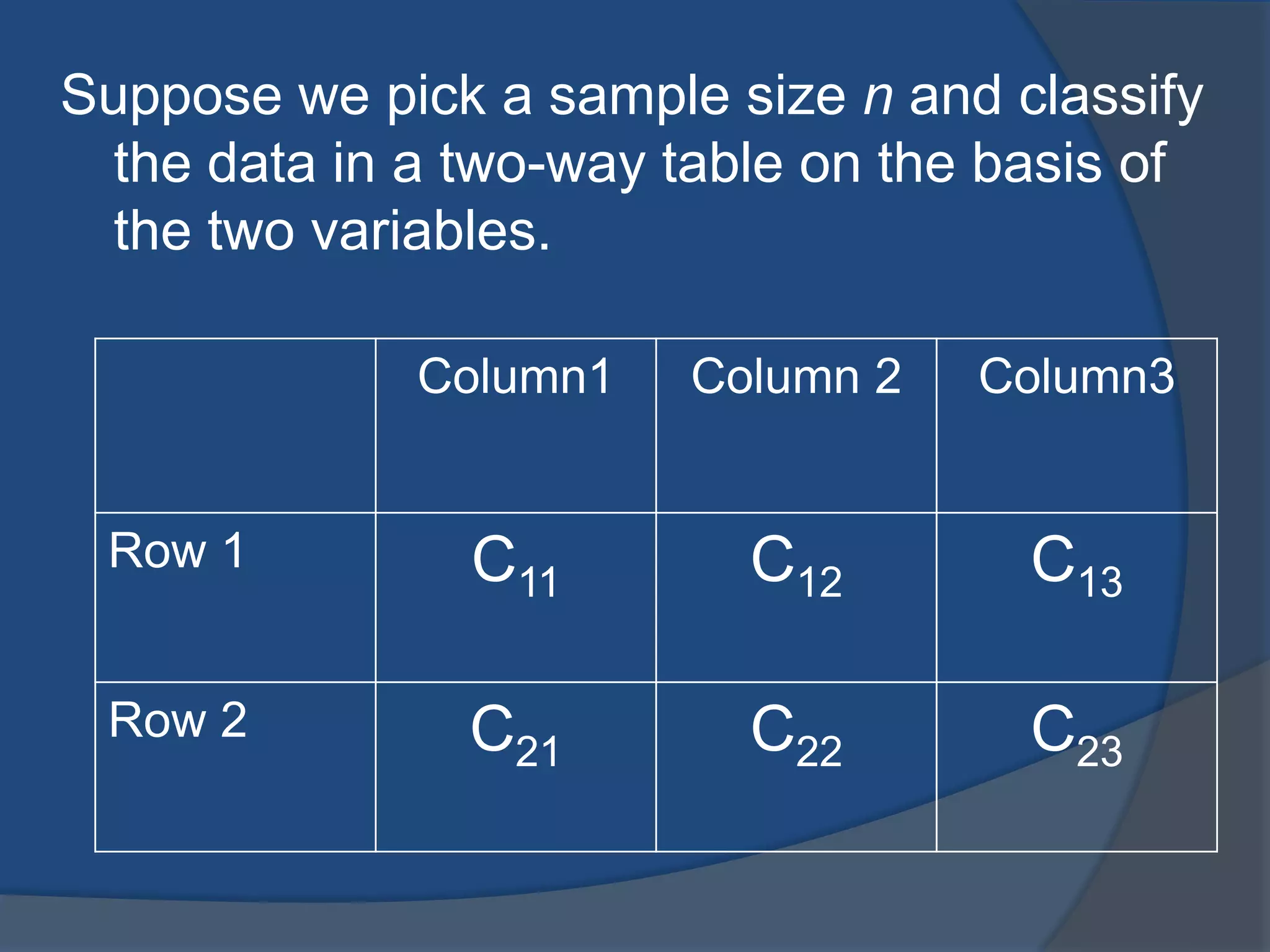
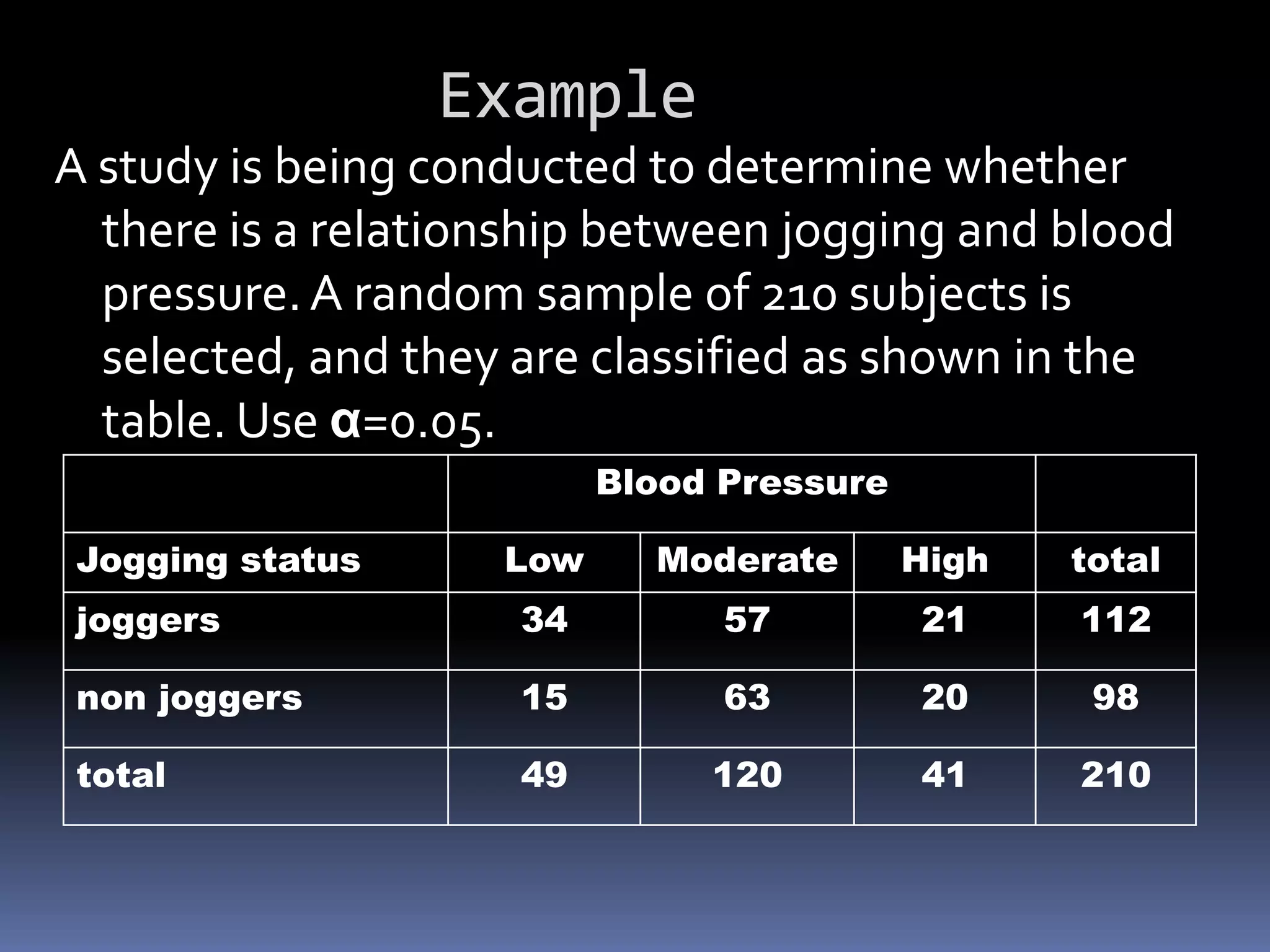
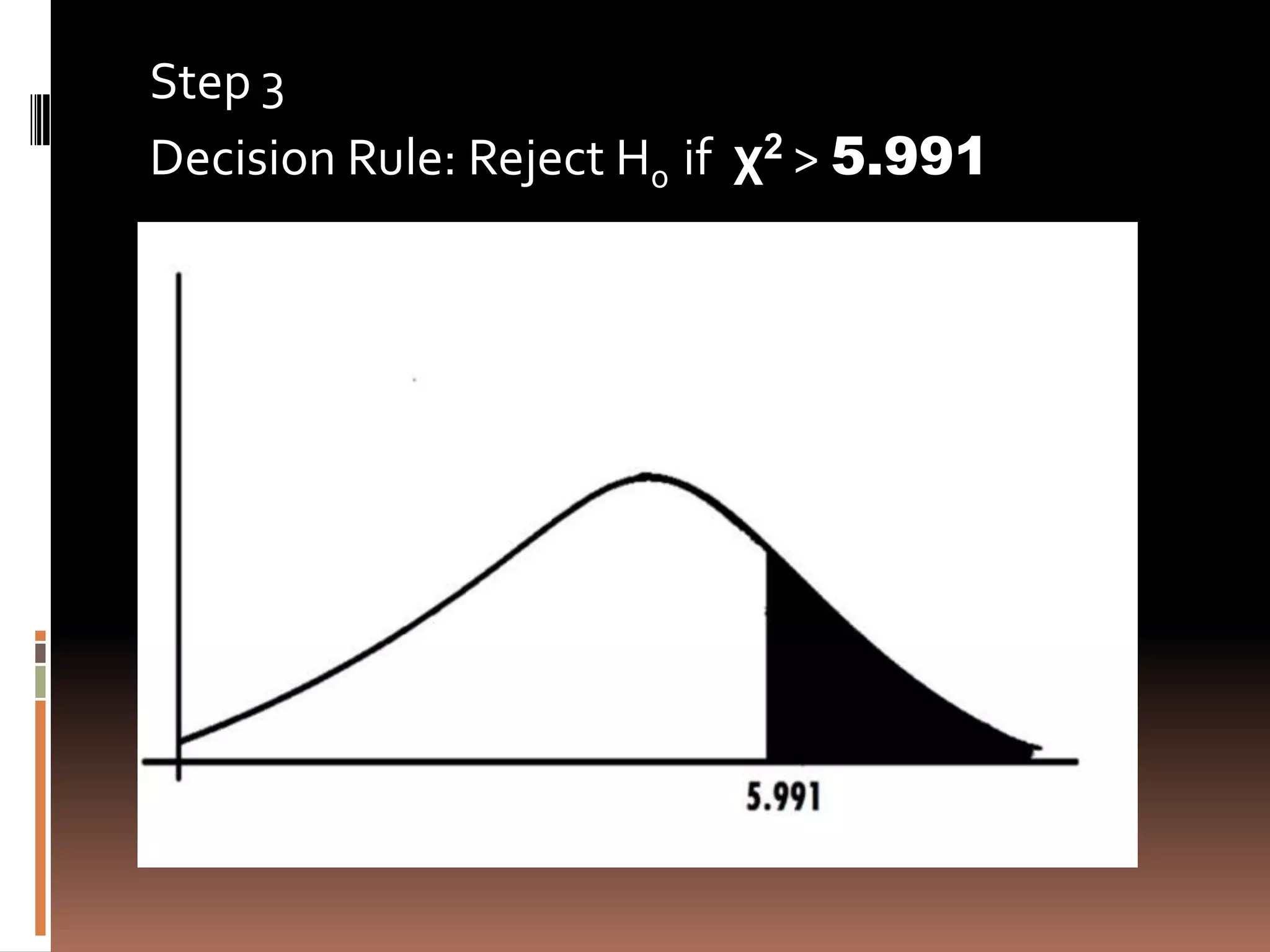
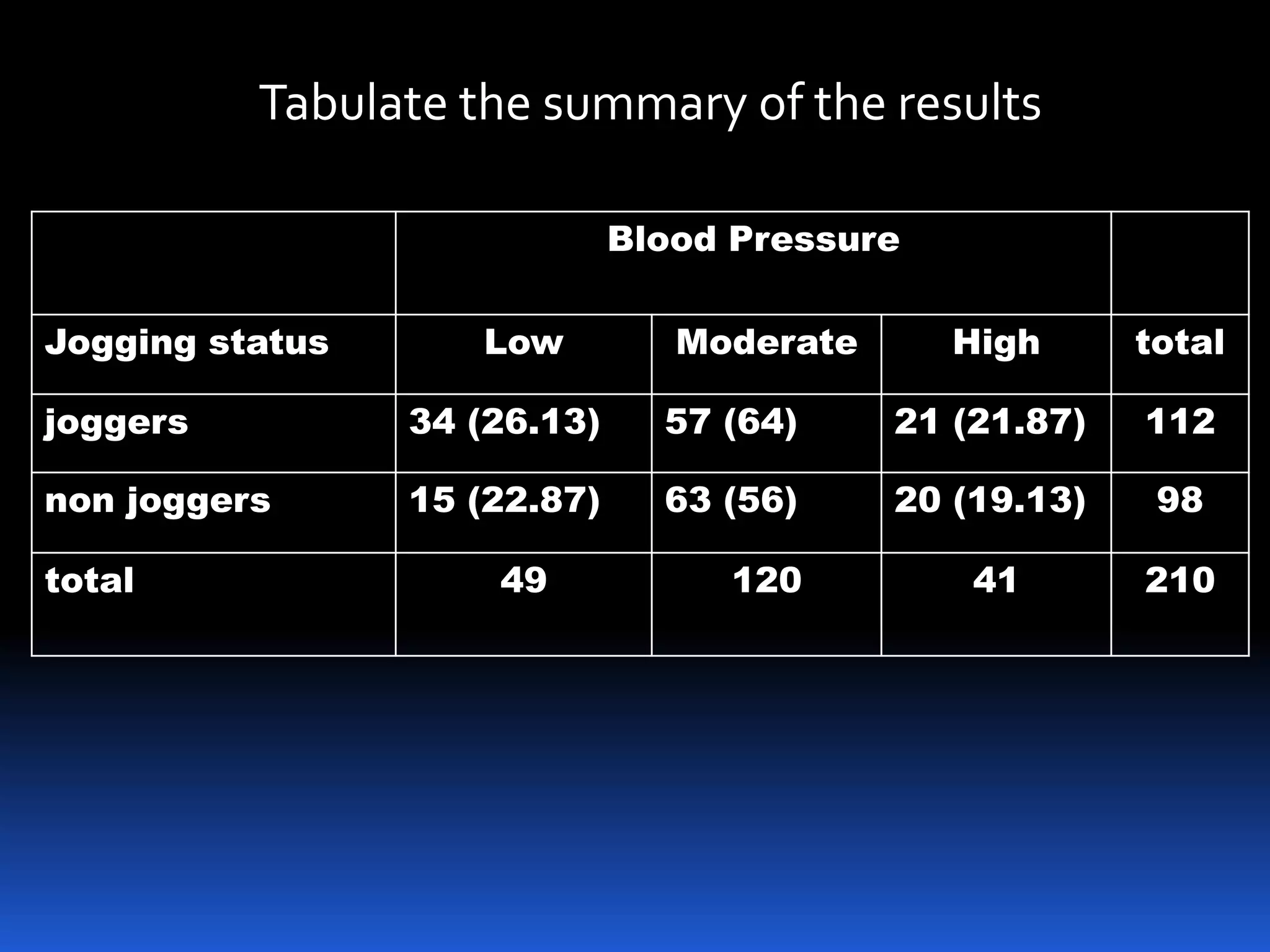
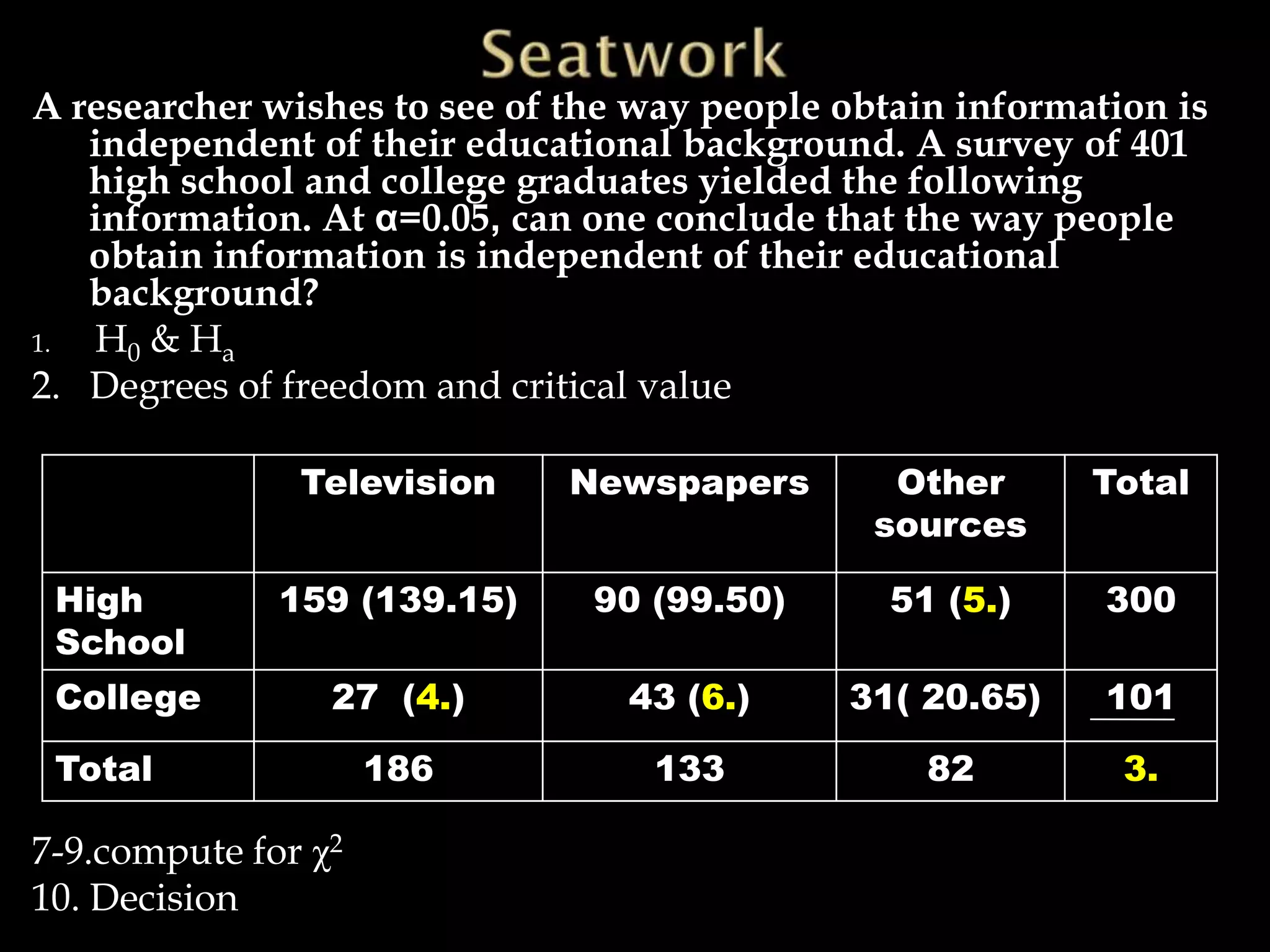
The document discusses testing for independence between two variables using a contingency table and chi-square test. It explains how to set up a contingency table with observed and expected frequencies, and how to calculate the chi-square test statistic to determine if the variables are independent or dependent. An example is provided that tests if blood pressure is independent of jogging status using a contingency table and chi-square test.

1. Test
for Independence

2. Test of Independence
The goal is to find whether two observed
characteristics of a member of a population
are independent.
Contingency Table
-a table for determining whether the distribution
according to one variable is contingent on the
distribution of the other.
-is made up of R rows and C columns.
-is designated as R x C table

3. Suppose we pick a sample size n and classify
the data in a two-way table on the basis of
the two variables.
Column1 Column 2 Column3
Row 1 C11 C12 C13
Row 2 C21 C22 C23

5. The degrees of freedom for any contingency
table are
(no. of rows-1) x (no. of columns-1) or
v= (R-1) (C-1)
If x2>xa2 with v=(r-1)(c-1) degrees of
freedom, reject the null hypothesis of
independence at the a level of
significance; otherwise, accept the null
hypothesis.

6. Computation of Expected
Frequencies
1. Find the sum of each row and each
column, and find the grand total.
2. For each cell, multiply the
corresponding row sum by the column
sum and divide by the grand total, to
get the expected value.
3. Place the expected values in the
corresponding cells along with the
observed values.

7. The general formula for obtaining the expected
frequency of any cell is given by:
Expected frequency=(column total)x (row total)
grand total

8. Example
A study is being conducted to determine whether
there is a relationship between jogging and blood
pressure. A random sample of 210 subjects is
selected, and they are classified as shown in the
table. Use α=0.05.
Blood Pressure
Jogging status Low Moderate High total
joggers 34 57 21 112
non joggers 15 63 20 98
total 49 120 41 210

9. Solution
Step 1
H0: The blood pressure of a person does not depend
on whether he jogs or not.
Ha: The blood pressure of a person depends on
whether he jogs or not.
Step 2
Determine the critical value.
v= (R-1) (C-1)
= (2-1) (3-1)
= (1) (2)
v= 2
Using the table, the critical value is 5.991.

10. Step 3
Decision Rule: Reject H0 if χ2 > 5.991

11. Step 4
Compute the test statistic. First, compute for the
expected values
E11=(112)(49) = 26.13 E22=(98) (120) = 56
210 210
E21=(98)(49) E13=(112) (41)
= 22.87 = 21.87
210 210
E12=(112)(120) E23=(98) (41)
= 64 = 19.13
210 210

12. The expected frequency for each cell is
recorded in parentheses beside the
actual observed value. Note that the
expected frequencies in any row or
column add up to the appropriate
marginal total. In our example we may
compute only the three expected
frequencies in the top row of the table
and then find the others by subtraction.

13. Tabulate the summary of the results
Blood Pressure
Jogging status Low Moderate High total
joggers 34 (26.13) 57 (64) 21 (21.87) 112
non joggers 15 (22.87) 63 (56) 20 (19.13) 98
total 49 120 41 210

14. The chi-square value is
Χ2 = Σ (oi - ei)2
i
ei
χ2= (34-26.13)2 + (15-22.87)2 + (57-64)2
26.13 22.87 64
+ (63-56)2 + (21-21.87)2 + (20-19.13)2
56 21.87 125.8
=6.79

15. Step 5
Make the decision
Since 6.79 > 5.991, reject H0. Hence, the blood
pressure of a person depends on whether he
jogs or not.

17. A researcher wishes to see of the way people obtain information is
independent of their educational background. A survey of 401
high school and college graduates yielded the following
information. At α=0.05, can one conclude that the way people
obtain information is independent of their educational
background?
1. H0 & Ha
2. Degrees of freedom and critical value
Television Newspapers Other Total
sources
High 159 (139.15) 90 (99.50) 51 (5.) 300
School
College 27 (4.) 43 (6.) 31( 20.65) 101
Total 186 133 82 3.
7-9.compute for χ2
10. Decision

18. 1. H0: The way people obtain information is
independent of their educational background.
Ha: The way people obtain information is
dependent of their educational background.
2. n=2, a=5.991 10. since χ2 > χa2,
3. 401 reject H0
4. 46.85
5. 61.35
6. 33.50
7-9. χ2= 46.19

19. Voting Preferences
Republican Democrat Independent Row Total
Male 200 150 50 400
Female 250 300 50 600
Column 450 450 100 1000
total
Do the men's voting preferences differ significantly from the
women's preferences? Use a 0.05 level of significance.