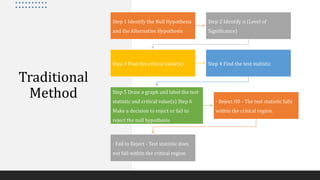
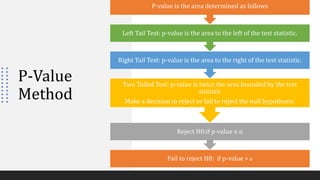
The document describes two common methods for hypothesis testing: 1) The traditional method involves identifying the null and alternative hypotheses, significance level, critical values, test statistic, and making a decision to reject or fail to reject the null hypothesis. 2) The p-value method compares the p-value to the significance level (α) to decide whether to reject or fail to reject the null hypothesis. All hypothesis tests follow the same general steps: state hypotheses, formulate an analysis plan, analyze sample data, and interpret results to accept or reject the null hypothesis.

1. Methods of
Hypothesis Testing
Dr. Kshitija Gandhi
PHD, MPHIL, MCOM,MBA,UGC NET
Vice Principal
Pratibha College of
Commerce and Computer studies

2. Traditional
Method
Step 1 Identify the Null Hypothesis
and the Alternative Hypothesis
Step 2 Identify α (Level of
Significance)
Step 3 Find the critical value(s) Step 4 Find the test statistic
Step 5 Draw a graph and label the test
statistic and critical value(s) Step 6
Make a decision to reject or fail to
reject the null hypothesis
· Reject H0 - The test statistic falls
within the critical region.
· Fail to Reject - Test statistic does
not fall within the critical region.

3. P-Value
Method
Fail to reject H0: if p-value > α
Reject H0:if p-value ≤ α
Two Tailed Test: p-value is twice the area bounded by the test
statistic
Make a decision to reject or fail to reject the null hypothesis:
Right Tail Test: p-value is the area to the right of the test statistic.
Left Tail Test: p-value is the area to the left of the test statistic.
P-value is the area determined as follows

4. Conclusion
All hypothesis tests
are conducted the
same way.
The researcher states
a hypothesis to be
tested, formulates an
analysis plan
Analyzes sample data
according to the plan,
Accepts or rejects the
null hypothesis,
based on results of
the analysis.

5. State the
Hypotheses
Every hypothesis test requires the
analyst to state a null
hypothesis and an alternative
hypothesis.
The hypotheses are stated in such a
way that they are mutually
exclusive.
That is, if one is true, the other
must be false; and vice versa.

6. Formulate an
Analysis Plan
The analysis plan describes how to use sample
data to accept or reject the null hypothesis.
It should specify the following elements.
Significance level.
Often, researchers choose significance levels equal
to 0.01, 0.05, or 0.10; but any value between 0 and
1 can be used.

7. Formulate an Analysis Plan
• Test method. Typically, the test method involves a test statistic
and a sampling distribution.
• Computed from sample data, the test statistic might be a mean
score, proportion, difference between means, difference
between proportions, z-score, t statistic, chi-square, etc.
• Given a test statistic and its sampling distribution, a researcher
can assess probabilities associated with the test statistic. If the
test statistic probability is less than the significance level, the
null hypothesis is rejected.

8. Analyze sample data.
Using sample data, perform computations called for in the analysis plan.
Test statistic. When the null hypothesis involves a mean or proportion, use either of the following
equations to compute the test statistic.
Test statistic = (Statistic - Parameter) / (Standard deviation of statistic)
Test statistic = (Statistic - Parameter) / (Standard error of statistic)
• where Parameter is the value appearing in the null hypothesis,
• Statistic is the point estimate of Parameter.
• As part of the analysis, you may need to compute the standard deviation or standard error of the
statistic. Previously, we presented common formulas for the standard deviation and standard error.
When the parameter in the null hypothesis involves categorical data, you may use a chi-square statistic
as the test statistic. Instructions for computing a chi-square test statistic are presented in the lesson on
the chi-square goodness of fit test.
• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic,
assuming the null hypothesis is true.

9. Analyze
sample data.
• When the parameter in the null hypothesis involves
categorical data, use a chi-square statistic as the test
statistic. Instructions for computing a chi-square test
statistic are presented in the lesson on the chi-
square goodness of fit test.
• P-value. The P-value is the probability of observing a
sample statistic as extreme as the test statistic,
assuming the null hypothesis is true.

10. Interpret
the Results
If the sample findings are unlikely, given the
null hypothesis, the researcher rejects the null
hypothesis. Typically, this involves comparing
the P-value to the significance level, and
rejecting the null hypothesis when the P-value
is less than the significance level.

11. Problem 1: Two-Tailed Test
• The CEO of a large electric utility claims that 80 percent of his
1,000,000 customers are very satisfied with the service they
receive. To test this claim, the local newspaper surveyed 100
customers, using simple random sampling. Among the sampled
customers, 73 percent say they are very satisfied.
• Based on these findings, can we reject the CEO's hypothesis that
80% of the customers are very satisfied?
• Use a 0.05 level of significance.

12. Solution
The solution to this problem takes four
steps:
 State the hypotheses
 Formulate an analysis plan
 Analyze sample data
 Interpret results

13. State the Hypotheses
• The first step is to state the null hypothesis and an alternative
hypothesis.
• Null hypothesis: P = 0.80
• Alternative hypothesis: P ≠ 0.80
• Note that these hypotheses constitute a two-tailed test. The null
hypothesis will be rejected if the sample proportion is too big or if it is
too small.

14. Formulate an Analysis
Plan
For this analysis, the significance level is
0.05. The test method, shown in the
next section, is a one-sample z-test.

15. Analyze sample data.
• Using sample data, we calculate the standard
deviation (σ) and compute the z-score test
statistic
• (z).σ = sqrt[ P * ( 1 - P ) / n ]
• σ = sqrt [(0.8 * 0.2) / 100]
• σ = sqrt(0.0016) = 0.04
• z = (p - P) / σ = (.73 - .80)/0.04 = -1.75
• where P is the hypothesized value of population
proportion in the null hypothesis, p is the sample
proportion, and n is the sample size.

16. Analyze
sample
data.
• Since we have a two-tailed test,
the P-value is the probability
that the z-score is less than -1.75
or greater than 1.75.
• We use the Normal Distribution
Calculator to find P(z < -1.75) =
0.04, and P(z > 1.75) = 0.04.
Thus, the P-value = 0.04 + 0.04 =
0.08.

17. Interpret
Results
• Since the P-value (0.08) is
greater than the significance
level (0.05), we cannot reject the
null hypothesis.