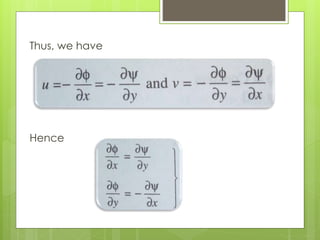
1. The document discusses the differences between the velocity potential function (f) and the stream function (y) for fluid flow. 2. The velocity potential function applies to irrotational flows and satisfies the Laplace equation, while the stream function can apply to both rotational and irrotational flows. 3. A key relationship is that equipotential lines defined by f=constant are perpendicular to streamlines defined by y=constant.

1. Shantilal Shah
Engineering College
Production
Engineering
Sem.- 4 th.
Group- 22

2. Velocity Potential & Potential Flow,
Relation between Stream function &
Velocity Potential
by: Pratik Vadher 130430125113
Guided by :
Prof. Vinay A Parikh
Prof. Prashant V Sartanpara
Prof. Nital P Nirmal

3. DIFFERENCES BETWEEN f and y
1. Flow field variables are found by:
 Differentiating f in the same direction as velocities
 Differentiating y in direction normal to velocities
2. Potential function f applies for irrotational flow only
3. Stream function y applies for rotational or irrotational flows
4. Potential function f applies for 2D flows [f(x,y) or f(r,q)] and 3D flows
[f(x,y,z) or f(r,q, f)]
5. Stream function y applies for 2D y(x,y) or y(r, q) flows only
6. Stream lines (y =constant) and equipotential lines (f =constant) are
mutually perpendicular
 Slope of a line with y =constant is the negative reciprocal of the
slope of a line with f =constant

4. Velocity Potential Function
It is defined as a scalar function of space & time such
that its negative derivative w.r.t any direction gives the
fluid velocity in that direction. It is defined by f (Phi).
Mathematically, the velocity, potential is defined as
f = f (x,y,z) for steady flow such that

5. Where u, v and w are the components of velocity in x, y &
z directions respectively.
The velocity components in cylindrical polar co-ordinates
in terms of velocity potential function are given by
Where Ur = Velocity component in radial direction
& Uq = Velocity component in tangential direction

6. The continuity equation for an incompressible steady
flow is
Substituting the values of u, v & w from above
equation, we get

7. For two-dimensional case, above equation reduces
to
If any value of f (Phi) that satisfies the Laplace
equation, will correspond to some case of fluid flow.
Properties of the Potential function. The rotational
components are given by
Conti..

8. Substituting the values of u, v and w from equation in
the above rotational components, we get

9. If f is a continuous function,
Then equ.
Therefore
When rotational components are zero, the flow is called
irrotational. Hence the properties of the potential function are :
1. If velocity potential (f) exits, the flow should be irrotational.
2. If velocity potential (f) satisfies the Laplace equ. It represents
the possible steady incompressible irrotational flow.

10. Stream Function
It is defined as the scalar function of space & time,
such that it’s partial derivative w.r.t any direction
gives the velocity component at right angles to that
direction. It is denoted as y (Psi) and defined only
for two-dimensional flow. Mathematically, for
steady flow it is defined as y = f(x,y) such that
And

11. The velocity components in cylindrical polar
co-ordinates in terms of stream function are given
as
Where Ur = radial velocity and Uq= tangential
velocity.
The continuity equation for two dimensional
flow is

12. Substituting the values of u and v from above
equation, we get
Hence existence of y means a possible case of fluid
flow. The flow may be rotational or irrotational.
The rotational component Wz is
Given by

13. Substituting the values of u and v from equation in
the above rotational component, we get
For irrotational flow, Wz = 0. Hence above equation
becomes as
Which is Laplace equation for y.

14. The Properties of Stream Function (y) are :
1. If stream function (y) exists, it is possible case of
fluid flow which may be rotational or irrotational.
2. If stream function (y) satisfies the Laplace
equation, it is a possible case of an irrotational
flow.

15. Relation between Stream Function &
Velocity Potential Functions
We have,
From stream function equation we have,

16. Thus, we have
Hence