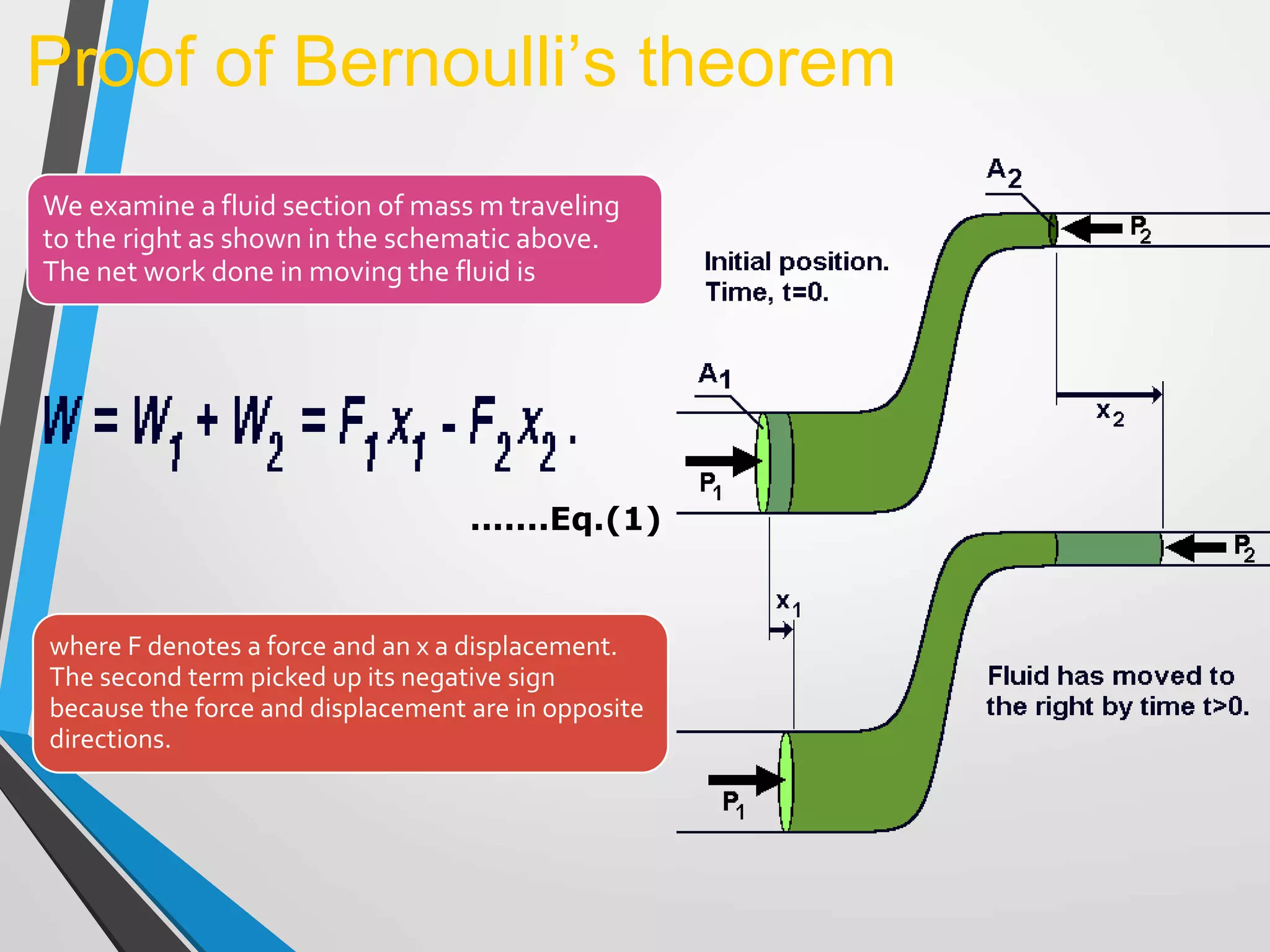
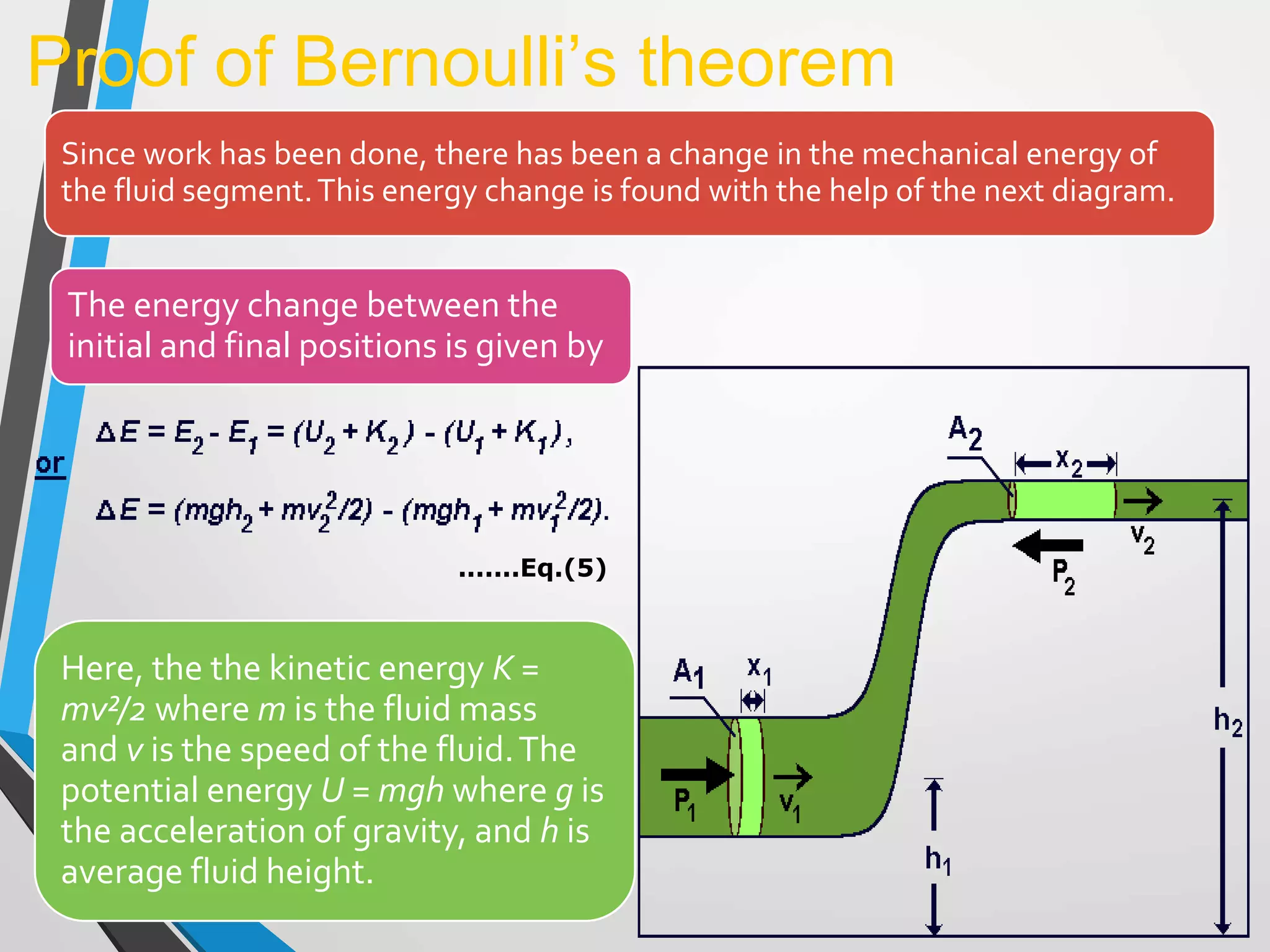
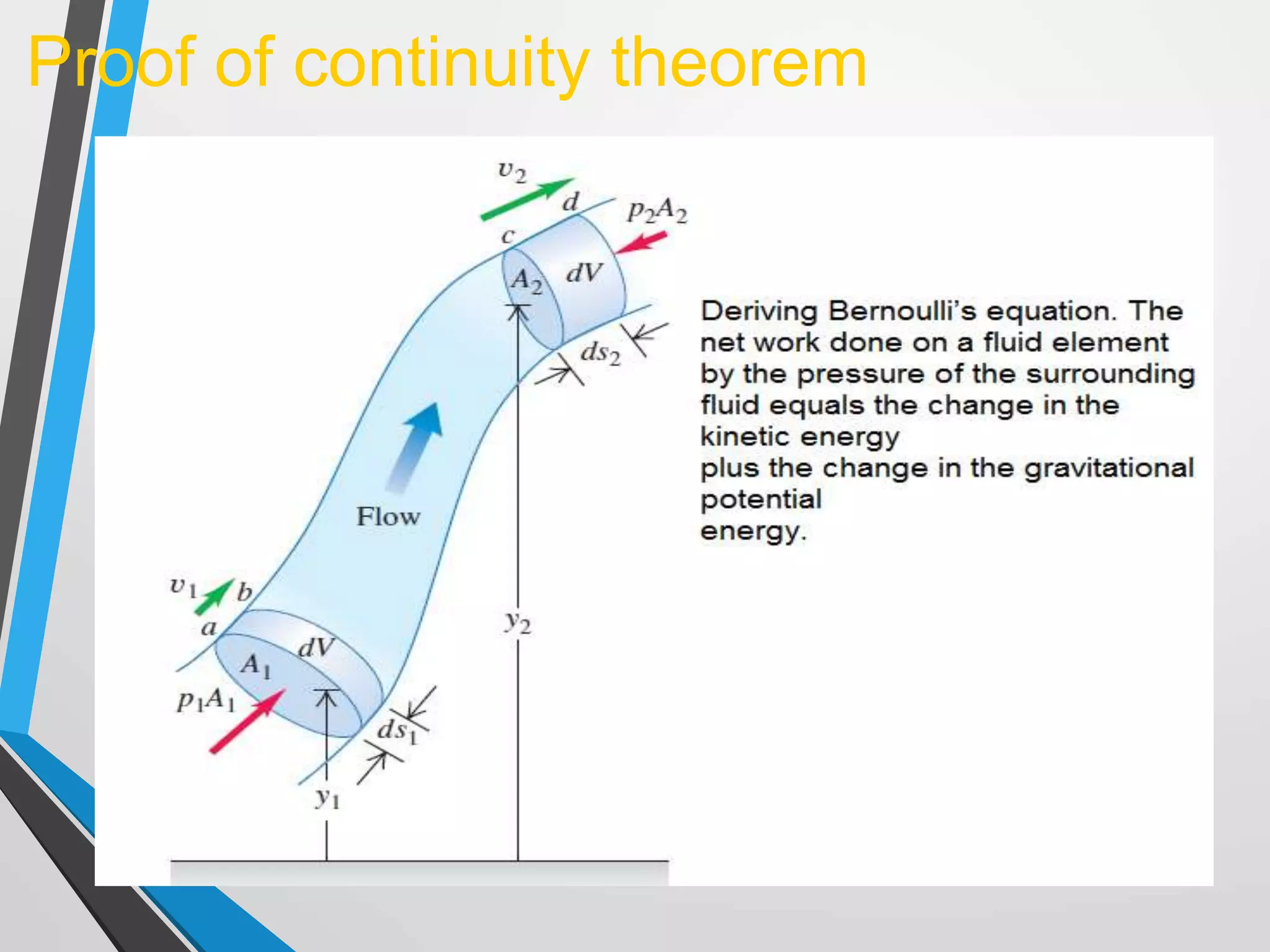
This document discusses Bernoulli's principle and equation in fluid mechanics. It provides definitions and explanations of key terms like Bernoulli's principle, conservation of energy principle, and various forms of Bernoulli's equation. It also includes proofs of Bernoulli's theorem derived from conservation of energy and Newton's second law. Finally, it discusses the continuity equation and theorem in fluid mechanics.

1. Fluid Mechanics
Mechanical Engineering department
Created by:
Manthan Kanani
Manthan kanani 140050119028
Ishant kalra 140050119027
BITs edu campus

2. Bernoulli's Equation
In fluid dynamics, Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a
decrease in the fluid's potential energy.The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738.
Bernoulli's principle can be applied to various types of fluid flow, resulting in various forms of Bernoulli's equation; there are different
forms of Bernoulli's equation for different types of flow.The simple form of Bernoulli's equation is valid for incompressible flows
Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of energy in a
fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy, potential energy and internal energy
remains constant. Thus an increase in the speed of the fluid – implying an increase in both its dynamic pressure and kinetic energy – occurs with a
simultaneous decrease in (the sum of) its static pressure, potential energy and internal energy. If the fluid is flowing outof a reservoir, the sum of all
forms of energy is the same on all streamlines because in a reservoir the energy per unit volume (the sum of pressure and gravitational potential ρ g h)
is the same everywhere.
Bernoulli's principle can also be derived directly from Newton's 2nd law. If a small volume of fluid is flowing horizontally from a region of
high pressure to a region of low pressure, then there is more pressure behind than in front.This gives a net force on the volume,
accelerating it along the streamline.
Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline,
where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of
lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher
pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed
occurs where the pressure is highest.

3. Bernoulli's Equation
In continuum mechanics there are two laws to attention.
Conservation
Energy
Mass
Momentum
Inequalities
Entropy
In fluid mechanics we should be keep mind on this given member of liquid, gas.
FLUID - Statics · DynamicsArchimedes' principle · Bernoulli's principle Navier–Stokes equations poiseuille
equation · Pascal's lawViscosity (Newtonian · non-Newtonian) Buoyancy · Mixing · Pressure.
LIQUID - Surface tension Capillary action
GAS -Atmosphere Boyle's law Charles's law Gay-Lussac's law Combined gas law.

4. Proof of Bernoulli’s theorem
where F denotes a force and an x a displacement.
The second term picked up its negative sign
because the force and displacement are in opposite
directions.
We examine a fluid section of mass m traveling
to the right as shown in the schematic above.
The net work done in moving the fluid is
.......Eq.(1)

5. Proof of Bernoulli’s theorem
Pressure is the force exerted over the cross-sectional area, or P = F/A.
Rewriting this as F = PA and substituting into Eq.(1) we find that
The displaced fluid volume V is the cross-sectional area A times the
thickness x.This volume remains constant for an incompressible fluid, so
Eq.(3)
Eq.(2)
Using Eq.(3) in Eq.(2) we have
Eq.(4)

6. Proof of Bernoulli’s theorem
Since work has been done, there has been a change in the mechanical energy of
the fluid segment.This energy change is found with the help of the next diagram.
The energy change between the
initial and final positions is given by
.......Eq.(5)
Here, the the kinetic energy K =
mv²/2 where m is the fluid mass
and v is the speed of the fluid.The
potential energy U = mgh where g is
the acceleration of gravity, and h is
average fluid height.

7. The work-energy theorem says that the net work done is equal to the
change in the system energy.This can be written as
Proof of Bernoulli’s theorem
Eq.(6)
Substitution of Eq.(4) and Eq.(5) into Eq.(6) yields
Eq.(7)
Dividing Eq.(7) by the fluid volume, V gives us
Eq.(8)
where
Eq.(9)

8. Proof of Bernoulli’s theorem
is the fluid mass density.To complete our derivation, we reorganize Eq.(8).
Eq.(10)
Finally, note that Eq.(10) is true for any two positions.Therefore,
Eq.(11)
Equation (11) is commonly referred to as Bernoulli's equation. Keep in mind
that this expression was restricted to incompressible fluids and smooth fluid
flows.

9. A continuity equation in physics is an equation that describes the transport of some
quantity. It is particularly simple and particularly powerful when applied to a conserved
quantity, but it can be generalized to apply to any extensive quantity.
Since mass,energy, momentum, electric charge and other natural quantities are
conserved under their respective appropriate conditions, a variety of physical
phenomena may be described using continuity equations.
continuity theorem
Continuity equations are a stronger, local form of conservation laws. For example,
a weak version of the law of conservation of energy states that energy can neither
be created nor destroyed—i.e., the total amount of energy is fixed.This statement
does not immediately rule out the possibility that energy could disappear from a
field in Canada while simultaneously appearing in a room in Indonesia. A stronger
statement is that energy is locally conserved: Energy can neither be created nor
destroyed, nor can it "teleport" from one place to another—it can only move by a
continuous flow.A continuity equation is the mathematical way to express this
kind of statement. For example, the continuity equation for electric charge states
that the amount of electric charge at any point can only change by the amount
of electric current flowing into or out of that point.

10. Continuity equations more generally can include "source" and "sink" terms, which allow
them to describe quantities that are often but not always conserved, such as the density
of a molecular species which can be created or destroyed by chemical reactions. In an
everyday example, there is a continuity equation for the number of people alive; it has a
"source term" to account for people being born, and a "sink term" to account for people
dying.
continuity theorem
Any continuity equation can be expressed in an "integral form" (in terms of
a flux integral), which applies to any finite region, or in a "differential form"
(in terms of the divergence operator) which applies at a point.

11. Proof of continuity theorem

12. Proof of continuity theorem
-Streamlines represent a trajectory and do not meet or cross
-Velocity vector is tangent to streamline
-Volume of fluid follows a tube of flow bounded by streamlines
-Streamline density is proportional to velocity
Flow obeys continuity equation
Volume flow rate (𝑚3 /s) Q = A·v (
𝑚2
x m / s ) is constant along flow
tube.
A1v1 = A2v2

13. • KaNaNi MaNtHaN 140050119028
• IsHaNt KaLrA 140050119027