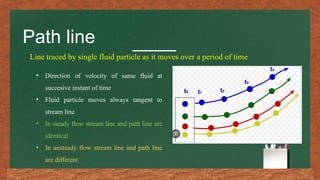
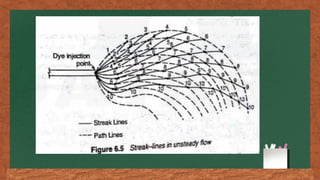
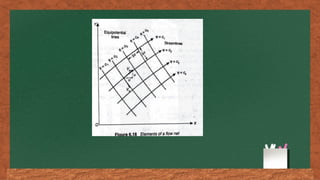
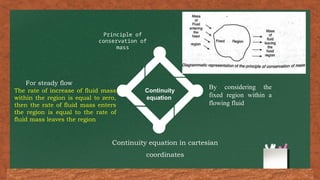
The document discusses fluid flow patterns, defining key concepts like streamlines, pathlines, and streaklines, which illustrate the direction of fluid velocity at various points. It explains the differences between steady and unsteady flow, as well as introduces concepts like stream tubes, flow nets, equipotential lines, and the continuity equation. It emphasizes the fundamental principles governing fluid dynamics including conservation of mass, energy, and momentum.

1. Description of flow pattern

2. Stream line
01
02 Pattern of flow of fluid may be represented by series
of stream line obtained by drwaing a series of curves
through the flowing fluid such that velocity vector at
any point is tangential to the curve
Imaginary curve drawn through a
flowing fluid in such a way that the
tangent to it at any point gives the
direction of velocity of flow at that
point

4. Stream
line
01
02
03
04
stream line remains same for
different time
Steady flow
stream line changes for every
instance
Unsteady flow
No component of
velocity at right
angle to stream
line
No flow of fluid
across any stream
line

5. Stream tube
01
02
• No flow across the stream tube.
• Fluid may enter or leave the tube only at its
end.
• Stream tube with cross sectional area small
enough for the variation of velocity over it to
be negligible is refreed as stream filament.
Imaginary tube formed by group of
stream line passing through a small
closed curve, which may or may not be
a circular.

6. Path line
• Direction of velocity of same fluid at
succesive instant of time
• Fluid particle moves always tangent to
stream line
• In steady flow stream line and path line are
identical
• In unsteady flow stream line and path line
are different
Line traced by single fluid particle as it moves over a period of time

7. Streak line
• Direction of velocity of same fluid at
succesive instant of time
• Fluid particle moves always tangent to
stream line
• In steady flow streak line, stream line and
path line are identical
Line traced by a fluid particle passing through a fixed point in a flow field

9. Flow net
A grid obtained by drawing a series of streamlines and equipotential lines
• It can be drawn for two
dimensional irrotational flow
• Provides info about flow
pattern

10. Flow net
A grid obtained by drawing a series of streamlines and equipotential lines
• It can be drawn for two
dimensional irrotational flow
• Provides info about flow
pattern

12. Equipotential line
, Ψ= constant represents a curve for which the velocity potential is same at every
ɸ
point, represents an equipotential line

13. Velocity potential
It is scalar function of space and time such that its negative derivation with respect
to any direction gives the fluid velocity in that direction.
= f(x,y,z,t) - unsteady flow
ɸ
= f(x,y,z,) - steady flow
ɸ
Velocity potential
exists only for
irrotational flow

14. Stream function
It is scalar function of space and time, such that its partial derivative with respect to
any direction gives the velocity component at right angle to this direction.
= f(x,y,t) - unsteady flow
ɸ
= f(x,y,) - steady flow
ɸ
Stream function
exists only if
flow satisfies
continuity
equation

15. Basic principles of
fluid flow
• Principle of conservation of mass
• Principle of conservation of energy
• Principle of conservation of momentum

16. Continuity
equation
Principle of
conservation of
mass
Continuity equation in cartesian
coordinates
For steady flow
By considering the
fixed region within a
flowing fluid
The rate of increase of fluid mass
within the region is equal to zero,
then the rate of fluid mass enters
the region is equal to the rate of
fluid mass leaves the region

20. 01 02 03 04
Click here to add content
of the text the main idea
of this page,
Enter title
Click here to add content
of the text the main idea
of this page,
Enter title
Click here to add content
of the text the main idea
of this page,
Enter title
Click here to add content
of the text the main idea
of this page,
Enter title

21. Enter title Enter title Enter title Enter title
Click here to add content
of the text the main idea
of this page,
Click here to add content
of the text the main idea
of this page,
Click here to add content
of the text the main idea
of this page,
Click here to add content
of the text the main idea
of this page,