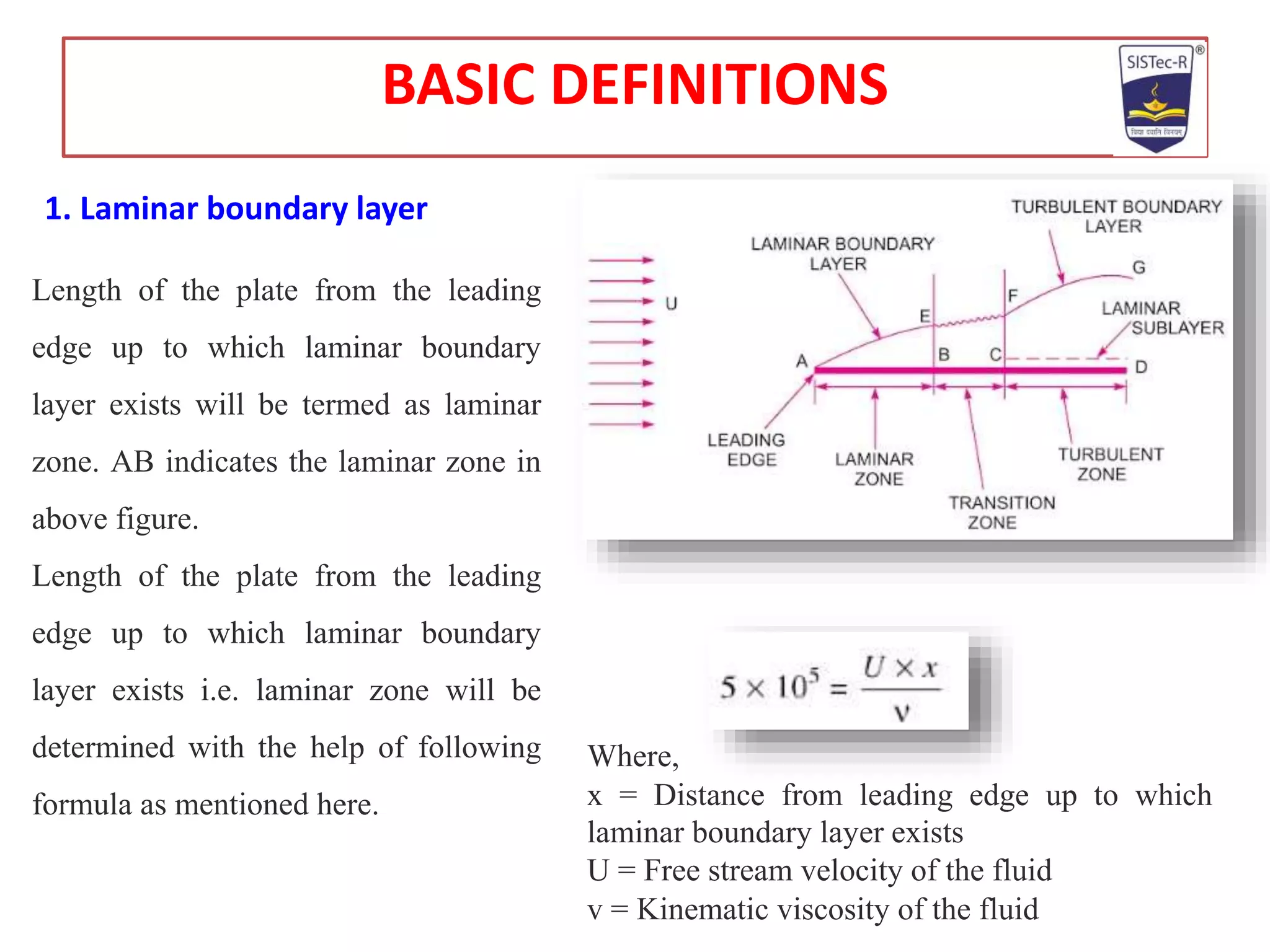
This document provides an introduction to boundary layer theory in fluid mechanics. It defines key terms like boundary layer thickness, displacement thickness, and momentum thickness. The boundary layer is a thin region near a solid surface where velocity gradients exist due to no-slip conditions. As fluid flows over a plate, the boundary layer transitions from laminar to turbulent flow. Boundary layer theory divides fluid flow into the boundary layer region with velocity gradients and an external region with nearly uniform free stream velocity.

1. FLUID MECHANICS
BOUNDARY LAYER THEORY
LECTURE-01
CONTENTS:-
1. Introduction to boundary layer theory
2. Basic Definitions
3. Boundary layer Thickness
PROF. SANJEEV GUPTA

2. INTRODUCTION TO BOUNDARY LAYER
 When a real fluid will flow over a solid body or a
solid wall, the particles of fluid will adhere to the
boundary and there will be condition of no-slip.
 If we assume that boundary is stationary or
velocity of boundary is zero, then the velocity
of fluid particles adhere or very close to the
boundary will also have zero velocity.
 If we move away from the boundary, the velocity of fluid particles will also be
increasing. Velocity of fluid particles will be changing from zero at the surface of
stationary boundary to the free stream velocity (U) of the fluid in a direction normal
to the boundary.

3. INTRODUCTION TO BOUNDARY LAYER
 Therefore, there will be presence of velocity gradient
(du/dy) due to variation of velocity of fluid particles.
 The variation in the velocity of the fluid particles,
from zero at the surface of stationary boundary to the
free stream velocity (U) of the fluid, will take place
in a narrow region in the vicinity of solid boundary
and this narrow region of the fluid will be termed as
boundary layer.
 Science and theory dealing with the problems of boundary layer flows will be termed
as boundary layer theory.
 According to the boundary layer theory, fluid flow around the solid boundary might be
divided in two regions as mentioned and displayed here in following figure.

4. First region
A very thin layer of fluid, called the boundary layer, in the immediate region of the solid
boundary, where the variation in the velocity of the fluid particles, from zero at the surface
of stationary boundary to the free stream velocity (U) of the fluid, will take place.
There will be presence of velocity gradient (du/dy) due to variation of velocity of fluid
particles in this region and therefore fluid will provide one shear stress over the wall in the
direction of motion.
Shear stress applied by the fluid over the wall will be determined with the help of following
equation.
𝜏 = µ x (du/dy)
Second region
Second region will be the region outside of the boundary layer. Velocity of the fluid
particles will be constant outside the boundary layer and will be similar with the free stream
velocity of the fluid.
In this region, there will be no velocity gradient as velocity of the fluid particles will be
constant outside the boundary layer and therefore there will be no shear stress exerted by
the fluid over the wall beyond the boundary layer.

5. 1. Laminar boundary layer
BASIC DEFINITIONS
Length of the plate from the leading
edge up to which laminar boundary
layer exists will be termed as laminar
zone. AB indicates the laminar zone in
above figure.
Length of the plate from the leading
edge up to which laminar boundary
layer exists i.e. laminar zone will be
determined with the help of following
formula as mentioned here.
Where,
x = Distance from leading edge up to which
laminar boundary layer exists
U = Free stream velocity of the fluid
v = Kinematic viscosity of the fluid

6. 2.Turbulent boundary layer fundamentals
If the length of plate is greater than the value of x which is determined from above equation,
thickness of boundary layer will keep increasing in the downstream direction.
Laminar boundary layer will become unstable and movement of fluid particles within it will
be disturbed and irregular. It will lead to a transition from laminar to turbulent boundary
layer.
This small length over which the boundary layer flow changes from laminar to turbulent will
be termed as transition zone. BC, in above figure, indicates the transition zone.
Further downstream the transition zone, boundary layer will be turbulent and the layer of
boundary will be termed as turbulent boundary layer.
FG, in above figure, indicates the turbulent boundary layer and CD represent the turbulent
zone.

7. Boundary layer thickness
Boundary layer thickness is basically defined as the distance from the surface of the
solid body, measured in the y-direction, up to a point where the velocity of flow is 0.99
times of the free stream velocity of the fluid.
Boundary layer thickness will be displayed by the symbol δ.
We can also define the boundary layer thickness as the distance from the surface of the
body up to a point where the local velocity reaches to 99% of the free stream velocity of
fluid. For laminar and turbulent zone it is denoted as
BOUNDARY LAYER THICKNESS

8. Displacement thickness
Displacement thickness is basically defined as the distance, measured perpendicular to the
boundary of the solid body, by which the boundary should be displaced to compensate for
the reduction in flow rate on account of boundary layer formation.
Displacement thickness will be displayed by the symbol δ*.
We can also define the displacement thickness
as the distance, measured perpendicular to the
boundary of the solid body, by which the free
stream will be displaced due to the formation of
boundary layer

9. Momentum thickness
Momentum thickness is basically defined as the distance, measured perpendicular to the
boundary of the solid body, by which the boundary should be displaced to compensate for the
reduction in momentum of the flowing fluid on account of boundary layer formation.
Momentum thickness will be displayed by the symbol θ.
Energy thickness
Energy thickness is basically defined as the distance, measured perpendicular to the
boundary of the solid body, by which the boundary should be displaced to compensate for
the reduction in kinetic energy of the flowing fluid on account of boundary layer formation.
Energy thickness will be displayed by the symbol δ**.

10. Applications of Boundary Layer