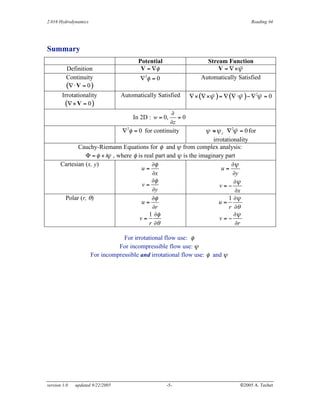
Potential flow theory assumes flows are inviscid and irrotational. A potential function φ can be defined to represent the velocity field, satisfying continuity and irrotationality. The Laplace equation governs φ. Potential and streamlines are perpendicular. Simple flows include uniform flow, source/sink, and vortex flows, with characteristic potential functions. The Bernoulli equation relates pressure, velocity, and elevation for steady, inviscid flows.