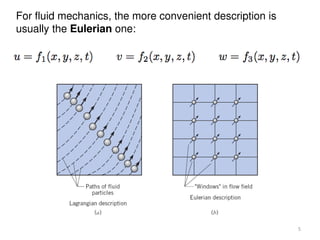
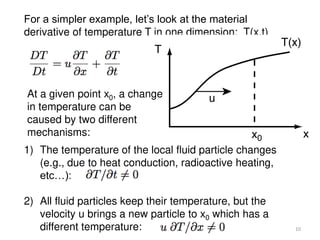
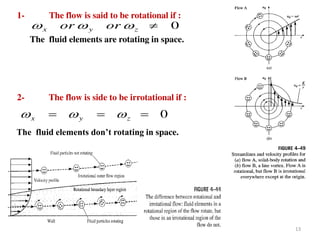
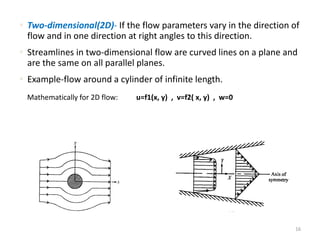
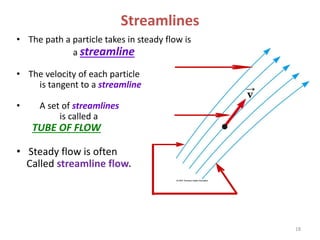
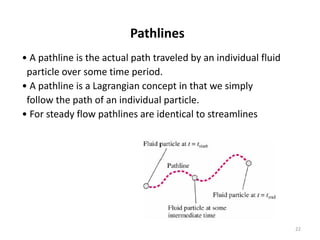
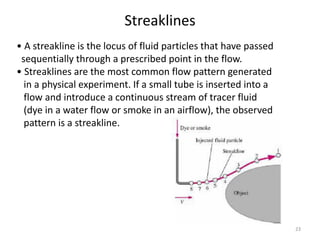
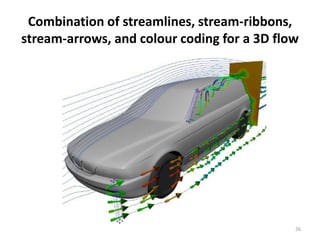
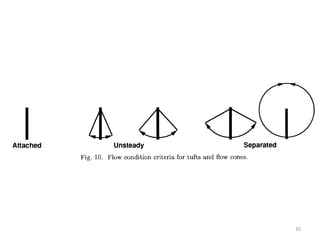
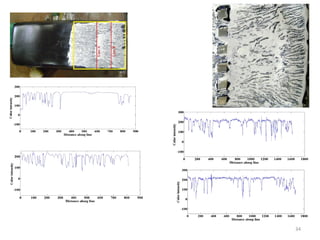
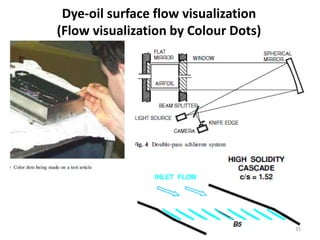
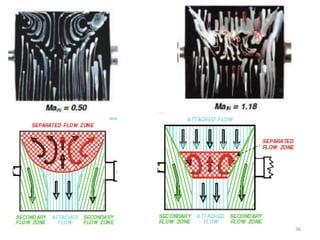
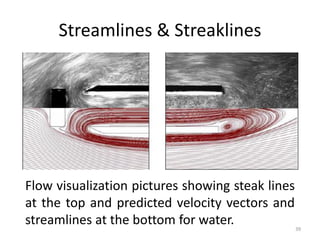
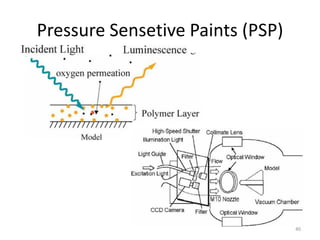
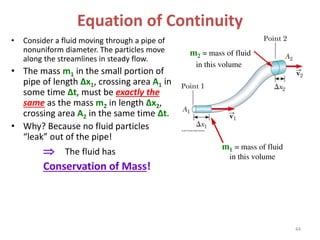
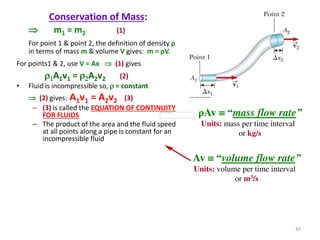
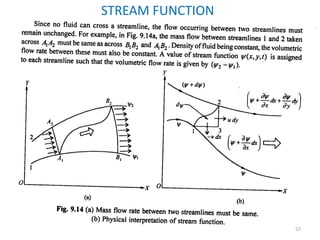
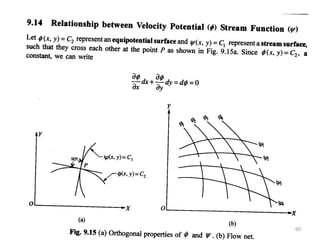
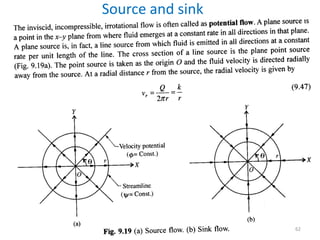
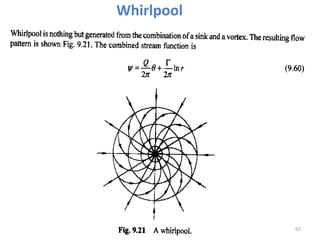
The document covers fluid kinematics, detailing the differences between steady and unsteady flows, uniform and non-uniform flows, and two main descriptions of fluid motion: Lagrangian and Eulerian. It explains the concepts of streamlines, pathlines, streaklines, and the equation of continuity in fluid dynamics, emphasizing conservation of mass in fluid systems. Various visualization techniques and representations of flow patterns are also discussed, including the use of stream tubes and different flow conditions.

1. 1
Akshoy Ranjan Paul
Associate Professor
Email: arpaul2k@gmail.com
DEPARTMENT OF APPLIED MECHANICS
MOTI LAL NEHRU NATIONAL INSTITUTE OF TECHNOLOGY
ALLAHABAD
Fluid Mechanics and Hydraulic Machines
(AMN13104)
B Tech. Mechanical Engg. (3rd semester)
Chapter-3: Fluid Kinematics

2. Steady and Unsteady Flows
Steady Flow: The fluid variables(such as velocity,pressure,density,temperature)
at a given point in space does not vary with time. In other words, the time rate of
the dependent variables at a position is zero.
Unsteady Flow: The fluid variables(such as V,P,d,T etc) at a given point in space
does vary with time.
Almost all flows have some unsteadiness. In addition, there are periodic
flows, non-periodic flows, and completely random flows.
Very often, we assume steady flow conditions for cases where there is only
a slight time dependence, since the analysis is “easier”.
2

3. uniform flow: If the velocity, in magnitude, direction and sense, is
identical throughout the flow field. Means the velocity
components to be the same at different position in the flow
field.
non-uniform: If the velocity components at different locations are
different at the same instant of time, the flow is said to
be non-uniform.
Uniform and non-uniform flow
3

4. Lagrangian and Eulerian Descriptions of Fluid Motion
Eulerian: Observer stays at a fixed point in space.
Lagrangian: Observer moves along with a given fluid particle.
We consider first the Lagrangian case. The position of a
fluid particle at a given time t can be written as a Cartesian
vector
For a complete description of a flow, we need to know
at every point. Usually one references each particle to its
initial position:
4

5. For fluid mechanics, the more convenient description is
usually the Eulerian one:
5

6. Acceleration: Normal and Tangential Components
Velocity can be written as:
where V(s,t) is the speed and
is a unit vector tangential
to the velocity.
The derivative of the speed is (since ds/dt = V):
6

7. The time derivative of the unit vector is non-zero because the
direction of the unit vector changes. The centripetal
acceleration is
so that the total acceleration becomes
7

8. Acceleration in Cartesian Coordinates
This is probably one of the most fundamental concepts of
the course, but it is not very intuitive!
or
8

9. From last page, we
had
This derivative is called the full derivative or material
derivative.
It is often written D/Dt instead of d/dt.
It can apply to other quantities as well.
9

10. For a simpler example, let’s look at the material
derivative of temperature T in one dimension: T(x,t)
At a given point x0, a change
in temperature can be
caused by two different
mechanisms:
1) The temperature of the local fluid particle changes
(e.g., due to heat conduction, radioactive heating,
etc…):
2) All fluid particles keep their temperature, but the
velocity u brings a new particle to x0 which has a
different temperature: 10

11. The changes are called “local change” and “convective
change” (the convective change is also called “advective
change”)
= local temperature change
= local acceleration in x
= convective temperature change
= convective acceleration in x
11

12. The rate of rotation can be expressed or equal to the angular velocity
vector or the ROTATION vector ( ):
Note:








































y
u
x
v
x
w
z
u
z
v
y
w
z
y
x
2
1
2
1
2
1




k
y
u
x
v
j
x
w
z
u
i
z
v
y
w








































2
1
2
1
2
1

Rotational and Irrotational Flow
Rotational ( ):

12

13. 1- The flow is said to be rotational if :
0

z
y
x or
or 


2- The flow is side to be irrotational if :
0


 z
y
x 


The fluid elements are rotating in space.
The fluid elements don’t rotating in space.
13

14. Vorticity ( ξ ):
Vorticity is a measure of rotation of a fluid particle.
Vorticity is twice the angular velocity of a fluid particle.








































y
u
x
v
x
w
z
u
z
v
y
w
z
y
x



14

15.  one dimensional(1D)- if the flow parameters (such as velocity,
pressure, depth etc.) at a given instant in time only vary in the
direction of flow and not across the cross-section. The flow
may be unsteady, in this case the parameter vary in time but
still not across the cross-section.
Example- flow is the flow in a pipe.
One, Two or Three-dimensional Flow
Mathematically for 1D: U=f(x) , v=o , w=o
15

16.  Two-dimensional(2D)- If the flow parameters vary in the direction of
flow and in one direction at right angles to this direction.
 Streamlines in two-dimensional flow are curved lines on a plane and
are the same on all parallel planes.
 Example-flow around a cylinder of infinite length.
Mathematically for 2D flow: u=f1(x, y) , v=f2( x, y) , w=0
16

17. Three-Dimensional Flow(3D) - That type of flow in which the velocity is a function of time and
three mutually perpendicular directions. But for a steady 3D flow the flow parameters are
Function of space co-ordinates (x, y& z) only.
Mathematically for 3D flow: U=f1(x, y, z) , v=f2(x, y, z) and w=f3(x, y, z)
17

18. Streamlines
• The path a particle takes in steady flow is
a streamline
• The velocity of each particle
is tangent to a streamline
• A set of streamlines
is called a
TUBE OF FLOW
• Steady flow is often
Called streamline flow.
18

19. Some things to know about streamlines:
 Because the fluid is moving in the same direction as the
streamlines, fluid can not cross a streamline.
 Streamlines can not cross each other. If they were to cross
this would indicate two different velocities at the same
point. This is not physically possible.
 The above point implies that any particles of fluid starting on
one streamline will stay on that same streamline throughout
the fluid.
19

20.  A useful technique in fluid flow analysis is to consider only a
part of the total fluid in isolation from the rest.
 This can be done by imagining a tubular surface formed by
streamlines along which the fluid flows.
 This tubular surface is known as a stream tube.
 In a two-dimensional flow, we have a stream tube which is
flat (in the plane of the paper).
Stream tubes
A stream tube 20

21. • The "walls" of a stream tube are made of streamlines.
• As we have seen above, fluid cannot flow across a streamline, so
fluid cannot cross a stream tube wall.
• The stream tube can often be viewed as a solid walled pipe.
• A stream tube is not a pipe - it differs in unsteady flow as the walls
will move with time. And it differs because the "wall" is moving
with the fluid.
21

22. Pathlines
• A pathline is the actual path traveled by an individual fluid
particle over some time period.
• A pathline is a Lagrangian concept in that we simply
follow the path of an individual particle.
• For steady flow pathlines are identical to streamlines
22

23. Streaklines
• A streakline is the locus of fluid particles that have passed
sequentially through a prescribed point in the flow.
• Streaklines are the most common flow pattern generated
in a physical experiment. If a small tube is inserted into a
flow and introduce a continuous stream of tracer fluid
(dye in a water flow or smoke in an airflow), the observed
pattern is a streakline.
23

24. • Streaklines are often confused with streamlines or pathlines.
• While the three flow patterns are identical in steady flow,
they can be quite different in unsteady flow.
• The main difference is that a streamline represents an
instantaneous flow pattern at a given instant in time,
while a streakline and a pathline are flow patterns that
have some age and thus a time history associated with
them.
• A streakline is an instantaneous snapshot of a time
integrated flow pattern.
• A pathline, on the other hand, is the time-exposed flow
path of an individual particle over some time period.
24

25. Flow Visualization on Car
25

26. Combination of streamlines, stream-ribbons,
stream-arrows, and colour coding for a 3D flow
26

27. Surface Flow Visualization
1. Tuft Flow visualization
27

28. 28

29. Car @ 0 w.r.t. flow
29

30. 30

31. Car @ +10 w.r.t. flow
@ 10 m/s @ 20 m/s
@ 30 m/s @ 30 m/s (close view)
31

32. Study of Rear wakes of car
@ 20 m/s @ 30 m/s 32

33. Surface Flow Visualization
2. Oil Flow visualization
33

34. 34

35. Dye-oil surface flow visualization
(Flow visualization by Colour Dots)
35

36. 36

37. Smoke Flow Visualization
37

38. Car without Rear Spoiler
Car with Rear Spoiler 38

39. Streamlines & Streaklines
Flow visualization pictures showing steak lines
at the top and predicted velocity vectors and
streamlines at the bottom for water. 39

40. Pressure Sensetive Paints (PSP)
40

41. Schlieren photographs
PSP Measurement
Test Model
41

42. The Equation of Continuity
Q: Have you ever used your thumb to control the water flowing
from the end of a hose?
A: When the end of a hose is partially closed off, thus reducing
its cross-sectional area, the fluid velocity increases.
This kind of fluid behavior is described by the equation of
continuity. 42

43. Equation of Continuity
43

44. • Consider a fluid moving through a pipe of
nonuniform diameter. The particles move
along the streamlines in steady flow.
• The mass m1 in the small portion of
pipe of length Δx1, crossing area A1 in
some time Δt, must be exactly the
same as the mass m2 in length Δx2,
crossing area A2 in the same time Δt.
• Why? Because no fluid particles
“leak” out of the pipe!
 The fluid has
Conservation of Mass!
Equation of Continuity
m1 = mass of fluid
in this volume
m2 = mass of fluid
in this volume
44

45. Conservation of Mass:
 m1 = m2 (1)
For point 1 & point 2, the definition of density ρ
in terms of mass m & volume V gives: m = ρV.
For points1 & 2, use V = Ax  (1) gives
r1A1v1 = r2A2v2 (2)
• Fluid is incompressible so, r = constant
 (2) gives: A1v1 = A2v2 (3)
– (3) is called the EQUATION OF CONTINUITY
FOR FLUIDS
– The product of the area and the fluid speed
at all points along a pipe is constant for an
incompressible fluid
ρAv  “mass flow rate”
Units: mass per time interval
or kg/s
Av  “volume flow rate”
Units: volume per time interval
or m3/s
45

46. • Mass flow rate (mass of fluid passing a point
per second) is constant: ρ1A1v1 = ρ2A2v2
 Equation of Continuity
PHYSICS: Conservation of Mass!!
• For an incompressible fluid (ρ1 = ρ2 = ρ)
Then  A1v1 = A2v2
Or: Av = constant
 Where cross sectional area A is large, velocity
v is small, where A is small, v is large.
• Volume flow rate: (V/t) = A(x/t) = Av
46

47. Implications of Equation of Continuity
A1v1 = A2v2
 The fluid speed v is low where the
pipe is wide (large A)
 The fluid speed v is high where the
pipe is constricted (small A)
• The product, Av, is called the
volume flow rate or flux.
Av = constant says that the volume
that enters one end of the pipe in a
given time equals the volume leaving
the other end in the same time (If no
leaks are present!)
47

48. • PHYSICS: Conservation of Mass!!
A1v1 = A2v2 Or Av = constant
• Small pipe cross section  larger v
• Large pipe cross section  smaller v
48

49. CONTINUITY EQUATION- DIFFERENTIAL FORM
(3D)
In order to derive the continuity equation at a point
in a fluid, the point is enclosed by an elementary
control volume appropriate to the co-ordinate
system and the efflux of mass Across each surface
as well as the rate of accumulation within the
control volume is considered. A rectangular
paralleopiped as shown in the figure 9.7 is the
control volume in the Cartesian co-ordinates system.
Assuming that the fluid enters the face ‘ABCD’ with
a velocity ‘u’ and leaves the face ‘EFGH’ with a
49

50. 50

51. 51

52. 52

53. In vector form
53

54. IRROTATIONAL FLOW
54

55. 55

56. 56

57. STREAM FUNCTION
57

58. 58

59. 59

60. 60

61. 61

62. Source and sink
62

63. Whirlpool
63