1. The curve passes through the origin as there is no constant term in the equation. To find the tangents at the origin, the lowest degree terms are equated to zero, giving the x-axis as a tangent. 2. The curve meets the coordinate axes only at the origin. There are no other points of intersection. 3. The curve is symmetric about the x-axis as the powers of y in the equation are even. There are no other symmetries. 4. The y-axis is the only asymptote, obtained by equating the coefficient of the highest power of y to zero. There is no asymptote parallel to the x-axis. 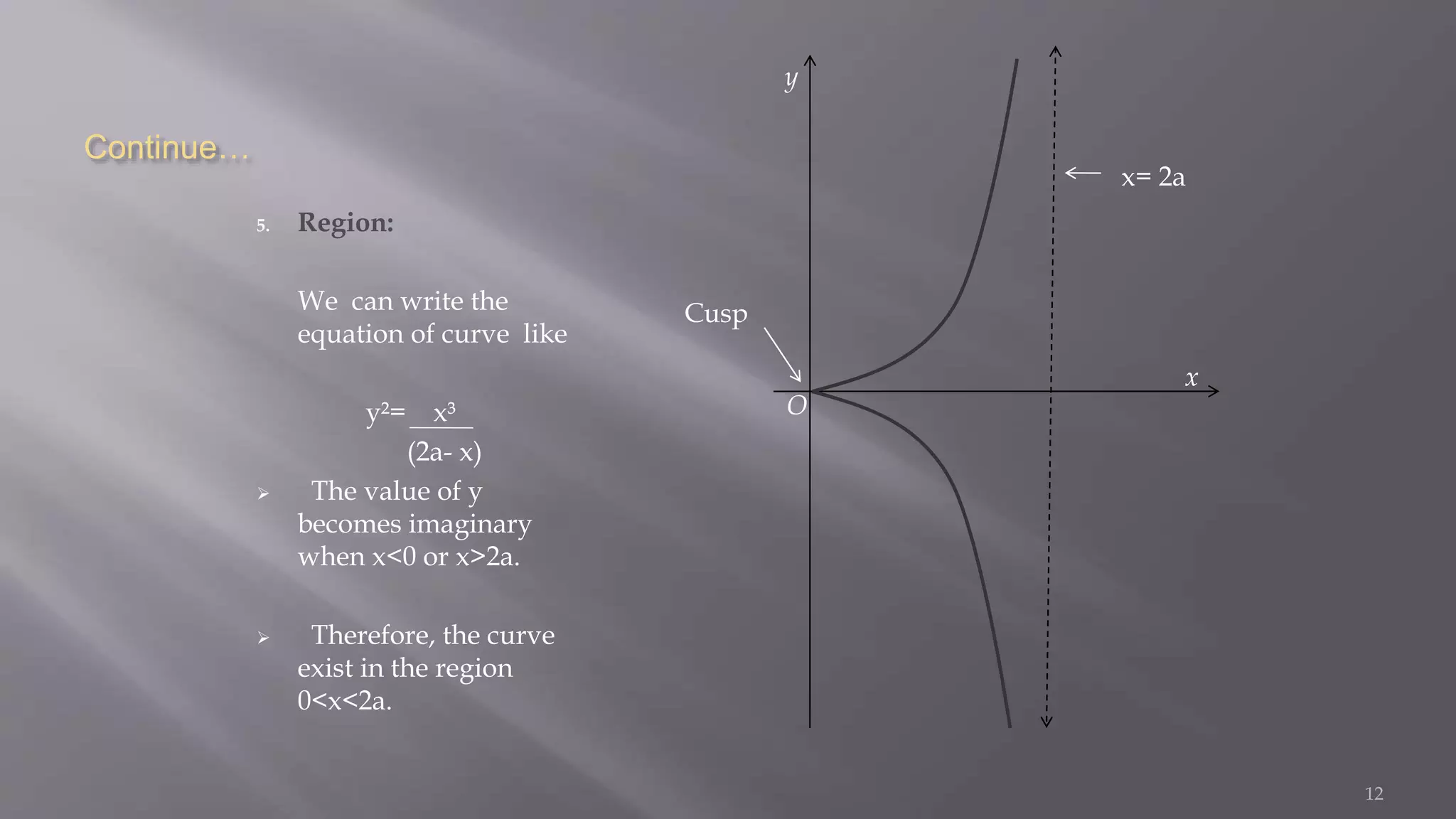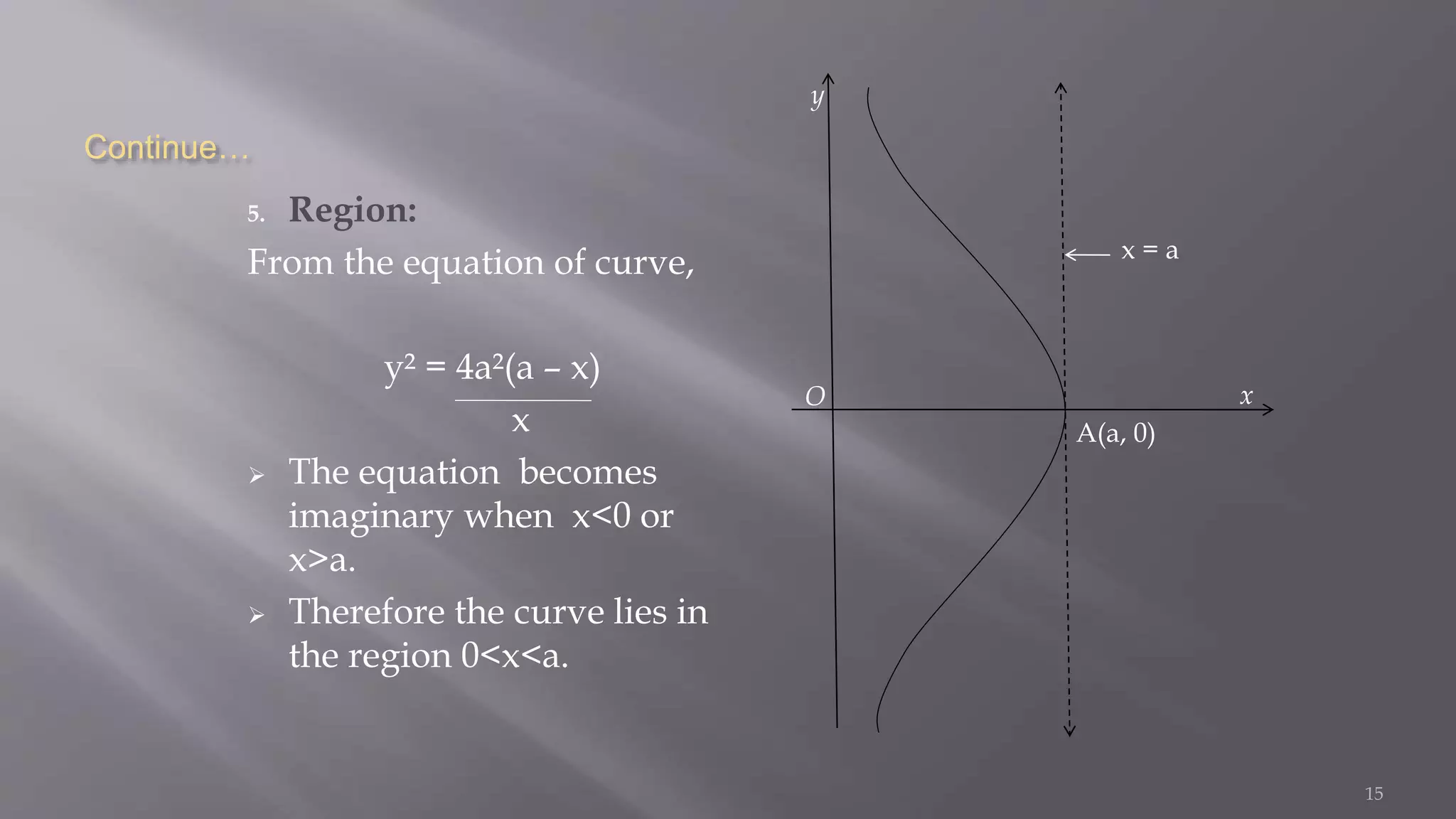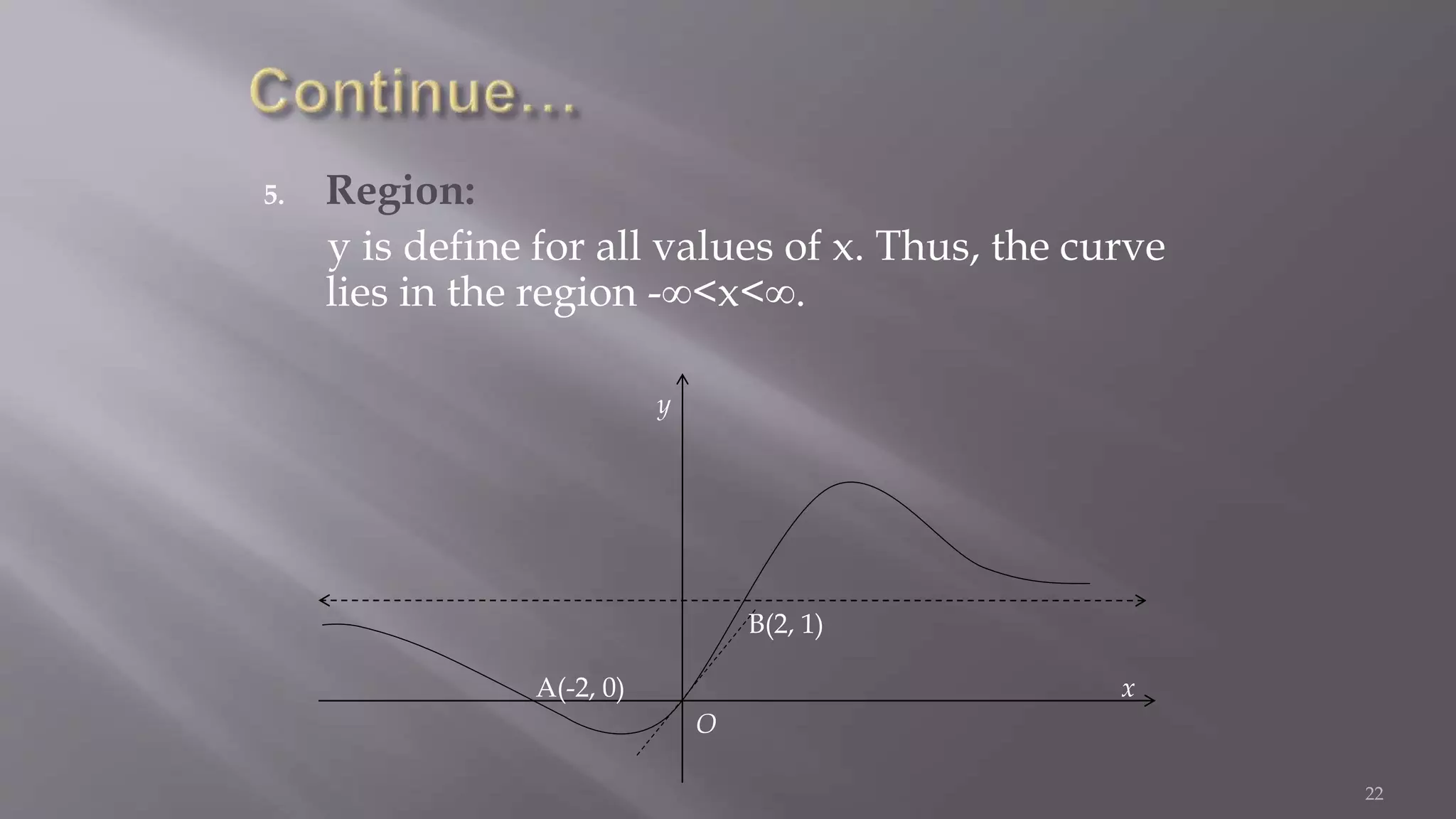5. The curve exists in

1. By Kaushal Patel

2.  The curve is symmetric about x-axis if the power of y
occurring in the equation are all even, i.e. f(x,-y)=f(x, y).
 The curve is symmetric about y-axis if the powers of x
occurring in equation are all even, i.e. f(-x, y)=f(x, y).
2

3.  The curve is symmetric about the line y= x, if on
interchanging x and y, the equation remains unchanged,
i.e. f(y, x)=f(x, y).
 The curve is symmetric in opposite quadrants or about
origin if on replacing x by –x by y by –y, the equation
remains unchanged, i.e. f(-x,-y)=f(x, y).
3

4.  The curve passes through the origin if there is no constant term
in the equation.
 If curve passes through the origin, the tangents at the origin are
obtained by equating the lowest degree term in x and y to zero.
 If there are two or more tangents at the origin, it is called a node,
a cusp or an isolated point if the tangents at this point are real
and distinct, real and coincident or imaginary respectively.
4

5.  The point of intersection of curve with x and y axis are
obtained by putting y=0 and x=0 respectively in the
equation of the curve.
 Tangent at the point of intersection is obtained by
shifting the origin to this point and then equating the
lowest degree term to zero.
5

6.  Cusps: If tangents are real and coincident then the double point is called
cusp.
 Nodes: If the tangents are real and distinct then the double point is called
node.
 Isolated Point: If the tangents are imaginary then double point is called
isolated point.
6

7.  Asymptotes parallel to x-axis are obtain by equating the
coefficient of highest degree term of the equation to
zero.
 Asymptotes parallel to y-axis are obtained by equating
the coefficient of highest degree term of y in the
equation to zero.
7

8.  Oblique asymptotes are obtained by the following method:
Let y= mx + c is the asymptote to the curve and 2(x, y), 3(x, y) are
the second and third degree terms in equation.
Putting x=1 and y=m in 2(x, y) and 3(x, y)
2(x, y)= 2(1, m) or 2(m)
3(x, y)= 3(1, m) or 3(m)
Find c=-( 2(m)/ ’3(m))
Solve 3(m)=0
m=m1,m2,……
8

9.  This region is obtained by expressing one variable in terms of
other, i.e., y=f(x)[or x=f(y)] and then finding the values of x (or y)
at which y(or x) becomes imaginary. The curve does not exist in
the region which lies between these values of x (or y).
9

10. 1. Symmetry: The power of y in the equation of curve is even
so the curve is symmetric about x- axis.
2. Origin: The equation of curve dose not contain any constant
term so the curve passes through the origin.
to find tangents at the origin equating lowest
degree term to zero,
2ay²= 0
=> y²= 0
=> y= 0
Thus x-axis be a tangent.
10

11. 3. Points of intersection: Putting y=0, we get x=0. Thus, the curve
meets the coordinate axes only at the origin.
4. Asymptotes:
a) Since coefficient of highest power of is constant, there is no
parallel asymptote to x- axis.
b) Equating the coefficient of highest degree term of y to zero, we
get
2a-x= 0
=>x= 2a is the asymptote parallel to y-axis.
11

12. Continue…
5. Region:
We can write the
equation of curve like
y²= x³
(2a- x)
 The value of y
becomes imaginary
when x<0 or x>2a.
 Therefore, the curve
exist in the region
0<x<2a.
12
y
O
x
x= 2a
Cusp

13. 1. Symmetry: The powers of y is even in equation of
curve so curve is symmetric about x- axis.
2. Origin: The equation of curve contain a constant
term so curve dose not passes through origin.
3. Point of intersection: Putting y=0, we get x= a. Thus
the curve meets the x- axis at (a, 0).
to get tangent at (a, 0), Shifting the origin to (a, 0).
x=a be tangent at the origin.
13

14. 4. Asymptotes:
a) Equating the coefficient of highest power of x to zero,
we get y² +4a² = 0 which gives imaginary values. Thus,
there is no asymptote parallel to x-axis.
b) Equating the coefficient of highest power of y to zero,
we get x = 0. Thus, y-axis be the asymptote.
14

15. Continue…
5. Region:
From the equation of curve,
y² = 4a²(a – x)
x
 The equation becomes
imaginary when x<0 or
x>a.
 Therefore the curve lies in
the region 0<x<a.
15
A(a, 0)
x = a
y
O x

16. 1. Symmetry: The powers of x and y both are even so the curve
is symmetric about both x and y-axis.
2. Origin: By putting point (0, 0) in equation, equation is
satisfied. So, the curve is passes through the origin.
to find tangents at the origin equating lowest degree term to
zero,
-b²x²-a²y² = 0
we get imaginary values. So, the tangents at the origin are
imaginary.
16

17. 3. Point of Intersection and Special Points:
a) Tangents at the origin are imaginary. So, the origin is
isolated point.
b) Curve dose not meet x and y axes.
4. Asymptotes:
a) Equating the coefficient of highest power of x to zero, we get
y²-b² = 0. Thus y=±b are the asymptotes parallel to x- axis.
b) Equating the coefficient of highest power of y to zero, we get
x²-a² = 0. Thus, x=±a are the asymptotes parallel to y-axis.
17

18. Continue…
5. Region:
From the equation of
curve,
y=± bx and x=± ay
√x² -a² √y² -b²
 y is imaginary when –
a<x<a and x is imaginary
when –b<y<b.
 Therefore the curve lies
in the region -∞<x<-a,
a<x<∞ and -∞<y<-b,
b<y<∞.
18
y
x
O
x=-a
x=a
y= b
y= -b

19. 1. Symmetry: The equation of curve is not satisfy any condition of
symmetricity. So, curve is not symmetric.
2. Origin: The equation of curve dose not contain any constant
term. So, curve passes through the origin.
Equating lowest degree term to zero,
4y-2x=0
=>x=2y is tangent at the origin.
19

20. 3. Point of intersection and Special points:
 Putting y=0, we get x=0, -2. Thus, the curve meets the x-axis
at A(-2, 0) and o(0, 0). Shifting the origin to P(-2, 0) by
putting x=X-2, y=Y+0 in the equation of the curve,
Y(X-2)²+4 = (X-2)²+2(X-2)
=>Y(X²-4X+8)=X²+6X
Equating lowest degree term to zero,
8Y-6X=0
=>4y-3x-6=0 is a tangent at (-2, 0).
 Curve dose not contain any special points.
20

21. 4. Asymptotes:
a) Equating the coefficient of highest degree of x to zero, we get
y-1=0
Thus y=1 is asymptote parallel to x-axis.
b) Equating the coefficient of highest power of y to zero, we get x²
+ 4 = 0 which gives imaginary number . Thus, there is no
asymptote parallel to y-axis.
21

22. 5. Region:
y is define for all values of x. Thus, the curve
lies in the region -∞<x<∞.
22
B(2, 1)
O
A(-2, 0)
y
x

23.  www.tatamcgrawhill.com
23

24. 24