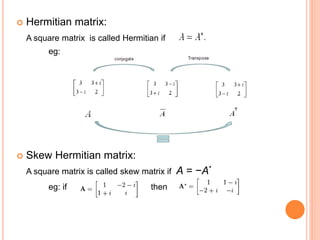
The document presents an overview of matrices, defining various types such as row matrices, column matrices, zero matrices, diagonal matrices, and others, alongside their applications in fields like graph theory and computer graphics. It elaborates on key concepts including the trace, transpose, determinant, singularity, and special types of matrices like symmetric, skew-symmetric, and hermitian matrices. Additionally, it introduces crucial properties of these matrices, such as the conditions for unitary and orthogonal matrices.

1. Presentation
on
Matrices and some
special matrices
In partial fulfillment of the subject
Vector calculus and linear algebra
(2110015)
Submitted by:
Agarwal Ritika (130120116001) /IT/C-1
Akabari Nirali (130120116002) /IT/C-1
Akanksha Sharma (130120116003) /IT/C-1
GANDHINAGAR INSTITUTE OF
TECHNOLOGY

3. INTRODUCTION:
 A matrix is a rectangular table of elements which may be
numbers or abstract quantities that can be added and
multiplied .
 Matrices are used to describe linear equations, record
data that depends on multiple parameters.
 There are many applications of matrices in maths viz.
graph theory, probality theory, statistics , computer
graphics, geometrical optics,etc

4.  Matrix:
 A set of mn elements arranged in a rectangular
array of m rows and n columns is called a matrix of
order m by n, written as m*n.

5. SOME DEFINITIONS ASSOCIATED WITH
MATRICES:
 Row matrix:
A matrix having only one row and any number of columns
eg:
 Column matrix:
A matrix having one column and any number of rows
eg:

6.  Zero or null matrix:
A matrix whose all the elements are zero is called zero matrix
eg:
 Diagonal matrix:
A square matrix all of whose non-diagonal elements are zero and at
least one diagonal elements is non-zero
eg:

7.  Unit or identity matrix:
A diagonal matrix all of whose diagonal elements are
unity is called a unit or identity matrix and is denoted by I
eg:
 Scalar matrix:
A diagonal matrix all of whose diagonal elements are
equal is called a scalar matrix
eg:

8.  Upper triangular matrix:
A square matrix in which all the elements below the diagonal are zero is called upper
triangular matrix
eg:
 Lower triangular matrix:
A square matrix in which all the elements above the diagonal are zero is called a lower
triangular matrix
eg:
 Trace of a matrix:
The sum of all diagonal elements of a square matrix
eg: trace of A =1+4+6+11
A =

9.  Transpose of a matrix:
a matrix obtained by interchanging rows and columns of a matrix is called
transpose of a matrix and is denoted by A’
eg:
 Determinant of a matrix:
if A is a square matrix then determinant of A is represented as IAI or det(A)
 Singular and non singular matrices:
a square matrix A is called singular if det(A) =0 and non-singular if det(A)≠0.

10. Some special matrices:
 Symmetric matrix:
A square matrix A that is equal to its transpose, i.e., A = AT or is
a symmetric matrix
 Skew symmetric matrix:
A was equal to the negative of its transpose, i.e., A =−AT, then A is
a skew symmetric matrix
eg:

11.  Conjugate of a matrix:
A matrix obtained from any given matrix A, on replacing its elements by
the corresponding conjugate complex numbers is called the conjugate of
A and is denoted by A
 Transposed conjugate of a matrix:
The conjugate of the transpose of a matrix A is called the transposed
conjugate or conjugate transpose of A and is denoted by

12.  Hermitian matrix:
A square matrix is called Hermitian if
eg:
 Skew Hermitian matrix:
A square matrix is called skew matrix if A = −A*
eg: if then

13.  Unitary matrix:
A square matrix is called unitary if AA*= A*A=I
 Orthogonal matrix:
A square matrix A is called orthogonal if AT A=AAT =I.