AB
Uploaded byAhmadreza Barazesh
PPTX, PDF11,996 views

Powder blending scaleup

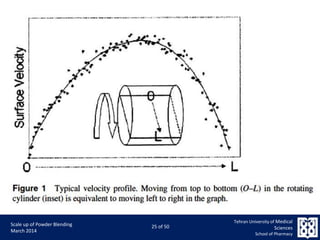
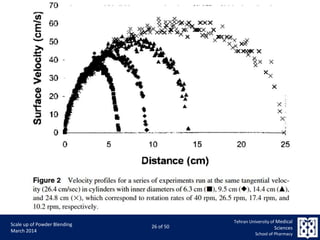
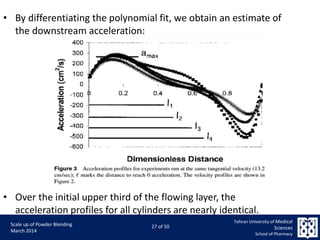
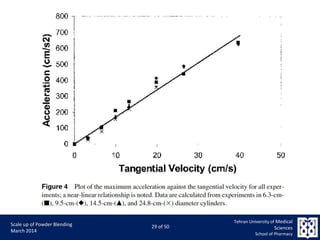
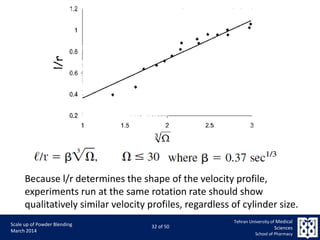
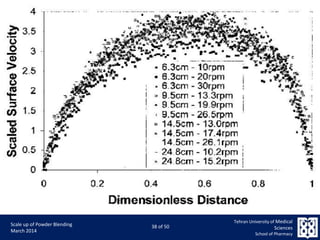
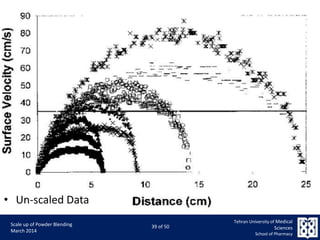
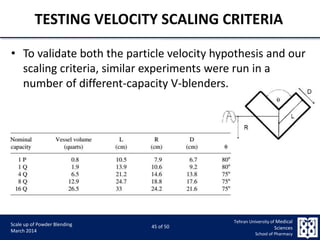
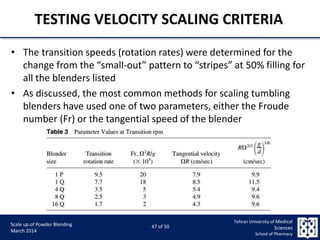
This document discusses the challenges and considerations in scaling up powder blending processes, particularly in tumbling blenders. It emphasizes the importance of achieving homogeneity and addresses various factors such as speed, load, and particle dynamics that influence blending effectiveness. The authors propose new models and scaling criteria to enhance understanding of mixture behavior during the scale-up of blending operations.

Embed presentation

Downloaded 310 times
9/5/2015 1 Scale up of Powder Blending March 2014 1 of 50 Tehran University of Medical Sciences School of Pharmacy Batch Size Increase in Dry Blending and Mixing Chapter by:Albert W. Alexander and Fernando J. Muzzio
9/5/2015 2 Scale up of Powder Blending March 2014 2 of 50 Tehran University of Medical Sciences School of Pharmacy Introduction • Dry particle blending is a critical step that has a direct impact on content uniformity • There are currently no mathematical techniques to predict blending behavior of granular components without prior experimental work. • Blending studies start with a small-scale, try-it- and-see approach.
9/5/2015 3 Scale up of Powder Blending March 2014 3 of 50 Tehran University of Medical Sciences School of Pharmacy A Typical Problem • A 5ft3 tumble blender filled to 50% of capacity and run at 15 rpm for 15 min produces the desired mixture homogeneity. What conditions should be used to duplicate these results in a 25ft3 blender? • The following questions might arise: – 1. What rotation rate should be used? – 2. Should filling level be the same? – 3. How long should the blender be operated? – 4. Are variations to the blender geometry between scales acceptable?
9/5/2015 4 Scale up of Powder Blending March 2014 4 of 50 Tehran University of Medical Sciences School of Pharmacy Tumbling Blenders
9/5/2015 5 Scale up of Powder Blending March 2014 5 of 50 Tehran University of Medical Sciences School of Pharmacy Defining Mixedness • The final objective of any granular mixing process is homogeneity. • No reliable techniques for on-line measuring of composition have been developed yet. • Granular mixtures are usually quantified by removing samples from the mixture. • Interrupting the blend cycle and repeated sampling may change the state of the blend. • The mean value and sample variance are determined and then often used in a mixing index.
9/5/2015 6 Scale up of Powder Blending March 2014 6 of 50 Tehran University of Medical Sciences School of Pharmacy Online Processing of Homogenicity • Imaging (NIR) • Image Processing
9/5/2015 7 Scale up of Powder Blending March 2014 7 of 50 Tehran University of Medical Sciences School of Pharmacy Mixing in Tumbling Blenders • Particle motions is in a thin, cascading layer at the surface, while the remainder of the material rotates with the vessel as a rigid body. • Most tumbling blenders are symmetrical which impedes achieving a homogeneous mixture. • The mixing rate often becomes limited by the amount of material that can cross from one side of the symmetry plane to the other
9/5/2015 8 Scale up of Powder Blending March 2014 8 of 50 Tehran University of Medical Sciences School of Pharmacy Mixing in Tumbling Blenders • Blending process takes place by three essentially independent mechanisms: • Convection causes large groups of particles to move in the direction of flow (orthogonal to the axis of rotation), the result of vessel rotation. • Dispersion is the random motion of particles as a result of collisions or inter-particle motion, usually orthogonal to the direction of flow (parallel to the axis of rotation). • Shear separates particles that have joined due to agglomeration or cohesion and requires high forces.
9/5/2015 9 Scale up of Powder Blending March 2014 9 of 50 Tehran University of Medical Sciences School of Pharmacy Mixing in Tumbling Blenders • Loading of multiple ingredients will have a dramatic effect on mixing rate if dispersion is the critical blending mechanism. • Care must be taken when loading a minor (~1%) component into the blender • The order of constituent addition can also have significant effects on the degree of final homogeneity, especially if ordered mixing (bonding of one component to another) can occur within the blend
9/5/2015 10 Scale up of Powder Blending March 2014 10 of 50 Tehran University of Medical Sciences School of Pharmacy Mixing in Tumbling Blenders • Intershell flow is the slowest step in a V-blender, because it is dispersive in nature, while intrashell flow is convective. Both processes can be described by similar mathematics, typically using an equation such as: • Where σ2 is mixture variance, N is the number of revolutions, A is an unspecified constant, and k is the rate constant. • The rate constants for convective mixing are orders of magnitude greater than for dispersive mixing.
9/5/2015 11 Scale up of Powder Blending March 2014 11 of 50 Tehran University of Medical Sciences School of Pharmacy Process Parameters • One parameter consideration that arises is whether rotation rate should change with variations in size. • When far from the critical speed of the blender, the rotation rate does not have strong effects on the mixing rate • The number of revolutions was the most important parameter governing the mixing rate.
9/5/2015 12 Scale up of Powder Blending March 2014 12 of 50 Tehran University of Medical Sciences School of Pharmacy Process Parameters • Given a geometrically similar blender and the same mixture composition, the fill level should also be kept constant with changes in scale. • However, an increase in vessel size at the same fill level may correspond to a significant decrease in the relative volume of particles in the cascading layer compared to the bulk. • A large decrease in mixing rate.
9/5/2015 13 Scale up of Powder Blending March 2014 13 of 50 Tehran University of Medical Sciences School of Pharmacy SCALE-UP APPROACHES • Froude number Fr=Ω2R/g Where Ω is the rotation rate, R is the vessel radius, and g is the acceleration from gravity is often suggested for tumbling blender scale-up. • Matching Tangential Speed A less commonly recommended scaling strategy is to match the tangential speed (wall speed) of the blender; however, this hypothesis also remains untested Whatisthe dimensionofFr?
9/5/2015 14 Scale up of Powder Blending March 2014 14 of 50 Tehran University of Medical Sciences School of Pharmacy Back to our problem with a Fr approach • We now look at our general problem of scaling the 5ft3 blender using Fr as the scaling approach: • The requisites are: – Geometric Similarity – Keep total number of revolutions constant
9/5/2015 15 Scale up of Powder Blending March 2014 15 of 50 Tehran University of Medical Sciences School of Pharmacy Back to our problem with a Fr approach • the 25ft3 blender must look like a photocopy enlargement of the 5ft3 blender. So the linear increase is 51/3, or 71%. • Also the fill level must remain the same. • To maintain the same Froude number, since R has increased by 71%, the rpm (Ω) must be reduced by a factor of (1.71)-1/2 = 0.76, corresponding to 11.5 rpm • The speed closest to 11.5 rpm would be selected.
9/5/2015 16 Scale up of Powder Blending March 2014 16 of 50 Tehran University of Medical Sciences School of Pharmacy Back to our problem with a Fr approach • If the initial blend time were 15 minutes at 15 rpm, the total revolutions of 225 must be maintained with the 25ft3 scale. Assuming 11.5 rpm were selected, this would amount to a 19.5- minute blend time.
9/5/2015 17 Scale up of Powder Blending March 2014 17 of 50 Tehran University of Medical Sciences School of Pharmacy NEW APPROACH TO THE SCALE-UP PROBLEM IN TUMBLING BLENDERS • We begin by proposing a set of variables that may control the process. • The driving force for flow in tumbling blenders is the acceleration from gravity. • Vessel size is obviously a critical parameter, as is the rotation rate, which defines the energy input to the system. • These variables define the system parameters but do not cover the mixture response.
9/5/2015 18 Scale up of Powder Blending March 2014 18 of 50 Tehran University of Medical Sciences School of Pharmacy NEW APPROACH TO THE SCALE-UP PROBLEM IN TUMBLING BLENDERS • In case of Newtonian fluids: Driving Forces (pressure gradients, gravity, shear) Fluid Response (velocity gradients) Viscosity • For granular mixtures: Driving Forces (gravity, vessel size ) Particle Size and Interactions Fluid Response (velocity gradients, blending rate)
9/5/2015 19 Scale up of Powder Blending March 2014 19 of 50 Tehran University of Medical Sciences School of Pharmacy NEW APPROACH TO THE SCALE-UP PROBLEM IN TUMBLING BLENDERS • For granular mixtures we will define particle size and particle velocity as our “performance variables.” • Particle size plays a large role in determining mixing (or segregation) rates because dispersion distance is expected to vary inversely with particle size.
9/5/2015 20 Scale up of Powder Blending March 2014 20 of 50 Tehran University of Medical Sciences School of Pharmacy NEW APPROACH TO THE SCALE-UP PROBLEM IN TUMBLING BLENDERS • Although previous studies have indicated that rotation rate (and, hence, probably particle velocities) does not affect mixing rate, these experiments were done in very small blenders. It is conceivable that at larger scales, these variables could become important. • We can now address the development of non- dimensional scaling criteria.
9/5/2015 21 Scale up of Powder Blending March 2014 21 of 50 Tehran University of Medical Sciences School of Pharmacy Applying Rayleigh’s Method • Variables that are believed to govern particle dynamics in tumbling blenders are listed: • Using these variables and the Rayleigh method, we derive the following equation: Lord Rayleigh’s sarcastic comment with which he began his short essay on “The Principle of Similitude” “I have often been impressed by the scanty attention paid even by original workers in physics to the great principle of similitude. It happens not infrequently that results in the form of ‘laws’ are put forward as novelties on the basis of elaborate experiments, which might have been predicted a priori after a few minutes’ consideration.”
9/5/2015 22 Scale up of Powder Blending March 2014 22 of 50 Tehran University of Medical Sciences School of Pharmacy Dimensional Homogenization • Applying the rule of dimensional homogeneity and making c and e the unrestricted constants leads to:
9/5/2015 23 Scale up of Powder Blending March 2014 23 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • In order to determine particle velocities, an empirical approach is taken. • A digital video camera was used to record the positions of individual particles on the flowing surface in clear acrylic, rotating cylinders of 6.3, 9.5, 14.5, and 24.8cm diameter filled to 50% of capacity. • nearly monodisperse 1.6mm glass beads dyed for visualization was used.
9/5/2015 24 Scale up of Powder Blending March 2014 24 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • The displacement of particles from one frame to the next was converted into velocities. • To calculate velocity, only the motion down the flowing layer was used, and all cross-stream (i.e., dispersive) motion was ignored.
9/5/2015 25 Scale up of Powder Blending March 2014 25 of 50 Tehran University of Medical Sciences School of Pharmacy
9/5/2015 26 Scale up of Powder Blending March 2014 26 of 50 Tehran University of Medical Sciences School of Pharmacy
9/5/2015 27 Scale up of Powder Blending March 2014 27 of 50 Tehran University of Medical Sciences School of Pharmacy • By differentiating the polynomial fit, we obtain an estimate of the downstream acceleration: • Over the initial upper third of the flowing layer, the acceleration profiles for all cylinders are nearly identical.
9/5/2015 28 Scale up of Powder Blending March 2014 28 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • maximum accelerations are nearly equal, implying that tangential velocity may be proportional to maximum acceleration. • Maximum accelerations were determined for all experiments; the results are plotted against the tangential velocity
9/5/2015 29 Scale up of Powder Blending March 2014 29 of 50 Tehran University of Medical Sciences School of Pharmacy
9/5/2015 30 Scale up of Powder Blending March 2014 30 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • An Approximate Linear fit: • where TV is the tangential velocity (=2πRΩ) and α = 17 sec-1, is seen relating acceleration and tangential velocity for all cylinders and rotation rates.
9/5/2015 31 Scale up of Powder Blending March 2014 31 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • The distance to reach zero acceleration, l, by itself, has little meaning but the parameter l/r, where r is the cylinder radius, that has a quantitative effect on the velocity profile and maximum velocities. • When all values of l/r were compiled, a strong correlation to rotation rate was noted.
9/5/2015 32 Scale up of Powder Blending March 2014 32 of 50 Tehran University of Medical Sciences School of Pharmacy Because l/r determines the shape of the velocity profile, experiments run at the same rotation rate should show qualitatively similar velocity profiles, regardless of cylinder size.
9/5/2015 33 Scale up of Powder Blending March 2014 33 of 50 Tehran University of Medical Sciences School of Pharmacy Developing a Model • The simplest possible model for particle velocity relates velocity and distance when acceleration is constant, • Where V0 is the initial downstream velocity and x is the downstream coordinate.
9/5/2015 34 Scale up of Powder Blending March 2014 34 of 50 Tehran University of Medical Sciences School of Pharmacy • Some simplifying assumptions: 1. Particles emerge into the flowing layer with zero initial downstream velocity V0= 0 2. Peak acceleration is proportional to the tangential velocity (TV), 3. Particles accelerate over the distance l. 4. Acceleration (a) is not constant over the distance l, but the rate of change in acceleration scales appropriately with the value of l (i.e., a = amaxƒ(x/l), where x is the distance down the cascade). Developing a Model
9/5/2015 35 Scale up of Powder Blending March 2014 35 of 50 Tehran University of Medical Sciences School of Pharmacy Developing a Model • Using these assumptions a new relation for particle velocity would be: • Which relates particle velocities to the rotation rate and the radius, can be used as the basis for scaling particle velocities with changes in cylinder diameter and rotation rate.
9/5/2015 36 Scale up of Powder Blending March 2014 36 of 50 Tehran University of Medical Sciences School of Pharmacy Returning to Dimensional Analysis • This equation can be used to complete the dimensional analysis discussed earlier. • Applying dimensional homogeneity and solving leads to:
9/5/2015 37 Scale up of Powder Blending March 2014 37 of 50 Tehran University of Medical Sciences School of Pharmacy Testing the Model • To test the scaling criteria suggested by equation we will look at velocity profiles between 10 and 30 rpm. Figure shows the scaled velocity profiles (i.e., all data are divided by using RΩ2/3(g/d)1/6, and the distance down the cascade is divided by the cylinder diameter
9/5/2015 38 Scale up of Powder Blending March 2014 38 of 50 Tehran University of Medical Sciences School of Pharmacy
9/5/2015 39 Scale up of Powder Blending March 2014 39 of 50 Tehran University of Medical Sciences School of Pharmacy • Un-scaled Data
9/5/2015 40 Scale up of Powder Blending March 2014 40 of 50 Tehran University of Medical Sciences School of Pharmacy Returning to our example • scaling from a 5-ft3 blender to a 25-ft 3 blender, again the relative change in length is 71%. This time, to scale surface velocities using this approach, the blending speed (Ω) must be reduced by a factor of (1.71)-3/2 = 0.45, corresponding to 6.7 rpm (assuming the particle diameter, d,remains constant). • Again, the total number of revolutions would remain constant at 225, for a blend time of 33.6 min.
9/5/2015 41 Scale up of Powder Blending March 2014 41 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • Experimental work has not validated the preceding scaling procedure with respect to scale-up of blending processes. • This model should not be favored over other approaches currently in use, though it may provide additional insight.
9/5/2015 42 Scale up of Powder Blending March 2014 42 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • recent work has indicated that particle velocities may be critical for determining segregation dynamics in double-cone blenders and V- blenders. • Segregation occurs within the blender as particles begin to flow in regular, defined patterns that differ according to their particle size.
9/5/2015 43 Scale up of Powder Blending March 2014 43 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • In a 1.9-quart-capacity V-blender at fixed filling (50%), incrementally changing rotation rate induced a transition between two segregation patterns • At the lower rotation rate, the “small-out” pattern forms • At a slightly higher rotation rate, the “stripes” pattern forms
9/5/2015 44 Scale up of Powder Blending March 2014 44 of 50 Tehran University of Medical Sciences School of Pharmacy Segregation Patterns
9/5/2015 45 Scale up of Powder Blending March 2014 45 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • To validate both the particle velocity hypothesis and our scaling criteria, similar experiments were run in a number of different-capacity V-blenders.
9/5/2015 46 Scale up of Powder Blending March 2014 46 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • All the vessels are constructed from clear plexiglass, enabling visual identification of segregation patterns. • For these experiments, a binary mixture of sieved fractions of 150 to 250-(nominally 200) and 710- to 840- (nominally 775-) glass beads was used. • A symmetrical initial condition (top-to-bottom loading) is implemented. • The blender is run at constant rotation rate; a segregation pattern was assumed to be stable when it did not discernibly change for 100 revolutions.
9/5/2015 47 Scale up of Powder Blending March 2014 47 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • The transition speeds (rotation rates) were determined for the change from the “small-out” pattern to “stripes” at 50% filling for all the blenders listed • As discussed, the most common methods for scaling tumbling blenders have used one of two parameters, either the Froude number (Fr) or the tangential speed of the blender
9/5/2015 48 Scale up of Powder Blending March 2014 48 of 50 Tehran University of Medical Sciences School of Pharmacy RECOMMENDATIONS AND CONCLUSIONS • The analysis of particle velocities provides a good first step toward the rigorous development of scaling criteria for granular flow, but it is far from conclusive. • It is important in granular systems to first determine the dynamic variable that governs the process at hand before determining scaling rules • A systematic, generalized approach for the scale-up of granular mixing devices is still far from attainable. Clearly, more research is required both to test current hypotheses and to generate new approaches to the problem.
9/5/2015 49 Scale up of Powder Blending March 2014 49 of 50 Tehran University of Medical Sciences School of Pharmacy some simple guidelines that can help through the scale-up Make sure that changes in scale have not changed the dominant mixing mechanism in the blender (i.e., convective to dispersive) Number of revolutions is a key parameter, but rotation rates are largely unimportant. When performing scale-up tests, be sure to take enough samples, be wary of how you interpret your samples. One simple way to increase mixing rate is to decrease the fill level. It also reduces the probability that dead zones will form. Addition of asymmetry into the vessel, either by design or baffles, can have a tremendous impact on mixing rate.

More Related Content

PPSX
HSMG RMG High Shear Mixer Granulator
byGautam Saurabh
 
PDF
Fbd(Fluidized Bed Dryer)
byNandhini Podamekala
 
PPTX
Parenteral Production process sterilisation and filling
byAffrin Shaik
 
PPT
GMP Requirements for Sterile Products manufacturing
bysurafel kebede
 
PPTX
Pilot plantscaleupof parentrals
byMalla Reddy College of Pharmacy
 
PDF
Milling Pharmaceutical Industry
byDr Ahmad Abdulhusiaan Yosef
 
PPTX
Pelletization and granulation
byUsman Shah
 
PPTX
cGMP's for sterile products
byGMP EDUCATION : Not for Profit Organization
 
HSMG RMG High Shear Mixer Granulator
byGautam Saurabh
 
Fbd(Fluidized Bed Dryer)
byNandhini Podamekala
 
Parenteral Production process sterilisation and filling
byAffrin Shaik
 
GMP Requirements for Sterile Products manufacturing
bysurafel kebede
 
Pilot plantscaleupof parentrals
byMalla Reddy College of Pharmacy
 
Milling Pharmaceutical Industry
byDr Ahmad Abdulhusiaan Yosef
 
Pelletization and granulation
byUsman Shah
 
cGMP's for sterile products
byGMP EDUCATION : Not for Profit Organization
 

What's hot

PDF
Drug excipient Compatibility
bySuraj Choudhary
 
PPT
Blending
byNiket Patel
 
PPTX
Dissolution - Selection of Dissolution Media
bySagar K Savale
 
PPTX
solubility and solubilization
bysindhu kondaveti
 
PPTX
selection of dissolution medium And dissolution study of solid dosage form
byAshwin Patil
 
PPT
Rapid mixer granulator
byRavish Yadav
 
PPTX
DISSOLUTION AND FACTORS AFFECTING DISSOLUTION
byDiksha Tapsale
 
PPTX
Parenteral production
byceutics1315
 
PPTX
Solid state drug stability
byAnindya Jana
 
PPTX
Powder flow testing and control
byNitin Patel
 
PPTX
Size saperation introduction
bybvocmithilesh
 
PPTX
Coating technology
byPRANJAY PATIL
 
PDF
Validation of liquids
byPriyam Patel
 
PPT
validation of homogenizer.ppt
byshivakumarRavula1
 
PPTX
ACCELERATED STABILITY STUDY
byPratikkumarjain
 
DOC
Equipment validation of tablet compression ( machine)
byMalla Reddy College of Pharmacy
 
PPTX
Solubility & Method for determination of solubility
byZulcaif Ahmad
 
PPTX
HECKEL PLOT CEUTICS .pptx
byAbdulNaim14
 
PPTX
Pre formulation protocol
byAmruta Balekundri
 
PPTX
Qualification of Tray Dryer.pptx
byDhruvi50
 
Drug excipient Compatibility
bySuraj Choudhary
 
Blending
byNiket Patel
 
Dissolution - Selection of Dissolution Media
bySagar K Savale
 
solubility and solubilization
bysindhu kondaveti
 
selection of dissolution medium And dissolution study of solid dosage form
byAshwin Patil
 
Rapid mixer granulator
byRavish Yadav
 
DISSOLUTION AND FACTORS AFFECTING DISSOLUTION
byDiksha Tapsale
 
Parenteral production
byceutics1315
 
Solid state drug stability
byAnindya Jana
 
Powder flow testing and control
byNitin Patel
 
Size saperation introduction
bybvocmithilesh
 
Coating technology
byPRANJAY PATIL
 
Validation of liquids
byPriyam Patel
 
validation of homogenizer.ppt
byshivakumarRavula1
 
ACCELERATED STABILITY STUDY
byPratikkumarjain
 
Equipment validation of tablet compression ( machine)
byMalla Reddy College of Pharmacy
 
Solubility & Method for determination of solubility
byZulcaif Ahmad
 
HECKEL PLOT CEUTICS .pptx
byAbdulNaim14
 
Pre formulation protocol
byAmruta Balekundri
 
Qualification of Tray Dryer.pptx
byDhruvi50
 

Viewers also liked

PPT
CS 354 Blending, Compositing, Anti-aliasing
byMark Kilgard
 
PPT
Powders
byKiran Hameed
 
PPT
Mixing of liquids, solids and high viscosity materials
byUniquemixers & Furnaces Pvt. Ltd.
 
PPT
Analytical Techniques In Determining On Line Blend Uniformity In Powder Techn...
byDebanjan (Deb) Das
 
PPT
Separation mechanism
byRabiul Hasan
 
PPTX
Pilot plant scale up techniques for solid dosage forms
byElahehEntezarmahdi
 
PPTX
Scale up report presentation
bySherry Coutu CBE
 
PPTX
Powders
byKARTHIKA K.J
 
PPTX
Liquid mixing
bykhehkesha
 
PPT
introduction to blender
byanand09
 
PPS
Mixing and stirring
byjoostjansma
 
DOCX
[Paperwork] Mixing - Pharmaceutical Engineering
byAnnisa Hayatunnufus
 
PPT
Separation of Mixtures
byJacklyn Kong
 
PPTX
[Power Point] Mixing - Pharmaceutical Engineering
byAnnisa Hayatunnufus
 
PPT
Pilot plant scale up techniques
bySujit Patel
 
PPT
Agitation and mixing
byIhsan Ali
 
DOC
Occupancy calculation form
byFrankie Jones
 
PPT
Powder metallurgy
byShailendra Pratap Singh
 
PPTX
NOVEL SEPARATION AND QUANTITATIVE DETERMINATION OF LEVOFLOXACIN, PRULIFLOXACI...
byDr. Ravi Sankar
 
PPTX
Mixing and homogenization
byNabiilah Naraino Majie
 
CS 354 Blending, Compositing, Anti-aliasing
byMark Kilgard
 
Powders
byKiran Hameed
 
Mixing of liquids, solids and high viscosity materials
byUniquemixers & Furnaces Pvt. Ltd.
 
Analytical Techniques In Determining On Line Blend Uniformity In Powder Techn...
byDebanjan (Deb) Das
 
Separation mechanism
byRabiul Hasan
 
Pilot plant scale up techniques for solid dosage forms
byElahehEntezarmahdi
 
Scale up report presentation
bySherry Coutu CBE
 
Powders
byKARTHIKA K.J
 
Liquid mixing
bykhehkesha
 
introduction to blender
byanand09
 
Mixing and stirring
byjoostjansma
 
[Paperwork] Mixing - Pharmaceutical Engineering
byAnnisa Hayatunnufus
 
Separation of Mixtures
byJacklyn Kong
 
[Power Point] Mixing - Pharmaceutical Engineering
byAnnisa Hayatunnufus
 
Pilot plant scale up techniques
bySujit Patel
 
Agitation and mixing
byIhsan Ali
 
Occupancy calculation form
byFrankie Jones
 
Powder metallurgy
byShailendra Pratap Singh
 
NOVEL SEPARATION AND QUANTITATIVE DETERMINATION OF LEVOFLOXACIN, PRULIFLOXACI...
byDr. Ravi Sankar
 
Mixing and homogenization
byNabiilah Naraino Majie
 

Similar to Powder blending scaleup

PDF
mixing final (1).pdf
byAnandPandey888127
 
PPTX
Mixing.pptx
bySupriya Bhamare
 
PDF
mixing.pdf
byRAJARAVIHiCETAGRIFAC
 
PDF
MIXING.pdf
bysonuvarma1027
 
PPTX
Pilot Plant Techniques for SOLID dosage forms
byD.R. Chandravanshi
 
PPTX
mixing-..pptx pharmaceutical engineering
byAdwaitSinkar
 
PPTX
mixing resentation by vidhi modh.pptx
byVidhiModi13
 
PDF
mixingbyankitayagnik-180430073509.pdf
bysafuraqazi
 
PPTX
Mixing by ankita yagnik
byAnkita Yagnik
 
PDF
mixing final (1) (1).pdf
byAnandPandey888127
 
PPTX
B-pharm-Pilot plant technique-tablets^.pptx
byDibenthiranS
 
PPTX
15mph104 dishant scale up
byDishant shah
 
PPTX
Pharmaceutical mixing and its importance
byRekhaU2
 
PPTX
Pharmaceutical Engineering (sem-3) unit 3-2
bypayalpilaji
 
PPTX
Pilot plant scale up for tablets
byRobin Gulati
 
PPTX
Mixers and different mixers in food industry
byAbel Jacob Thomas
 
PPTX
Mixing by robin paudel our dream safari.pptx
byRobinPaudel3
 
PDF
pilotplantdesignfortabletsandcapsules-140930004246-phpapp01 (1).pdf
byVaibhavwagh48
 
PPTX
Tablets
byYamini Shah
 
PPTX
Mixing part 3
byHussein Alkufi
 
mixing final (1).pdf
byAnandPandey888127
 
Mixing.pptx
bySupriya Bhamare
 
mixing.pdf
byRAJARAVIHiCETAGRIFAC
 
MIXING.pdf
bysonuvarma1027
 
Pilot Plant Techniques for SOLID dosage forms
byD.R. Chandravanshi
 
mixing-..pptx pharmaceutical engineering
byAdwaitSinkar
 
mixing resentation by vidhi modh.pptx
byVidhiModi13
 
mixingbyankitayagnik-180430073509.pdf
bysafuraqazi
 
Mixing by ankita yagnik
byAnkita Yagnik
 
mixing final (1) (1).pdf
byAnandPandey888127
 
B-pharm-Pilot plant technique-tablets^.pptx
byDibenthiranS
 
15mph104 dishant scale up
byDishant shah
 
Pharmaceutical mixing and its importance
byRekhaU2
 
Pharmaceutical Engineering (sem-3) unit 3-2
bypayalpilaji
 
Pilot plant scale up for tablets
byRobin Gulati
 
Mixers and different mixers in food industry
byAbel Jacob Thomas
 
Mixing by robin paudel our dream safari.pptx
byRobinPaudel3
 
pilotplantdesignfortabletsandcapsules-140930004246-phpapp01 (1).pdf
byVaibhavwagh48
 
Tablets
byYamini Shah
 
Mixing part 3
byHussein Alkufi
 

Recently uploaded

PPTX
DIFFERENT TYPES OF SRTUCTURAL SYSTEM ANALYSIS
bynoshin231202
 
PPTX
INTEGRATED COMMUNICATION AND SENSING Presentation.pptx
byNanaAgyeman13
 
PPTX
How Does LNG Regasification Work | INOXCVA
byINOXCVA
 
PDF
MoD_2.pptx solid rockets of the rocket.pdf
byrajaashish82988
 
PDF
Industrial Tools Manufacturers In India : Torso Tools
bytorsotools8
 
PDF
Plasticity and Structure of Soil/Atterberg Limits.pdf
byMahmoodKhalid11
 
PPTX
The Hidden Cost of Bad Spare Parts Planning (And How AI CMMS Fixes It)
byMaintWiz Technologies Private Limited
 
PPTX
ME3592 - Metrology and Measurements - Unit - 1 - Lecture Notes
bypprakash21252
 
PDF
Weak Incentives (WINK): The Agent Definition Layer
byAndrei Savu
 
PDF
(en/zhTW) Heterogeneous System Architecture: Design & Performance
byDanny Jiang
 
PPTX
Why Most SAP PM Implementations Fail — And How High-Reliability Plants Fix It
byMaintWiz Technologies Private Limited
 
PDF
Enhancing optical fiber communication systems using repetition coding for imp...
byMouweffeqBouregaa
 
PPTX
Why TPM Succeeds in Some Plants and Struggles in Others | MaintWiz
byMaintWiz Technologies Private Limited
 
PDF
Basics of Electronics Task by Vivaan Jo Varghese.pdf
byVivaan Jo Varghese
 
PPTX
traffic safety section seven (Traffic Control and Management) of Act
byazeRakeshSunariMagar
 
PPTX
Fuel Injection Pump Test Bench – Precision Testing & Calibration for Diesel E...
byNeometrix_Engineering_Pvt_Ltd
 
PDF
PROBLEM SLOVING AND PYTHON PROGRAMMING UNIT 3.pdf
byA R SIVANESH M.E., QIP-PG (Cyber Security)., (Ph.D)
 
PPTX
A professional presentation on Cosmos Bank Heist
byssuser7f0075
 
PPTX
Optimizing the ELBO Objective: A Comparative Study of RNN, LSTM, and GRU Arch...
byKayalvizhi A
 
PDF
Highway Curves in Transportation Engineering.pdf
byMahmoodKhalid11
 
DIFFERENT TYPES OF SRTUCTURAL SYSTEM ANALYSIS
bynoshin231202
 
INTEGRATED COMMUNICATION AND SENSING Presentation.pptx
byNanaAgyeman13
 
How Does LNG Regasification Work | INOXCVA
byINOXCVA
 
MoD_2.pptx solid rockets of the rocket.pdf
byrajaashish82988
 
Industrial Tools Manufacturers In India : Torso Tools
bytorsotools8
 
Plasticity and Structure of Soil/Atterberg Limits.pdf
byMahmoodKhalid11
 
The Hidden Cost of Bad Spare Parts Planning (And How AI CMMS Fixes It)
byMaintWiz Technologies Private Limited
 
ME3592 - Metrology and Measurements - Unit - 1 - Lecture Notes
bypprakash21252
 
Weak Incentives (WINK): The Agent Definition Layer
byAndrei Savu
 
(en/zhTW) Heterogeneous System Architecture: Design & Performance
byDanny Jiang
 
Why Most SAP PM Implementations Fail — And How High-Reliability Plants Fix It
byMaintWiz Technologies Private Limited
 
Enhancing optical fiber communication systems using repetition coding for imp...
byMouweffeqBouregaa
 
Why TPM Succeeds in Some Plants and Struggles in Others | MaintWiz
byMaintWiz Technologies Private Limited
 
Basics of Electronics Task by Vivaan Jo Varghese.pdf
byVivaan Jo Varghese
 
traffic safety section seven (Traffic Control and Management) of Act
byazeRakeshSunariMagar
 
Fuel Injection Pump Test Bench – Precision Testing & Calibration for Diesel E...
byNeometrix_Engineering_Pvt_Ltd
 
PROBLEM SLOVING AND PYTHON PROGRAMMING UNIT 3.pdf
byA R SIVANESH M.E., QIP-PG (Cyber Security)., (Ph.D)
 
A professional presentation on Cosmos Bank Heist
byssuser7f0075
 
Optimizing the ELBO Objective: A Comparative Study of RNN, LSTM, and GRU Arch...
byKayalvizhi A
 
Highway Curves in Transportation Engineering.pdf
byMahmoodKhalid11
 

Powder blending scaleup

  • 1.
    9/5/2015 1 Scale upof Powder Blending March 2014 1 of 50 Tehran University of Medical Sciences School of Pharmacy Batch Size Increase in Dry Blending and Mixing Chapter by:Albert W. Alexander and Fernando J. Muzzio
  • 2.
    9/5/2015 2 Scale upof Powder Blending March 2014 2 of 50 Tehran University of Medical Sciences School of Pharmacy Introduction • Dry particle blending is a critical step that has a direct impact on content uniformity • There are currently no mathematical techniques to predict blending behavior of granular components without prior experimental work. • Blending studies start with a small-scale, try-it- and-see approach.
  • 3.
    9/5/2015 3 Scale upof Powder Blending March 2014 3 of 50 Tehran University of Medical Sciences School of Pharmacy A Typical Problem • A 5ft3 tumble blender filled to 50% of capacity and run at 15 rpm for 15 min produces the desired mixture homogeneity. What conditions should be used to duplicate these results in a 25ft3 blender? • The following questions might arise: – 1. What rotation rate should be used? – 2. Should filling level be the same? – 3. How long should the blender be operated? – 4. Are variations to the blender geometry between scales acceptable?
  • 4.
    9/5/2015 4 Scale upof Powder Blending March 2014 4 of 50 Tehran University of Medical Sciences School of Pharmacy Tumbling Blenders
  • 5.
    9/5/2015 5 Scale upof Powder Blending March 2014 5 of 50 Tehran University of Medical Sciences School of Pharmacy Defining Mixedness • The final objective of any granular mixing process is homogeneity. • No reliable techniques for on-line measuring of composition have been developed yet. • Granular mixtures are usually quantified by removing samples from the mixture. • Interrupting the blend cycle and repeated sampling may change the state of the blend. • The mean value and sample variance are determined and then often used in a mixing index.
  • 6.
    9/5/2015 6 Scale upof Powder Blending March 2014 6 of 50 Tehran University of Medical Sciences School of Pharmacy Online Processing of Homogenicity • Imaging (NIR) • Image Processing
  • 7.
    9/5/2015 7 Scale upof Powder Blending March 2014 7 of 50 Tehran University of Medical Sciences School of Pharmacy Mixing in Tumbling Blenders • Particle motions is in a thin, cascading layer at the surface, while the remainder of the material rotates with the vessel as a rigid body. • Most tumbling blenders are symmetrical which impedes achieving a homogeneous mixture. • The mixing rate often becomes limited by the amount of material that can cross from one side of the symmetry plane to the other
  • 8.
    9/5/2015 8 Scale upof Powder Blending March 2014 8 of 50 Tehran University of Medical Sciences School of Pharmacy Mixing in Tumbling Blenders • Blending process takes place by three essentially independent mechanisms: • Convection causes large groups of particles to move in the direction of flow (orthogonal to the axis of rotation), the result of vessel rotation. • Dispersion is the random motion of particles as a result of collisions or inter-particle motion, usually orthogonal to the direction of flow (parallel to the axis of rotation). • Shear separates particles that have joined due to agglomeration or cohesion and requires high forces.
  • 9.
    9/5/2015 9 Scale upof Powder Blending March 2014 9 of 50 Tehran University of Medical Sciences School of Pharmacy Mixing in Tumbling Blenders • Loading of multiple ingredients will have a dramatic effect on mixing rate if dispersion is the critical blending mechanism. • Care must be taken when loading a minor (~1%) component into the blender • The order of constituent addition can also have significant effects on the degree of final homogeneity, especially if ordered mixing (bonding of one component to another) can occur within the blend
  • 10.
    9/5/2015 10 Scale upof Powder Blending March 2014 10 of 50 Tehran University of Medical Sciences School of Pharmacy Mixing in Tumbling Blenders • Intershell flow is the slowest step in a V-blender, because it is dispersive in nature, while intrashell flow is convective. Both processes can be described by similar mathematics, typically using an equation such as: • Where σ2 is mixture variance, N is the number of revolutions, A is an unspecified constant, and k is the rate constant. • The rate constants for convective mixing are orders of magnitude greater than for dispersive mixing.
  • 11.
    9/5/2015 11 Scale upof Powder Blending March 2014 11 of 50 Tehran University of Medical Sciences School of Pharmacy Process Parameters • One parameter consideration that arises is whether rotation rate should change with variations in size. • When far from the critical speed of the blender, the rotation rate does not have strong effects on the mixing rate • The number of revolutions was the most important parameter governing the mixing rate.
  • 12.
    9/5/2015 12 Scale upof Powder Blending March 2014 12 of 50 Tehran University of Medical Sciences School of Pharmacy Process Parameters • Given a geometrically similar blender and the same mixture composition, the fill level should also be kept constant with changes in scale. • However, an increase in vessel size at the same fill level may correspond to a significant decrease in the relative volume of particles in the cascading layer compared to the bulk. • A large decrease in mixing rate.
  • 13.
    9/5/2015 13 Scale upof Powder Blending March 2014 13 of 50 Tehran University of Medical Sciences School of Pharmacy SCALE-UP APPROACHES • Froude number Fr=Ω2R/g Where Ω is the rotation rate, R is the vessel radius, and g is the acceleration from gravity is often suggested for tumbling blender scale-up. • Matching Tangential Speed A less commonly recommended scaling strategy is to match the tangential speed (wall speed) of the blender; however, this hypothesis also remains untested Whatisthe dimensionofFr?
  • 14.
    9/5/2015 14 Scale upof Powder Blending March 2014 14 of 50 Tehran University of Medical Sciences School of Pharmacy Back to our problem with a Fr approach • We now look at our general problem of scaling the 5ft3 blender using Fr as the scaling approach: • The requisites are: – Geometric Similarity – Keep total number of revolutions constant
  • 15.
    9/5/2015 15 Scale upof Powder Blending March 2014 15 of 50 Tehran University of Medical Sciences School of Pharmacy Back to our problem with a Fr approach • the 25ft3 blender must look like a photocopy enlargement of the 5ft3 blender. So the linear increase is 51/3, or 71%. • Also the fill level must remain the same. • To maintain the same Froude number, since R has increased by 71%, the rpm (Ω) must be reduced by a factor of (1.71)-1/2 = 0.76, corresponding to 11.5 rpm • The speed closest to 11.5 rpm would be selected.
  • 16.
    9/5/2015 16 Scale upof Powder Blending March 2014 16 of 50 Tehran University of Medical Sciences School of Pharmacy Back to our problem with a Fr approach • If the initial blend time were 15 minutes at 15 rpm, the total revolutions of 225 must be maintained with the 25ft3 scale. Assuming 11.5 rpm were selected, this would amount to a 19.5- minute blend time.
  • 17.
    9/5/2015 17 Scale upof Powder Blending March 2014 17 of 50 Tehran University of Medical Sciences School of Pharmacy NEW APPROACH TO THE SCALE-UP PROBLEM IN TUMBLING BLENDERS • We begin by proposing a set of variables that may control the process. • The driving force for flow in tumbling blenders is the acceleration from gravity. • Vessel size is obviously a critical parameter, as is the rotation rate, which defines the energy input to the system. • These variables define the system parameters but do not cover the mixture response.
  • 18.
    9/5/2015 18 Scale upof Powder Blending March 2014 18 of 50 Tehran University of Medical Sciences School of Pharmacy NEW APPROACH TO THE SCALE-UP PROBLEM IN TUMBLING BLENDERS • In case of Newtonian fluids: Driving Forces (pressure gradients, gravity, shear) Fluid Response (velocity gradients) Viscosity • For granular mixtures: Driving Forces (gravity, vessel size ) Particle Size and Interactions Fluid Response (velocity gradients, blending rate)
  • 19.
    9/5/2015 19 Scale upof Powder Blending March 2014 19 of 50 Tehran University of Medical Sciences School of Pharmacy NEW APPROACH TO THE SCALE-UP PROBLEM IN TUMBLING BLENDERS • For granular mixtures we will define particle size and particle velocity as our “performance variables.” • Particle size plays a large role in determining mixing (or segregation) rates because dispersion distance is expected to vary inversely with particle size.
  • 20.
    9/5/2015 20 Scale upof Powder Blending March 2014 20 of 50 Tehran University of Medical Sciences School of Pharmacy NEW APPROACH TO THE SCALE-UP PROBLEM IN TUMBLING BLENDERS • Although previous studies have indicated that rotation rate (and, hence, probably particle velocities) does not affect mixing rate, these experiments were done in very small blenders. It is conceivable that at larger scales, these variables could become important. • We can now address the development of non- dimensional scaling criteria.
  • 21.
    9/5/2015 21 Scale upof Powder Blending March 2014 21 of 50 Tehran University of Medical Sciences School of Pharmacy Applying Rayleigh’s Method • Variables that are believed to govern particle dynamics in tumbling blenders are listed: • Using these variables and the Rayleigh method, we derive the following equation: Lord Rayleigh’s sarcastic comment with which he began his short essay on “The Principle of Similitude” “I have often been impressed by the scanty attention paid even by original workers in physics to the great principle of similitude. It happens not infrequently that results in the form of ‘laws’ are put forward as novelties on the basis of elaborate experiments, which might have been predicted a priori after a few minutes’ consideration.”
  • 22.
    9/5/2015 22 Scale upof Powder Blending March 2014 22 of 50 Tehran University of Medical Sciences School of Pharmacy Dimensional Homogenization • Applying the rule of dimensional homogeneity and making c and e the unrestricted constants leads to:
  • 23.
    9/5/2015 23 Scale upof Powder Blending March 2014 23 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • In order to determine particle velocities, an empirical approach is taken. • A digital video camera was used to record the positions of individual particles on the flowing surface in clear acrylic, rotating cylinders of 6.3, 9.5, 14.5, and 24.8cm diameter filled to 50% of capacity. • nearly monodisperse 1.6mm glass beads dyed for visualization was used.
  • 24.
    9/5/2015 24 Scale upof Powder Blending March 2014 24 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • The displacement of particles from one frame to the next was converted into velocities. • To calculate velocity, only the motion down the flowing layer was used, and all cross-stream (i.e., dispersive) motion was ignored.
  • 25.
    9/5/2015 25 Scale upof Powder Blending March 2014 25 of 50 Tehran University of Medical Sciences School of Pharmacy
  • 26.
    9/5/2015 26 Scale upof Powder Blending March 2014 26 of 50 Tehran University of Medical Sciences School of Pharmacy
  • 27.
    9/5/2015 27 Scale upof Powder Blending March 2014 27 of 50 Tehran University of Medical Sciences School of Pharmacy • By differentiating the polynomial fit, we obtain an estimate of the downstream acceleration: • Over the initial upper third of the flowing layer, the acceleration profiles for all cylinders are nearly identical.
  • 28.
    9/5/2015 28 Scale upof Powder Blending March 2014 28 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • maximum accelerations are nearly equal, implying that tangential velocity may be proportional to maximum acceleration. • Maximum accelerations were determined for all experiments; the results are plotted against the tangential velocity
  • 29.
    9/5/2015 29 Scale upof Powder Blending March 2014 29 of 50 Tehran University of Medical Sciences School of Pharmacy
  • 30.
    9/5/2015 30 Scale upof Powder Blending March 2014 30 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • An Approximate Linear fit: • where TV is the tangential velocity (=2πRΩ) and α = 17 sec-1, is seen relating acceleration and tangential velocity for all cylinders and rotation rates.
  • 31.
    9/5/2015 31 Scale upof Powder Blending March 2014 31 of 50 Tehran University of Medical Sciences School of Pharmacy Correlating Particle Velocities to Vessel Rotation Rate and Radius • The distance to reach zero acceleration, l, by itself, has little meaning but the parameter l/r, where r is the cylinder radius, that has a quantitative effect on the velocity profile and maximum velocities. • When all values of l/r were compiled, a strong correlation to rotation rate was noted.
  • 32.
    9/5/2015 32 Scale upof Powder Blending March 2014 32 of 50 Tehran University of Medical Sciences School of Pharmacy Because l/r determines the shape of the velocity profile, experiments run at the same rotation rate should show qualitatively similar velocity profiles, regardless of cylinder size.
  • 33.
    9/5/2015 33 Scale upof Powder Blending March 2014 33 of 50 Tehran University of Medical Sciences School of Pharmacy Developing a Model • The simplest possible model for particle velocity relates velocity and distance when acceleration is constant, • Where V0 is the initial downstream velocity and x is the downstream coordinate.
  • 34.
    9/5/2015 34 Scale upof Powder Blending March 2014 34 of 50 Tehran University of Medical Sciences School of Pharmacy • Some simplifying assumptions: 1. Particles emerge into the flowing layer with zero initial downstream velocity V0= 0 2. Peak acceleration is proportional to the tangential velocity (TV), 3. Particles accelerate over the distance l. 4. Acceleration (a) is not constant over the distance l, but the rate of change in acceleration scales appropriately with the value of l (i.e., a = amaxƒ(x/l), where x is the distance down the cascade). Developing a Model
  • 35.
    9/5/2015 35 Scale upof Powder Blending March 2014 35 of 50 Tehran University of Medical Sciences School of Pharmacy Developing a Model • Using these assumptions a new relation for particle velocity would be: • Which relates particle velocities to the rotation rate and the radius, can be used as the basis for scaling particle velocities with changes in cylinder diameter and rotation rate.
  • 36.
    9/5/2015 36 Scale upof Powder Blending March 2014 36 of 50 Tehran University of Medical Sciences School of Pharmacy Returning to Dimensional Analysis • This equation can be used to complete the dimensional analysis discussed earlier. • Applying dimensional homogeneity and solving leads to:
  • 37.
    9/5/2015 37 Scale upof Powder Blending March 2014 37 of 50 Tehran University of Medical Sciences School of Pharmacy Testing the Model • To test the scaling criteria suggested by equation we will look at velocity profiles between 10 and 30 rpm. Figure shows the scaled velocity profiles (i.e., all data are divided by using RΩ2/3(g/d)1/6, and the distance down the cascade is divided by the cylinder diameter
  • 38.
    9/5/2015 38 Scale upof Powder Blending March 2014 38 of 50 Tehran University of Medical Sciences School of Pharmacy
  • 39.
    9/5/2015 39 Scale upof Powder Blending March 2014 39 of 50 Tehran University of Medical Sciences School of Pharmacy • Un-scaled Data
  • 40.
    9/5/2015 40 Scale upof Powder Blending March 2014 40 of 50 Tehran University of Medical Sciences School of Pharmacy Returning to our example • scaling from a 5-ft3 blender to a 25-ft 3 blender, again the relative change in length is 71%. This time, to scale surface velocities using this approach, the blending speed (Ω) must be reduced by a factor of (1.71)-3/2 = 0.45, corresponding to 6.7 rpm (assuming the particle diameter, d,remains constant). • Again, the total number of revolutions would remain constant at 225, for a blend time of 33.6 min.
  • 41.
    9/5/2015 41 Scale upof Powder Blending March 2014 41 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • Experimental work has not validated the preceding scaling procedure with respect to scale-up of blending processes. • This model should not be favored over other approaches currently in use, though it may provide additional insight.
  • 42.
    9/5/2015 42 Scale upof Powder Blending March 2014 42 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • recent work has indicated that particle velocities may be critical for determining segregation dynamics in double-cone blenders and V- blenders. • Segregation occurs within the blender as particles begin to flow in regular, defined patterns that differ according to their particle size.
  • 43.
    9/5/2015 43 Scale upof Powder Blending March 2014 43 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • In a 1.9-quart-capacity V-blender at fixed filling (50%), incrementally changing rotation rate induced a transition between two segregation patterns • At the lower rotation rate, the “small-out” pattern forms • At a slightly higher rotation rate, the “stripes” pattern forms
  • 44.
    9/5/2015 44 Scale upof Powder Blending March 2014 44 of 50 Tehran University of Medical Sciences School of Pharmacy Segregation Patterns
  • 45.
    9/5/2015 45 Scale upof Powder Blending March 2014 45 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • To validate both the particle velocity hypothesis and our scaling criteria, similar experiments were run in a number of different-capacity V-blenders.
  • 46.
    9/5/2015 46 Scale upof Powder Blending March 2014 46 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • All the vessels are constructed from clear plexiglass, enabling visual identification of segregation patterns. • For these experiments, a binary mixture of sieved fractions of 150 to 250-(nominally 200) and 710- to 840- (nominally 775-) glass beads was used. • A symmetrical initial condition (top-to-bottom loading) is implemented. • The blender is run at constant rotation rate; a segregation pattern was assumed to be stable when it did not discernibly change for 100 revolutions.
  • 47.
    9/5/2015 47 Scale upof Powder Blending March 2014 47 of 50 Tehran University of Medical Sciences School of Pharmacy TESTING VELOCITY SCALING CRITERIA • The transition speeds (rotation rates) were determined for the change from the “small-out” pattern to “stripes” at 50% filling for all the blenders listed • As discussed, the most common methods for scaling tumbling blenders have used one of two parameters, either the Froude number (Fr) or the tangential speed of the blender
  • 48.
    9/5/2015 48 Scale upof Powder Blending March 2014 48 of 50 Tehran University of Medical Sciences School of Pharmacy RECOMMENDATIONS AND CONCLUSIONS • The analysis of particle velocities provides a good first step toward the rigorous development of scaling criteria for granular flow, but it is far from conclusive. • It is important in granular systems to first determine the dynamic variable that governs the process at hand before determining scaling rules • A systematic, generalized approach for the scale-up of granular mixing devices is still far from attainable. Clearly, more research is required both to test current hypotheses and to generate new approaches to the problem.
  • 49.
    9/5/2015 49 Scale upof Powder Blending March 2014 49 of 50 Tehran University of Medical Sciences School of Pharmacy some simple guidelines that can help through the scale-up Make sure that changes in scale have not changed the dominant mixing mechanism in the blender (i.e., convective to dispersive) Number of revolutions is a key parameter, but rotation rates are largely unimportant. When performing scale-up tests, be sure to take enough samples, be wary of how you interpret your samples. One simple way to increase mixing rate is to decrease the fill level. It also reduces the probability that dead zones will form. Addition of asymmetry into the vessel, either by design or baffles, can have a tremendous impact on mixing rate.

Editor's Notes

  • #3 Tumbling blenders are hollow containers attached to a rotating shaft; the vessel is partially loaded with the materials to be mixed and rotated for some number of revolutions. The major advantages of tumbling blenders are large capacities, low shear stresses, and ease of cleaning. Such as V-blenders(Tween Shell blenders), double cone blenders , in-bin blenders , cylinder blender
  • #4 Unfortunately, there is no generally accepted method for approaching this problem; therefore, ad hoc approaches tend to be the rule rather than the exception. Ad hoc is a Latin phrase meaning "for this". It generally signifies a solution designed for a specific problem or task, non-generalizable
  • #6 Many mixing indices are available; however, there is no “general mixing index,” so the choice of index is left to the individual investigator sample size can have a large impact on apparent variability
  • #8 Some blender types have been built asymmetrically (e.g., the slant cone, the offset V-blender) Asymmetry can be “induced” through intelligent placement of baffles
  • #9 tumbling blenders impart very little shear, unless an intensifier bar (I-bar) or chopper blade is used (in some cases, high shear is detrimental to the active ingredient and so is avoided)
  • #10 For instance, in a Vblender, it is preferable to load the vessel either through the exit valve or equally into each shell. adding a small amount early in the loading process could accidentally send most of the material into one shell of the blender and substantially slow the mixing process.
  • #11 Exponential Function: If a principal amount of 1 earns interest at an annual rate of x compounded monthly, then the interest earned each month is x/12 times the current value, so each month the total value is multiplied by (1+x/12), and the value at the end of the year is (1+x/12)12. If instead interest is compounded daily, this becomes (1+x/365)365. Letting the number of time intervals per year grow without bound leads to the limit definition of the exponential function, Approximately 2.718281828 for x=1   e^x = lim nethernity (1+x/n)^n
  • #12 (the critical speed is the speed at which tangential acceleration due to rotation matches the acceleration due to gravity).
  • #14 The Froude number (Fr) is a dimensionless number defined as the ratio of a body's inertia to gravitational forces. In fluid mechanics, the Froude number is used to determine the resistance of a partially submerged object moving through water, and permits the comparison of objects of different sizes. The Froude number is defined as: Fr = v/c where  v is a characteristic velocity, and c is a characteristic water wave propagation velocity. The grater the Fr the more the resistance. Stirred tanks[edit] In the study of stirred tanks, the Froude number governs the formation of surface vortices. Since the impeller tip velocity is proportional to Nd, where N is the impeller speed (rev/s) and d is the impeller diameter, the Froude number then takes the following form: Fr= N2d/g However, Fr is derived from equations based on continuum mechanics, whereas the scale of the physical system for blending of granular materials is on the order of the mean free path of individual particles, which may invalidate the continuum hypothesis. Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. Lagrangian description[edit] In the Lagrangian description the position and physical properties of the particles are described in terms of the material or referential coordinates and time. (sitting in a boat flowing down the river) motion shape is important for us In computational fluid dynamics, the Lagrangian particle tracking (or in short LPT method) is a numerical technique for tracking Lagrangian particles within an Eulerian phase.  The Eulerian description, introduced by d'Alembert, focuses on the current configuration , giving attention to what is occurring at a fixed point in space as time progresses, instead of giving attention to individual particles as they move through space and time. This approach is conveniently applied in the study of fluid flow where the kinematic property of greatest interest is the rate at which change is taking place rather than the shape of the body of fluid at a reference time. (Focusing on a definite point of flowing river) motion rate is important for us
  • #15 geometric similarity (i.e., all angles and ratios of lengths are kept constant)
  • #22 Lord Rayleigh’s sarcastic comment with which he began his short essay on “The Principle of Similitude” [3]: “I have often been impressed by the scanty attention paid even by original workers in physics to the great principle of similitude. It happens not infrequently that results in the form of ‘laws’ are put forward as novelties on the basis of elaborate experiments, which might have been predicted a priori after a few minutes’ consideration.”
  • #27 Figure 2 shows the mean cascading velocity versus distance down the granular cascade for experiments run at the same tangential velocity. Despite a nearly fourfold difference in diameter, the velocity data all fall on nearly the same curve over the first 3 cm down the flowing layer. This agreement indicates that initial particle accelerations may be nearly equivalent, regardless of vessel size.
  • #31 While the data clearly display curvature, this linear fit is used as a first-order approximation for scaling purposes.
  • #35 Acceleration has been shown, though, to vary along the length of the flowing region. Also, the distance to reach zero acceleration depends on the rotation rate. It may be possible, however, to scale peak velocities using Eq. (6) subject to some simplifying assumptions
  • #44 A quart (quarter of a gallon) =  0.946352946 litres
  • #48 The RΩ2/3(g/d)1/6 parameter gives much better agreement than either Fr or tangential velocity; the relative standard deviation for R(2/3(g/d)1/6 is 8.5%, compared to 89% for Fr and 30% for tangential velocity.