The document presents information on the Poisson distribution: - It defines the Poisson distribution as a discrete probability distribution used for situations where events occur rarely and independently. - Properties of the Poisson distribution are discussed, including that it has one parameter (m), and the mean and variance are equal to m. - Examples of when the Poisson distribution can be applied are given, such as counting defects, bacteria, phone calls, or road accidents. - Steps for applying the Poisson distribution formula and fitting observed data to a Poisson distribution are outlined.

1. Presentation on topic : What
is Poisson distribution ? Give
examples where it can be
applied.
Presented by :
Sangeeta Saini
M.Com (p)
641

2. Poisson Distribution.
Definition of Poisson
Distribution.
Properties of Poisson
distribution.
Examples of Poisson
distribution.

3. Poisson Distribution
 Poisson Distribution is a discrete probability
distribution and it is widely used in
statistical work . This distribution was
developed by French mathematician Dr.
Simon Denis Poisson in 1837 and the
distribution is named after him.
 The Poisson Distribution is used in those
situations where the probability of
happening of an event is small ,i.e. the event
rarely occurs.

4. DEFINITION OF POISSON DISTRIBUTION
 Poisson Distribution is defined and given by
the following probability function:
 Where P(X=x ) = probability of obtaining x
number of success.
 m=np = parameter of distribution .
 e = 2.7183 base of natural logarithms
P(X=x) = e-m .mx
X!

5. Number of success (X) Probability P(X)
0 e-m.m0=e-m
1 e-1.m1 =me-m
2
e-2.m2 =m2e-m
2! 2
.
.
.
.
.
.
.
.
.
.
x e-m.mx
x!
0!
1!

6. Properties of
Poisson Distribution
Discrete probability
distribution
•The Poisson
distribution is a
discrete
probability
distribution in
which the number
of success are
given in whole
number such as ,
0,1,2,……… etc.
Value of p and q
•Poisson
distribution is
used in those
situations where
the probability of
occurrence of an
event is very small
(p-0) and
probability of non
occurrence of
event is very large
(q-1).
Main parameter
•It has only one
parameter m and
its value is equal
to np
•m= np
Constant of Poisson
distribution
•The constant of
Poisson
distribution can be
obtained by from
following formula:
•Mean =m= np
•Variance =m
•S.D.= root of m
•Moment coeff. Of
skewness = 1/ root
of m
•Moment coeff. Of
kurtosis = 3+ 1/m
Equality of mean
and variance
•Its mean and
variance are
equal.
•Mean = variance

7. Examples of Poisson Distribution
It is used in statistical quality control to count the number of defects of an item.
In Biology, to count the number of bacteria.
In insurance problems to count the number of casualities.
To count the number of errors per page in a typed material .
To count the number of incoming telephone calls in a town.
To count the number of defective blades in a lot of manufactured blades in a factory.
To count the number of deaths at a particular crossing in a town as a result of road
accident.
To count the number of suicides committed by lover point in a year.

8. Applications of
Poisson Distribution
Application of
Poisson
distribution
formula
Fitting of
Poisson
distribution

9. Application of Poisson distribution
formula
When the value of p is given.
Example : It is given that 2% of the screw manufactured by a
company are defective. Poisson distribution to find the
probability that a packet of 100 screws contains : (a) no
defective screws (b) one defective screw (c) two or more
defectives.{ Given : e-2= 0.135 }
Solution : let p = probability of defective screw = 2 % = 2/100
n=100
m=n.p
100×2/100 =2 , m=2
(a) No defective screw
P(X=x) = e-m .mx ÷ x!
P(X=0) = e-2. 20 ÷ 0!
= e-2 =0.135

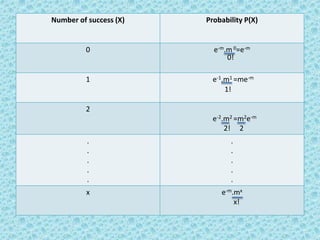
10. (b) P(one defective )
P(X=1) = e-2. 21÷ 1!
= e-2×2
= 0.135 × 2 = 0.270
(c)P ( two or more defectives)
=1- [P(0)+P(1)]
= 1-[0.135+0.270]
= 1-0.405
= 0.595

11. When the value of m is given
Example : Between the hours of 2 P.M. to 4 P.M., the average
number of phone calls per minute coming into a switch board of
company is 2.5. find the probability that during one particular
minute there will be : (a) no phone call at all . (b)exactly 3 calls.
(Given e-2 = 0.1353 , e-0.5 = 0.6065 )
Solution : average number of phone calls =m=2.5
P(X=x) = e-m .mx ÷ x!
(a) P(no call) =P(X=0) = e-2.5. 2.50÷ 0! = e-2.5
e-2.5= e-2.e-0.5
= 0.1353 ×0.6065
= 0.0821
(b) P( exactly 3 calls) =P(X=3) = e-2.5. 2.53÷ 3!
= (0.0821).(15.625)/ 3×2×1
= 0.2138

12. Fitting of a Poisson Distribution
Step 1. firstly , we compute mean from the observed frequency data .
Mean = /N
Step 2. the value of e-m is obtained . If the value of e-m is not given in the
question .
e-m = Reciprocal [ Antilog (m × 0.4343)]
Step 3. then ,we compute the probability of 0,1 , 2, 3 or x success by using
Poisson distribution.
P(X=x) = e-m .mx ÷ x!

13. Step 4. the expected frequency are then obtained by multiply each probability with
n , total frequencies.
Number of successes (X) Probability P(X) Expected frequency Fe
(X)
0 e-m.m 0=e-m
0!
N.P(0) =Ne-m
1 e-1.m1 =me-m
1!
N.P(1)= N.me-m
2
e-2.m2 =m2e-m
2! 2
N.P(2)= N. m2e-m
2
.
.
.
.
.
.
.
.
.
.
.
x e-m.mx
x!
N.P(X)= N. e-m.mx
X!

14. Deaths 0 1 2 3 4
Frequency 109 65 22 3 1
Also find mean and variance of above distribution.
Solution : Fitting of Poisson distribution
Deaths Frequency (f) fX
0 109 0
1 65 65
2 22 44
3 3 9
4 1 4
200 122

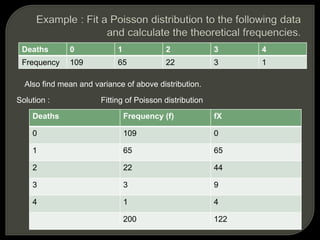
15. Mean = 122 /200 = 0.61
m= 0.61
Now obtain the value of e-0.61
e-m = Reciprocal [ Antilog (m× 0.4343)]
Putting m=0.61
e-m = Reciprocal [ Antilog (0.61× 0.4343)]
= Rec. [antilog(0.26492)]
= Rec. [1.841]
=0.5432

16. No. of deaths probability Expected frequency
0 P(0)=e-0.61(0.61)0/0! =e-
0.61= 0.5432
N.P(0)=200×0.5432 =
108.64 = 109
1 P(1)=e-0.61(0.61)1/1! =e-
0.61×0.61= 0.5432× 0.61 =
0.33
N.P(1)=200×0.33=66
2 P(2)=e-0.61(0.61)2/2! = 0.10 N.P(2)=200×0.10=20
3 P(3)=e-0.61(0.61)3/3! =
0.021
N.P(3)=200×0.021=4.2=4
4 P(4)=e-0.61(0.61)4/4! =
0.0031
N.P(4)=200×0.0031=0.62=
1
Thus
X 0 1 2 3 4
Fe 109 66 20 4 1
Mean= 0.61
Mean= variance =0.61

17. Conclusion
In conclusion ,we can say that ,
the Poisson Distribution is useful
in rare events where the
probability of success (p) is very
small and probability of failure
(q) is very large and value of n is
very large.