Download to read offline
JW
Uploaded byJAVAID AHMAD WANI
PPTX, PDF355 views
Poisson distribution presentation
The Poisson distribution, derived by Siméon Poisson in 1837, describes the probability of rare events occurring within a fixed interval. It is applicable in situations where the event count is discrete, trials are large, and the success probability is small. The document also contrasts Poisson distribution with the binomial distribution and provides examples and calculations for understanding its application.
In this document
Powered by AI
Presentation introduces the Poisson Distribution and its relevance in statistics.
The Poisson distribution was derived by Siméon Poisson in 1837, initially applied to horse-kicking deaths.
Used for rare events; examples include defective screws, printing mistakes, and air accidents.
Formulation conditions include discrete random variables, large trials, and statistical independence.
Introduces the equation for calculating probabilities using Poisson Distribution with constant e.
Calculates the probability of 3 customers arriving tomorrow based on the Poisson distribution.
Determines the probability of finding at least one defective fuse in a box of 200.
Thank you slide, closing the presentation.
Calculates the probability of exactly 2 accidents in a month at an intersection using Poisson.
Describes calculations for mean, variance, and standard deviation in Poisson distribution.
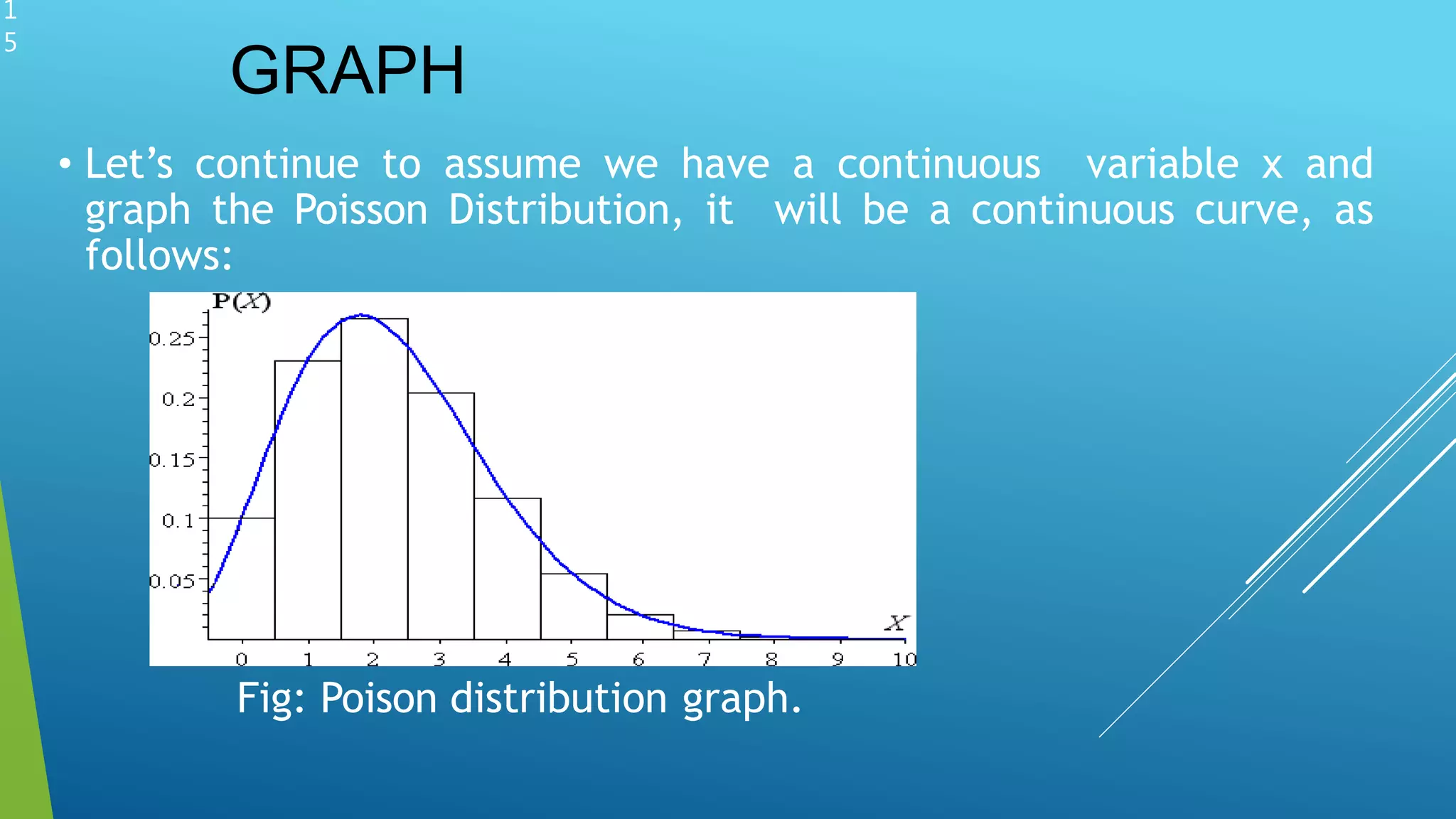
Displays a graph of the Poisson distribution representing data visually.
Discusses differences between Binomial and Poisson distributions in their applications.
