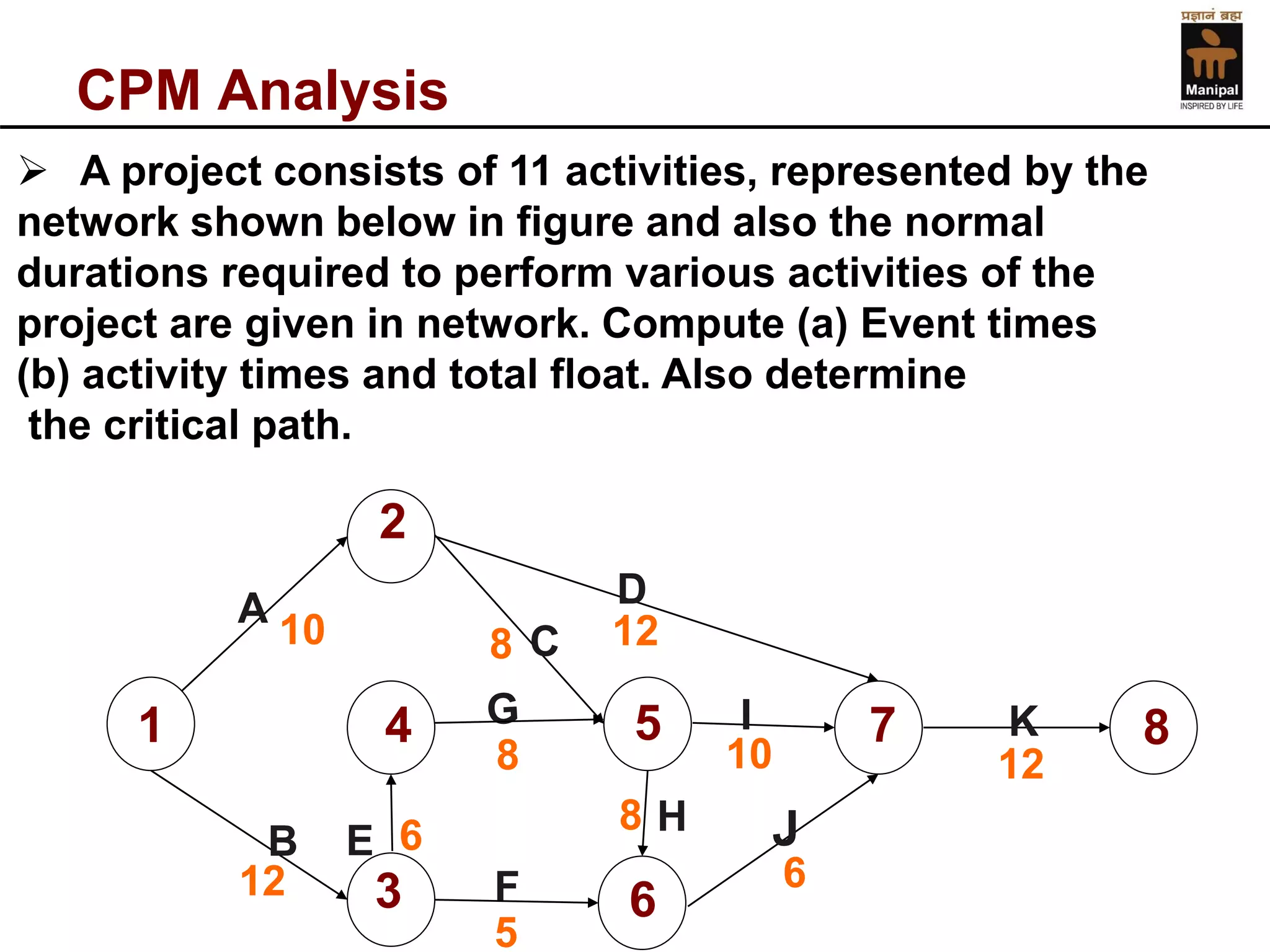
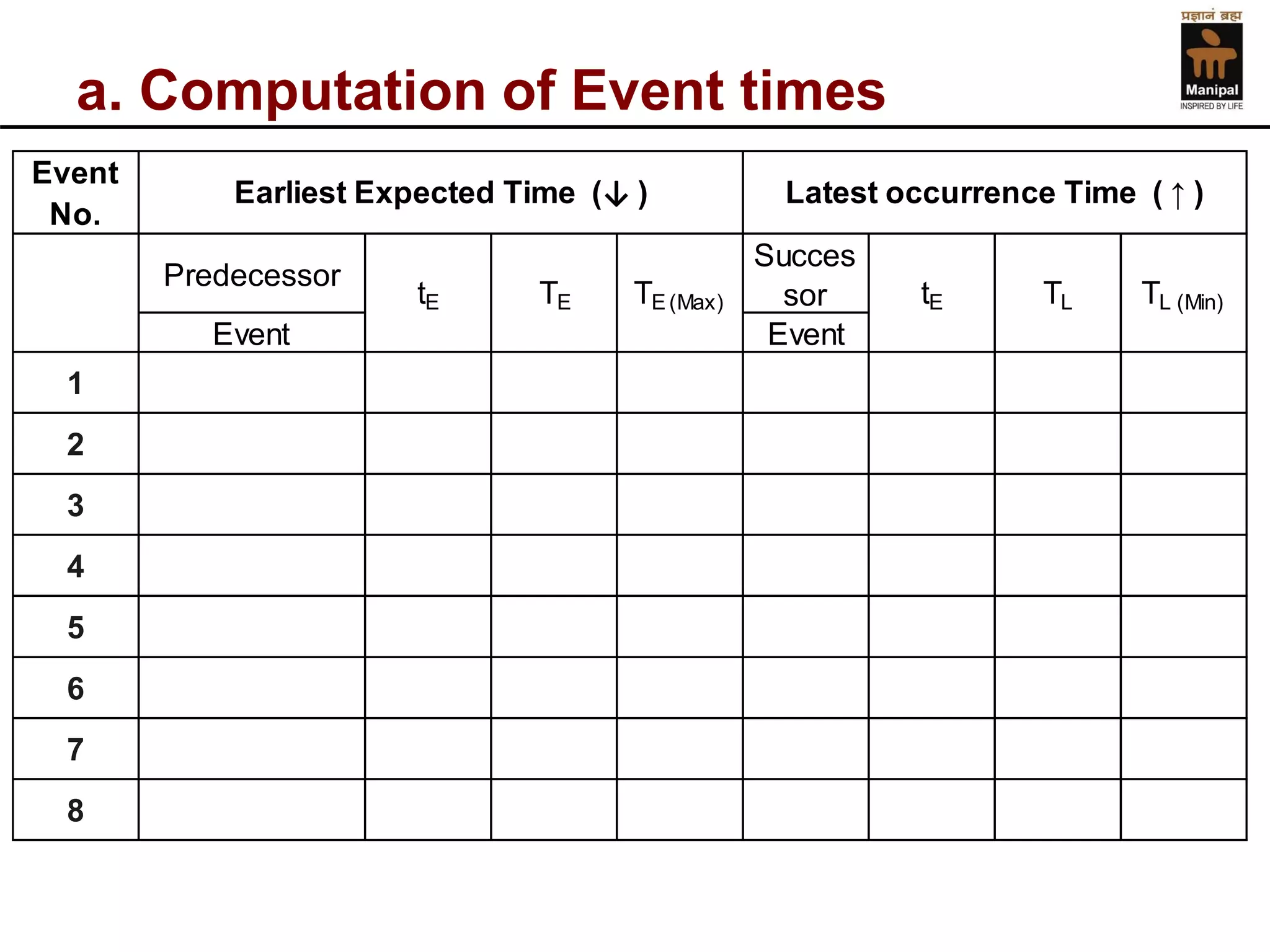
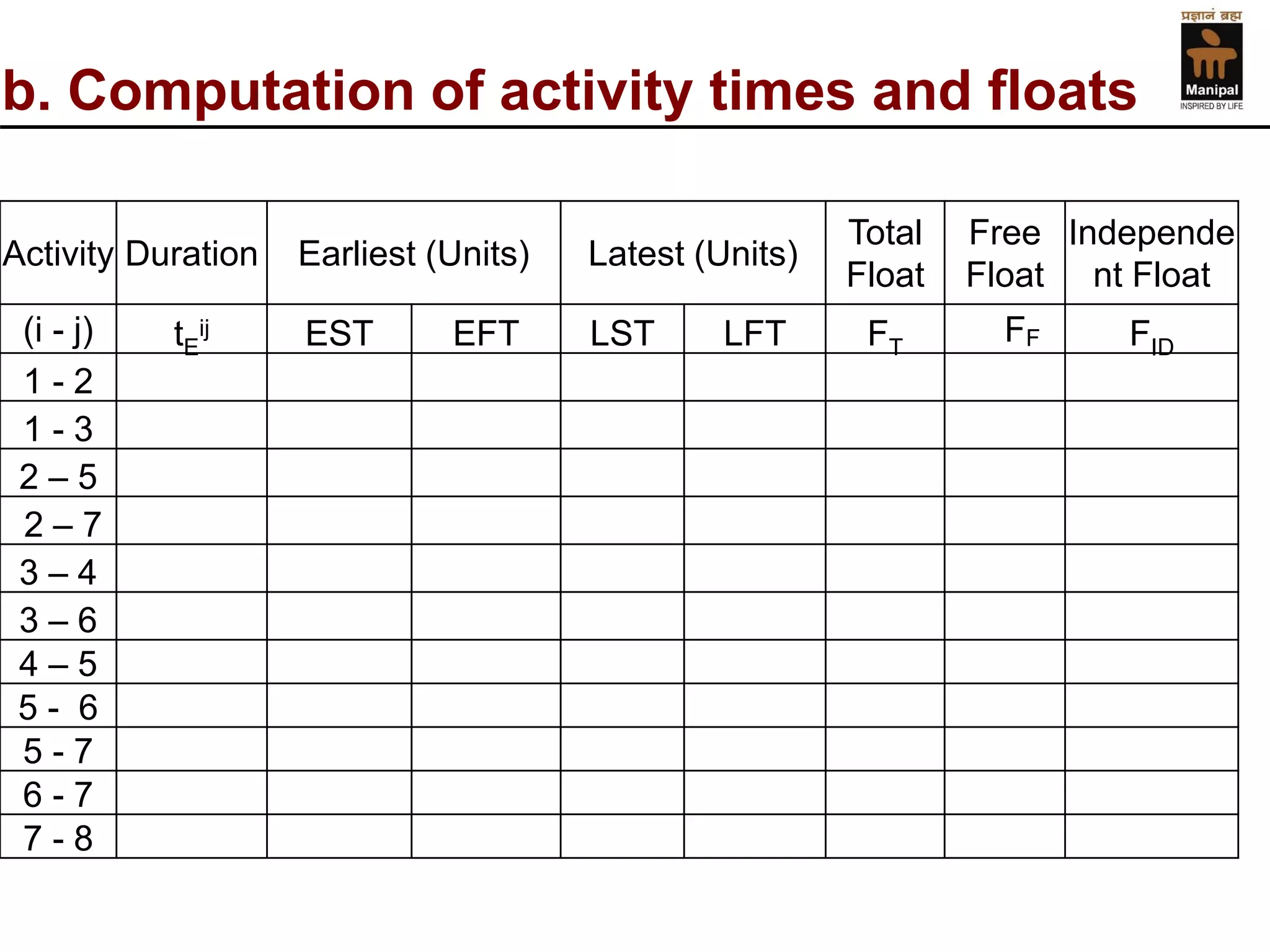
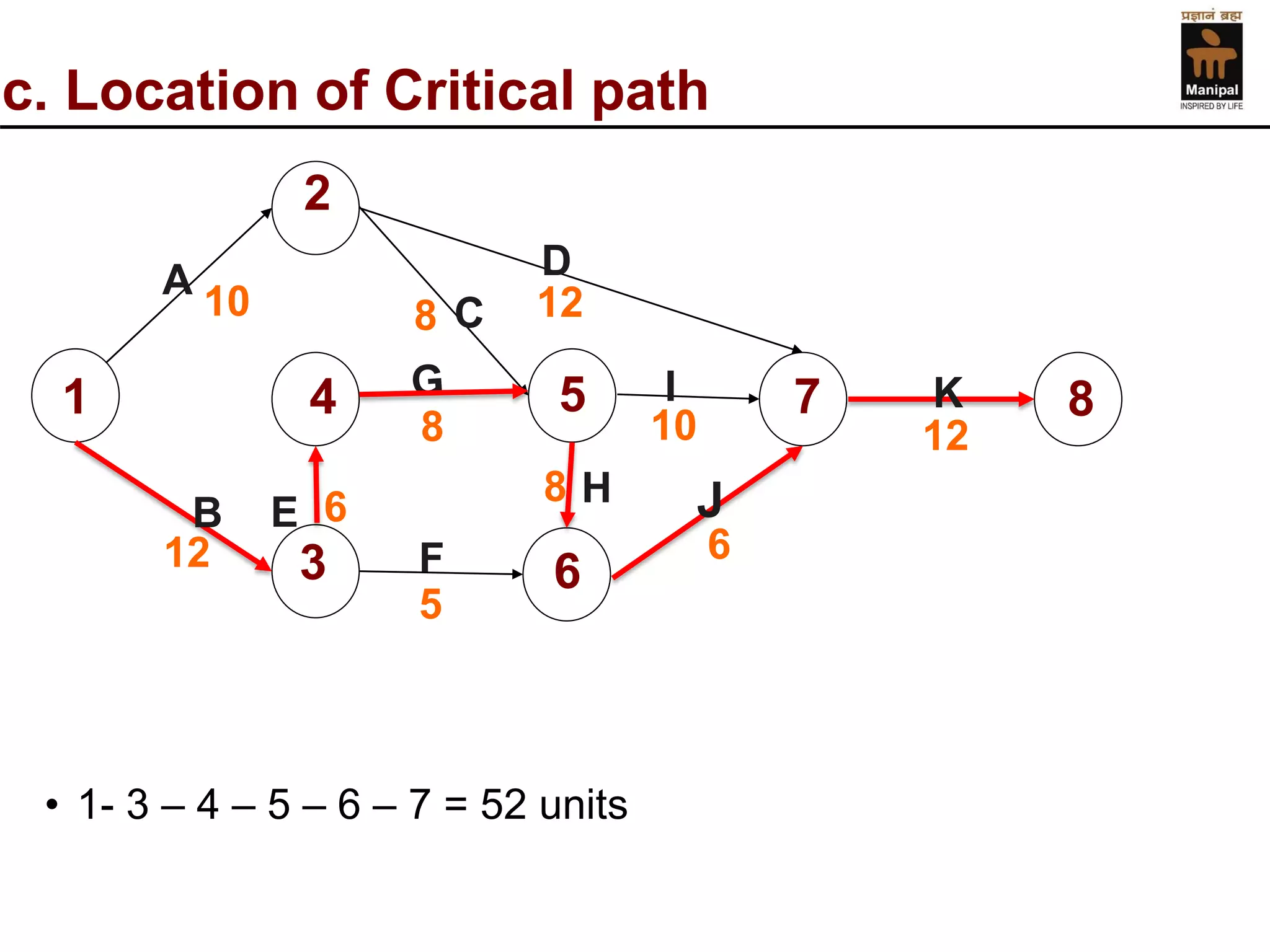
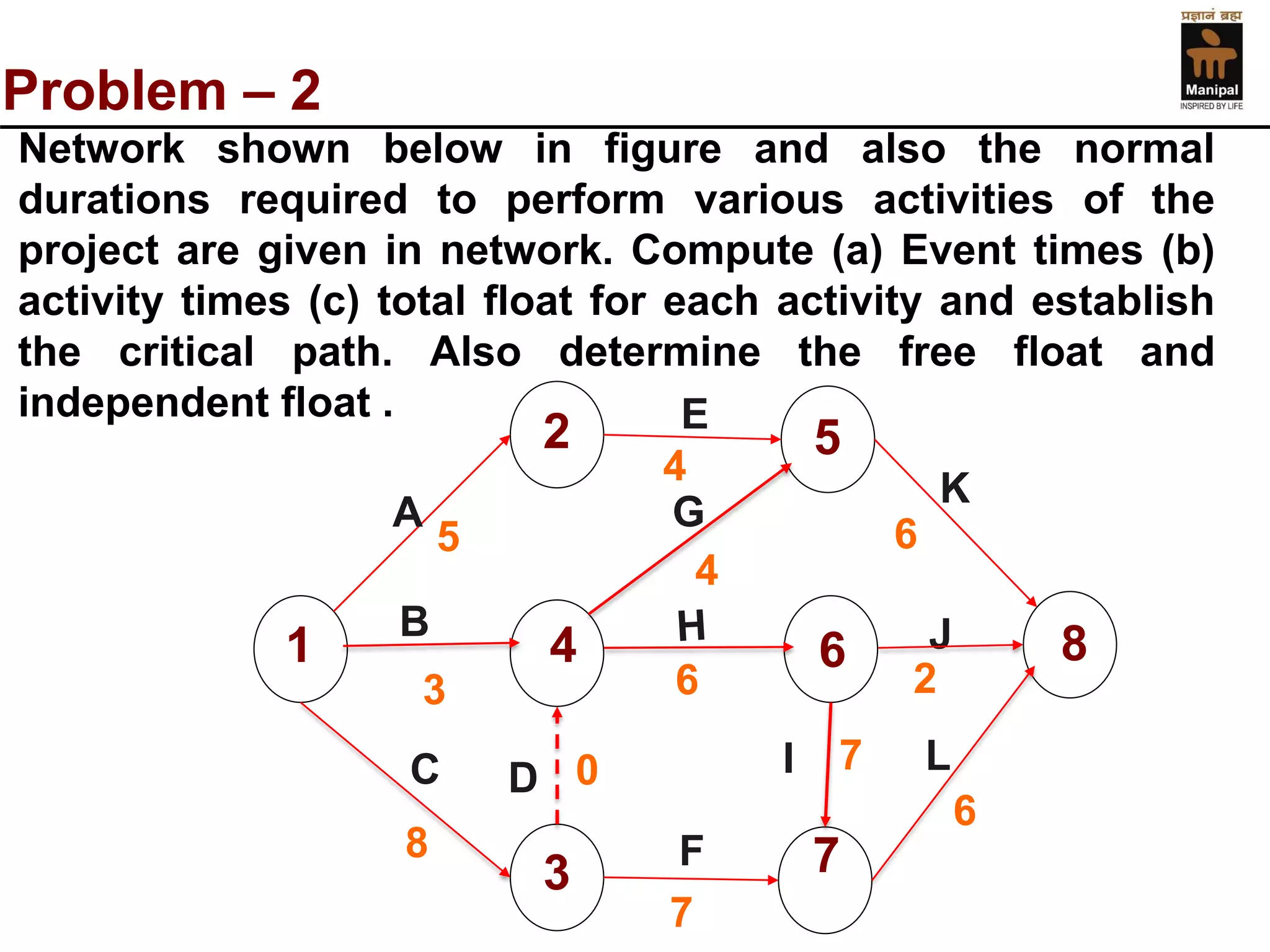
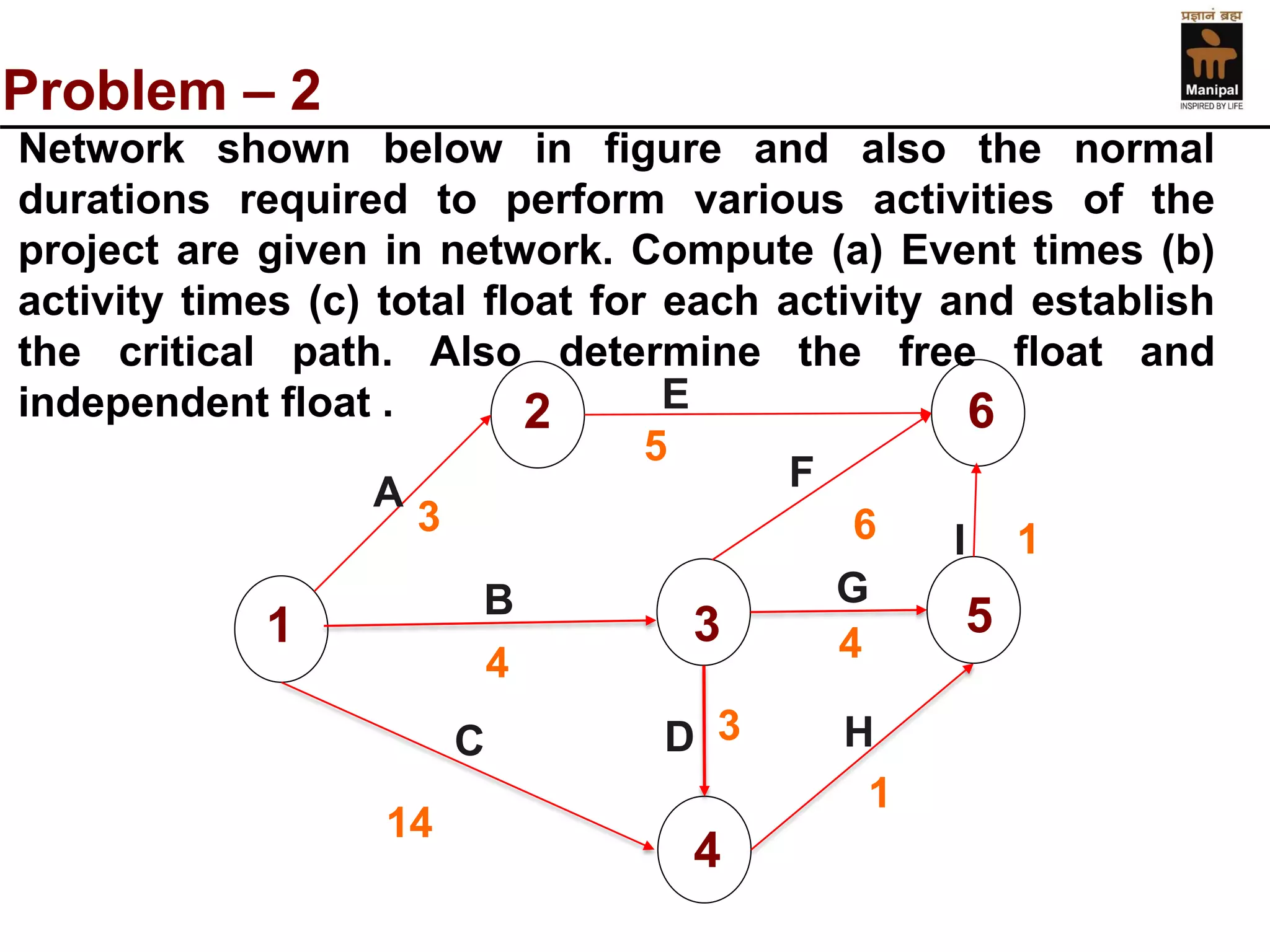
This document provides information about critical path method (CPM) including: - An introduction to CPM and examples of projects where it can be applied. - The differences between CPM and PERT. - Key terms and definitions used in CPM like activity times, floats, and critical path. - An example of calculating event times, activity times, floats, and determining the critical path for a sample CPM network diagram.

1. Chapter –6
Critical Path Method (CPM)
Course Code -CIE 403
Mr. Ramesh Nayaka, (M.Tech. –IIT Madras)
Assistant Professor
Department of Civil Engineering
Manipal Institute of Technology, Manipal -576104
Karnataka, India

2. Content…
•Introduction to CPM
•Difference between CPM and PERT
•Terms and Definitions
•Calculation of Float
•Critical Path

3. Introduction to CPM
CPM network are usually used for repetitive type of projects, where fairly accurate estimates of time can be made for the activities of the project.
The activities of these projects are characteristically subject to relatively small amount of variation. Hence CPM is not suitable for research and development type of projects.
Examples from fairly diverse field where application of CPM can be made:
Building a new bridge across river ganga, Constructing a multi-storeyed building, extension of a factory building, shifting a manufacturing unit to other site and manufacturing of a new car etc.

4. Difference between CPM and PERT
CPM
PERT
Activity Oriented network
Event oriented network
The time estimatesare of a fair degree of accuracy
Time estimates are not that accurate andthere is an uncertainty attached to it
Follows deterministic approach
Followsprobabilistic approach
Cost is governingfactor
Time is governing factor
Project duration is so fixed such that the cost is minimum
Assumed that cost is directly proportional to time so time is reduced maximum possible to enjoy least cost
Critical path is thatpath which joins the critical activities
Criticalpath is the path which joins the critical events

5. Terms and Definitions
Activity Times
Forward Passing :
Earliest Start Time (EST) :earliest time by which an activity start
EST = earliest event time of tail event = TEi
Earliest Finish Time (EFT) : Earliest time by which an activity can be completed
EFT = EST + tEij= TEi + tEij

6. Terms and Definitions
Activity Times
Backward Passing :
Latest Finish Time (LFT) : latest time by which an activity can completed without delaying the completion of the project
LFT = Latest Finish Time of head event = TLj
Latest Start Time (LST) : latest time by which an activity can start without delaying the completion of the project
LST = LFT -tEij= TLj -tEij

7. Terms and Definitions
FLOATS
Similar to slack in PERT
Associated with activity times
Denotes flexibility range within which the activity start and finish time may fluctuate without affecting the total duration of the project

8. Terms and Definitions
TYPES OF FLOATS
Total Float (FT) : timespan by which starting or finishing of an activity can be delayed without affecting the overall completion time of the project.
It refers to the amount of time by which the completion of activity could be delayed beyond earliest expected completion time without affecting overall project duration time
FT= LST –EST or LFT -EFT

9. Terms and Definitions
TYPES OF FLOATS
Free Float (FF) : duration by which an activity can be delayed without delaying any other succeeding activity.
It refers to the amount of time by which the completion of an activity can be delayed beyond the earliest finish time without affecting the earliest start time of a subsequent succeeding activity.
This float is concerned with the commencement of subsequent activity
FF= FT–Sj , Sj= Slack of head event = TLj –TEj

10. Terms and Definitions
TYPES OF FLOATS
Independent Float (FID): It is excess time available if the preceding activity ends as late as possible and the succeeding activity starts as early as possible
It is refers to that the amount of time by which the start of an activity can be delayed, without affecting earliest start time of any immediately following activities
This float concerned with prior and subsequent activities
FID= FF–Si
Si = slack of tail event =TLi–TEi

11. Terms and Definitions
TYPES OF FLOATS
Interfering Float (FIT) : Another name for head event slack (Sj), it is the difference between total float and free float
FIT= FT–FF = TLj –TEj = Sj
Note : if the total float (FT) for any activity is zero then such activity is called critical activity
Critical Activity : an activity is said to be critical, if a delay in its start cause a further delay in the completion of the entire project

12. Terms and Definitions
Critical Path : The sequence of critical activities in a network which determines the duration of a project is called critical path.
•It is the longest path in the network from the starting event to the ending event
•For activities lies on critical path
EST =LST , EFT = LFT and EST –EFT = LST –LFT
Sub critical activity : When total float (FT ) is positive
Critical Activity :When total float (FT ) is zero
Super critical activity : When total float (FT ) is negative

13. Calculating Critical Path & Float for a Network Diagram
Find out the length of all the paths in the network diagram
The longest path is the critical path
Float = EF –LF = ES -LS

14. Terms and Definitions
Critical Path : The sequence of critical activities in a network which determines the duration of a project is called critical path.
•It is the longest path in the network from the starting event to the ending event
•For activities lies on critical path
EST =LST , EFT = LFT and EST –EFT = LST –LFT
Sub critical activity : When total float (FT ) is positive
Critical Activity :When total float (FT ) is zero
Super critical activity : When total float (FT ) is negative

15. Terms and Definitions
Critical Path : The sequence of critical activities in a network which determines the duration of a project is called critical path.
•It is the longest path in the network from the starting event to the ending event
•For activities lies on critical path
EST =LST , EFT = LFT and EST –EFT = LST –LFT
Sub critical activity : When total float (FT ) is positive
Critical Activity :When total float (FT ) is zero
Super critical activity : When total float (FT ) is negative

16. CPM Analysis
F
1
2
4
3
5
6
7
8
A
B
C
D
E
H
K
J
I
10
8
12
8
10
6
5
12
6
12
8
Aprojectconsistsof11activities,representedbythe
networkshownbelowinfigureandalsothenormal
durationsrequiredtoperformvariousactivitiesofthe
projectaregiveninnetwork.Compute(a)Eventtimes
(b)activitytimesandtotalfloat.Alsodetermine
thecriticalpath.

17. a. Computation of Event times Event No. PredecessorSuccessorEventEvent12345678Earliest Expected Time (↓ )Latest occurrence Time ( ↑ ) tETETE (Max)tETLTL (Min)

18. b. Computation of activity times and floats
Activity
Duration
Earliest (Units)
Latest (Units)
Total Float
Free Float
Independent Float
(i -j)
tEij
EST
EFT
LST
LFT
FT
FF
FID
1 -2
1 -3
2 –5
2 –7
3–4
3–6
4–5
5 -6
5 -7
6 -7
7 -8

19. c. Location of Critical path
•1-3 –4 –5 –6 –7 = 52 units
F
1
2
4
3
5
6
7
8
A
B
C
D
E
H
K
J
I
10
8
12
8
10
6
5
12
6
12
8

20. Problem –2
F
1
2
4
3
5
6
7
8
A
B
G
E
D
I
L
J
5
4
4
6
2
6
7
8
0
6
7
C
K
3
Networkshownbelowinfigureandalsothenormaldurationsrequiredtoperformvariousactivitiesoftheprojectaregiveninnetwork.Compute(a)Eventtimes(b) activitytimes(c)totalfloatforeachactivityandestablishthecriticalpath.Alsodeterminethefreefloatandindependentfloat.

21. Problem –2
1
2
3
6
4
5
A
B
E
D
G
H
3
5
3
1
14
4
C
F
4
Networkshownbelowinfigureandalsothenormaldurationsrequiredtoperformvariousactivitiesoftheprojectaregiveninnetwork.Compute(a)Eventtimes(b) activitytimes(c)totalfloatforeachactivityandestablishthecriticalpath.Alsodeterminethefreefloatandindependentfloat.
6
1
I