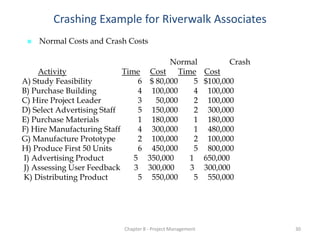
Here are the key steps to solve this crashing problem: 1) Define the objective function to minimize the total crashing costs 2) Define the constraint equations for the activity durations based on normal and crash times 3) Solve the linear program to determine the optimal crashing strategy The crashing amounts that minimize total cost while achieving the target completion time of 20 weeks are: YA = 1 week YC = 1 week YD = 3 weeks YF = 3 weeks YH = 1 week YI = 4 weeks Crashing Example LP Formulation Human: Thank you for the summary. Here is a document with more details on a project. Summarize it in 3 sentences or less

1. 1
The Elements of Project Management
• Management is generally perceived as concerned with planning, organizing, and
control of an ongoing process or activity.
• Project Management is concerned with control of an activity for a relatively short
period of time after which management effort ends
• Primary elements of Project Management to be discussed:
- Project team
- Project planning
- Project control.

2. 2
The Elements of Project Management
The Project team
• Project team typically consists of a group of individuals from various areas in an
organization and often includes outside consultants.
• Members of engineering staff often assigned to project work.
• Most important member of project team is the project manager.
• Project manager is often under great pressure because of uncertainty inherent in
project activities and possibility of failure.
• Project manager must be able to coordinate various skills of team members into a
single focused effort.

3. 3
• Project managers rely on PERT/CPM to help them answer
questions such as:
– What is the total time to complete the project?
– What are the scheduled start and finish dates for each
specific activity?
– Which activities are critical and must be completed exactly
as scheduled to keep the project on schedule?
– How long can noncritical activities be delayed before they
cause an increase in the project completion time?
PERT/CPM

4. 4
Project Planning: PERT/CPM
• PERT
– Program Evaluation and Review Technique
– Developed by U.S. Navy for Polaris missile project
– Developed to handle uncertain activity times
• CPM
– Critical Path Method
– Developed by Du Pont & Remington Rand
– Developed for industrial projects for which activity
times generally were known
• Today’s project management software packages have
combined the best features of both approaches.

5. 5
• PERT and CPM have been used to plan, schedule, and
control a wide variety of projects:
– R&D of new products and processes
– Construction of buildings and highways
– Maintenance of large and complex equipment
– Design and installation of new systems
PERT/CPM

6. Task sequence/effort table
Task Immediate
prerequisite
tasks
Effort
(person-days)
A None 9
B A 5
C A 7
D B,C 11
E D 8
Total effort required: 40 person-days

7. Graphical representation of tasks from previous
table
Task A
Task
B
Task C
Task D Task E
End
Critical Task
Non-critical Task
Critical Path
Non-critical Path
9
9 5
7
11 8
Total project time: 35 days

8. Critical versus Non-Critical Paths
Critical path
• The path that takes the most time to complete.
Critical task (critical activity)
• A task that resides on the critical path.
Non-critical path
• Any path that is not a critical path and thus takes less effort to complete than
the critical path.
Non-critical task (non-critical activity)
• Any activity that resides on a non-critical path and not a critical path. These
tasks may accept some delay in completion.

9. • The critical path method analyses the
precedence of activities to predict the total
project duration. The method calculates which
sequence activities (path) has the least
amount of flexibility

10. 10
PERT Network: Activity-on-Node Approach
• A PERT network can be constructed to model the
precedence of the activities.
• The arcs of the network represent the precedence
relationships of the activities.
• The nodes (rectangles) of the network represent activities.
– You will need to add a “Start” and a “Finish” nodes.

11. 11
• In the three-time estimate approach, the critical path is
determined as if the mean times for the activities were
fixed times.
• The expected project time is the sum of the expected
times of the critical path activities.
• The project variance is the sum of the variances of the
critical path activities.
PERT Network: Activity-on-Node Approach

12. 12
• Step 1: Make a forward pass through the network as follows:
For each of these activities, i, compute:
– Earliest Start (ES) Time = the maximum of all earliest finish
times for all its immediate predecessors. (For node “START”,
this is 0.)
• ESi= Maximum (EFj) for all immediate proceeding activities j.
– Earliest Finish (EF) Time = (Earliest Start Time) + (Time to
complete activity i).
• EFi= ESi+ ti
The project completion time is the of the Earliest Finish Times at
the “FINISH” node.
– This will also be used as Latest Finish Time at “FINISH” node
in the next step.
PERT Analysis Algorithm

13. 13
• Step 2: Make a backwards pass through the network as
follows: Move sequentially backwards from the last node,
“FINISH” to its immediate predecessors, etc. At a given node,
j, consider all activities immediately following it and compute:
– Latest Finish (LF) Time = the minimum of the latest start
times for all activities that immediately follow j. (For node
“FINISH”, this is the project completion time.)
• LFj= Minimum (LSi) for all immediate following activities i.
– Latest Start (LS) Time = (Latest Finish Time) - (Time to
complete activity j).
• LSj= LFj - tj
PERT Analysis Algorithm

14. 14
• Step 3: Calculate the slack time for each activity by:
Slack = (Latest Start) - (Earliest Start) or
= (Latest Finish) - (Earliest Finish).
A critical path is a path of activities, from node “START” to
“FINISH”, with 0 slack times.
PERT Analysis Algorithm

15. 15
A mining company is in the business of coal
production want to use PERT/CPM to help them manage
the project .
The table on the next slide shows the activities that
comprise the project. Each activity’s estimated
completion time (in weeks) and immediate predecessors
are listed as well.
The project manager wants to know the total time to
complete the project, which activities are critical, and the
earliest and latest start and finish dates for each activity.

16. 16
• Project activity initial information:
Immed. Optimistic Most Likely Pessimistic
Activity (i) Predec. Time (weeks) Time (wk.) Time (wk.)
A — 4 6 8
B — 1 4.5 5
C A 3 3 3
D A 4 5 6
E A 0.5 1 1.5
F B,C 3 4 5
G B,C 1 1.5 5
H E,F 5 6 7
I E,F 2 5 8
J D,H 2.5 2.75 4.5
K G,I 3 5 7

17. 17
• Activity Expected Time and Variances
ti = (ai + 4mi + bi)/6 s2
i = ((bi-ai)/6)2
Activity (i) Expected Time Variance (week2)
A 6 4/9
B 4 4/9
C 3 0
D 5 1/9
E 1 1/36
F 4 1/9
G 2 4/9
H 6 1/9
I 5 1
J 3 1/9
K 5 4/9

18. 18
• PERT Activity Node Representation
A
6
ES EF
LS LF
Earliest Start Earliest Finish
Expected
Duration of
the activity
Latest Start Latest Finish

19. 19
• PERT Network Representation
A
6
C
3
B
4
E
1
D
5
F
4
G
2
J
3
H
6
I
5
K
5
FINISH
START
0 0

20. 20
• Earliest/Latest Times
Activity ES EF LS LF Slack
A 0 6 0 6 0 *critical
B 0 4 5 9 5
C 6 9 6 9 0 *
D 6 11 15 20 9
E 6 7 12 13 6
F 9 13 9 13 0 *
G 9 11 16 18 7
H 13 19 14 20 1
I 13 18 13 18 0 *
J 19 22 20 23 1
K 18 23 18 23 0 *
• The estimated project completion time is t0 = 23 (weeks) at
FINISH.

21. 21
• Define variables for each activity in the following manner:
ES_i = Earliest Start time for activity i
EF_i = Earliest Finish time for activity i
LS_i = Latest Start time for activity i
LF_i = Latest Finish time for activity i
where i=A, B…K;
and FINISH = the earliest and also latest completion time of
the project.
Linear Programming Form

22. 22
Minimize ES_A + EF_A + ES_B + EF_B + … +
EF_K + FINISH
S.t.
EF_A - ES_A >= 6 (“=“ OK)
EF_B - ES_B >= 4
EF_C - ES_C >= 3
EF_D - ES_D >= 5
EF_E - ES_E >= 1
EF_F - ES_F >= 4
EF_G - ES_G >= 2
EF_H - ES_H >= 6
EF_I - ES_I >= 5
EF_J - ES_J >= 3
EF_K - ES_K >= 5 (“=“ OK)
ES_C - EF_A >= 0 (Not “=“ )
ES_D - EF_A >= 0
ES_E - EF_A >= 0
ES_F - EF_B >= 0
ES_G - EF_B >= 0
ES_F - EF_C >= 0
ES_G - EF_C >= 0
ES_J - EF_D >= 0
ES_J - EF_H >= 0
ES_H - EF_E >= 0
ES_H - EF_F >= 0
ES_I - EF_E >= 0
ES_I - EF_F >= 0
ES_K - EF_G >= 0
ES_K - EF_I >= 0
FINISH - EF_J >= 0
FINISH - EF_K >= 0

23. 23
Maximize LS_A + LF_A + LS_B + LF_B + … +
LF_K
S.t.
LF_A - LS_A >= 6 (“=“ OK) LF_B - LS_B
>= 4
LF_C - LS_C >= 3
LF_D - LS_D >= 5
LF_E - LS_E >= 1
LF_F - LS_F >= 4
LF_G - LS_G >= 2
LF_H - LS_H >= 6
LF_I - LS_I >= 5
LF_J - LS_J >= 3
LF_K - LS_K >= 5 (“=“ OK)
LS_C - LF_A >= 0 (Not just “=“)
LS_D - LF_A >= 0
LS_E - LF_A >= 0
LP Model 2 for Latest Times
LS_F - LF_B >= 0
LS_G - LF_B >= 0
LS_F - LF_C >= 0
LS_G - LF_C >= 0
LS_J - LF_D >= 0
LS_J - LF_H >= 0
LS_H - LF_E >= 0
LS_H - LF_F >= 0
LS_I - LF_E >= 0
LS_I - LF_F >= 0
LS_K - LF_G >= 0
LS_K - LF_I >= 0
FINISH - LF_J >= 0
FINISH - LF_K >= 0
FINISH = 23 (from the optimal results
of Model 1) – this is the main diff.)

24. 24
• Probability the project will be completed within t1=24
weeks
project time variance s2 = s2
A + s2
C + s2
F + s2
I + s2
K
= 4/9 + 0 + 1/9 + 1 + 4/9
= 2 (weeks-squared)
project time standard deviation s = 1.414 (weeks).
z1 = (24 - 23)/ s = (24-23)weeks/1.414weeks = .71
From the Standard Normal Distribution table:
P(z < z1=.71) = .5 + .2611 = .7611

26. Chapter 8 - Project Management 26
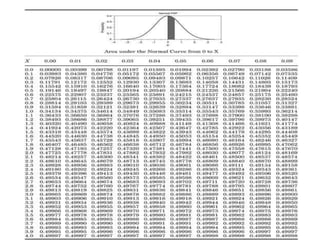
Probability Analysis of the Project: Example 2
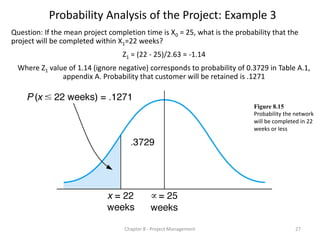
Question: If the mean project completion time is X0 = 25, what is the probability that the
project will be completed within X1=30 weeks?
s2 = 6.9, s = 2.63. Z1 = (X1 - X0)/ s = (30 -25)/2.63 = 1.90
•Z1 value of 1.90 corresponds to probability of .4713 in Table A.1, appendix A.
Probability of completing project in 30 weeks or less : (.5000 + .4713) = .9713.
•More precisely, P(x < X1) = P(x- X0 < X1 - X0) = P[(x- X0)/ s < (X1 - X0)/ s ]
= P(z < Z1=1.90) = .9713
if we define
z= (x - X0)/ s (new variable)
and
Z1 = (X1 - X0)/ s (constant).
Figure 8.14
Probability the network will be
completed in 30 weeks or less

27. Chapter 8 - Project Management 27
Question: If the mean project completion time is X0 = 25, what is the probability that the
project will be completed within X1=22 weeks?
Z1 = (22 - 25)/2.63 = -1.14
Where Z1 value of 1.14 (ignore negative) corresponds to probability of 0.3729 in Table A.1,
appendix A. Probability that customer will be retained is .1271
Figure 8.15
Probability the network
will be completed in 22
weeks or less
Probability Analysis of the Project: Example 3

28. 28
Project Crashing and Time-Cost Trade-Off: Definition
• Project duration can be reduced by assigning more resources to project activities.
• Doing this however increases project cost.
• Decision is based on analysis of trade-off between time and cost.
• Project crashing is a method for shortening project duration by reducing one or
more critical activities to a time less than normal activity time.
• Crashing achieved by devoting more resources to crashed activities.

29. Chapter 8 - Project Management 29
Crashing Activity Times
• In the Critical Path Method (CPM) approach to project scheduling, it is
assumed that the normal time to complete an activity, tj , which can be
met at a normal cost, cj , can be crashed to a reduced time, tj’, under
maximum crashing for an increased cost, cj’.
• It is assumed that its cost per unit reduction, Kj , is linear and can be
calculated by:
Kj = (cj' - cj)/(tj - tj').
E.g.: in the example on the right,
Kj = total crash cost/total crash time
= $2000/5 = $400/wk

30. Chapter 8 - Project Management 30
Normal Crash
Activity Time Cost Time Cost
A) Study Feasibility 6 $ 80,000 5 $100,000
B) Purchase Building 4 100,000 4 100,000
C) Hire Project Leader 3 50,000 2 100,000
D) Select Advertising Staff 5 150,000 2 300,000
E) Purchase Materials 1 180,000 1 180,000
F) Hire Manufacturing Staff 4 300,000 1 480,000
G) Manufacture Prototype 2 100,000 2 100,000
H) Produce First 50 Units 6 450,000 5 800,000
I) Advertising Product 5 350,000 1 650,000
J) Assessing User Feedback 3 300,000 3 300,000
K) Distributing Product 5 550,000 5 550,000
 Normal Costs and Crash Costs
Crashing Example for Riverwalk Associates

31. Chapter 8 - Project Management 31
Crashing: The completion time for this project using normal times is 23
weeks. Which activities should be crashed, and by how many weeks, in
order for the project to be completed in a Target of 20 weeks?
Let: Yi = the amount of time activity i is crashed.
Then borrow from the LP formulation for the Earliest Times, we have the
following…
Crashing Example

32. Chapter 8 - Project Management 32
Min 20YA + 50YC + 50YD + 60YF
+ 350YH + 75YI
S.t.
EF_A - ES_A >= 6 - YA
EF_B - ES_B >= 4
EF_C - ES_C >= 3 - YC
EF_D - ES_D >= 5 - YD
EF_E - ES_E >= 1
EF_F - ES_F >= 4 - YF
EF_G - ES_G >= 2
EF_H - ES_H >= 6 - YH
EF_I - ES_I >= 5 - YI
EF_J - ES_J >= 3
EF_K - ES_K >= 5
ES_C - EF_A >= 0 (Not “=“ )
ES_D - EF_A >= 0
ES_E - EF_A >= 0
LP Model for Crashing
ES_F - EF_B >= 0
ES_G - EF_B >= 0
ES_F - EF_C >= 0
ES_G - EF_C >= 0
ES_J - EF_D >= 0
ES_J - EF_H >= 0
ES_H - EF_E >= 0
ES_H - EF_F >= 0
ES_I - EF_E >= 0
ES_I - EF_F >= 0
ES_K - EF_G >= 0
ES_K - EF_I >= 0
FINISH - EF_J >= 0
FINISH - EF_K >= 0
FINISH <= 20 (Target)
YA <=1
YC <=1
YD <=3
YF <=3
YH <=1
YI <=4

33. Chapter 8 - Project Management 33
Project Crashing and Time-Cost Trade-Off
General Relationship of Time and Cost
• Project crashing costs and indirect costs have an inverse relationship.
• Crashing costs are highest when the project is shortened.
• Indirect costs increase as the project duration increases.
• Optimal project time is at minimum point on the total cost curve.
Figure 8.20
The time–cost trade-off