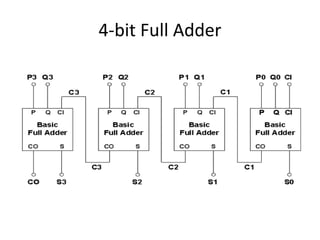
This document summarizes digital logic design lecture 4 on binary addition and signed numbers. It discusses: 1) The rules of binary addition and how to add 4-bit binary numbers using a full adder. 2) How signed numbers work in binary, including problems with the signed magnitude representation. 3) How two's complement solves the problems with signed magnitude by representing negative numbers as the binary equivalents of their positive value subtracted from 2^n. 4) Examples of adding and converting between positive and negative numbers using two's complement.

1. Digital Logic Design (DLD)
Lecture # 4
Prepared By
Tayyaba Altaf

2. Binary Addition

3. Rules
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (10, carry of one to the next bit)

4. Addition
• Take 4-bit values by adding 6 and 7.
• 1 1 carry
0110 6
0111 7 8 4 2 1
1101 13 1 1 0 1

5. One Bit Adder
a b Cin Cout S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1

6. 4-bit Full Adder

7. Signed Number
• Every Number can have both positive +5 and
negative -5 number. In binary number system
positive number can easily expressed.
• Take 4-bit, Normally 0 as a last bit represent
positive number (i.e. +5 = 0101)
• Make last bit 1 for negative number (i.e. -
5=1101)

8. Problem with Signed Number
With 3-bit magnitude, the range of numbers
available would be from +7 to -7.
Most computers use a larger number of bits to
store numbers.
The major problem with signed magnitude is
complexity of arithmetic.

9. Examples
Consider following problems with signed numbers.
+5 -5
+3 -3
+8 - 8
 -8 can not be represented in 4 bit signed
number.

10. 2’s Complement
Signed binary numbers are nearly always stored
in two’s complement format.
Leading bit is still the sign bit (0 for positive)
The largest number that can be stored is 2n-1 -1
(7 for n=4)
 The negative number –a is stored as the binary
equivalent of 2n – a in an n-bit system. E.g. -3 is
stored as the binary for 16-3 = 13, that is 1101.

11. 2’s Complement
• Convert 4-bit positive number into negative by
using two’s complement method is follow
+5 0101
For negative number, convert all 1’s into 0’s and
all 0’s into 1’s and add 1. above binary number
will become.
1010
+ 1
1011 -5

12. 2’s Complement
• Note that there is no negative zero; the process of
complementing +0 produces an answer 0000. In
two’s complement addition, the carry out of the
most significant bit is ignored.
• For Example: -0
0: 0000
1111
+ 1
0000

13. 2’s Complement
• For 4-bit numbers, that range is -8<=sum<=+7
• The reason that two’s complement is so
popular in the simplicity of addition.

14. Singed and unsigned 4-bit numbers.
Binary Positive Signed (2’s comp)
0000 0 0
0001 1 +1
0010 2 +2
0011 3 +3
0100 4 +4
0101 5 +5
0110 6 +6
0111 7 +7
1000 8 -8
1001 9 -7
1010 10 -6
1011 11 -5
1100 12 -4
1101 13 -3
1110 14 -2
1111 15 -1

15. Class Task
• Solve following operation.
i) 5-7
ii) 7- (-5)
iii) -5 +3