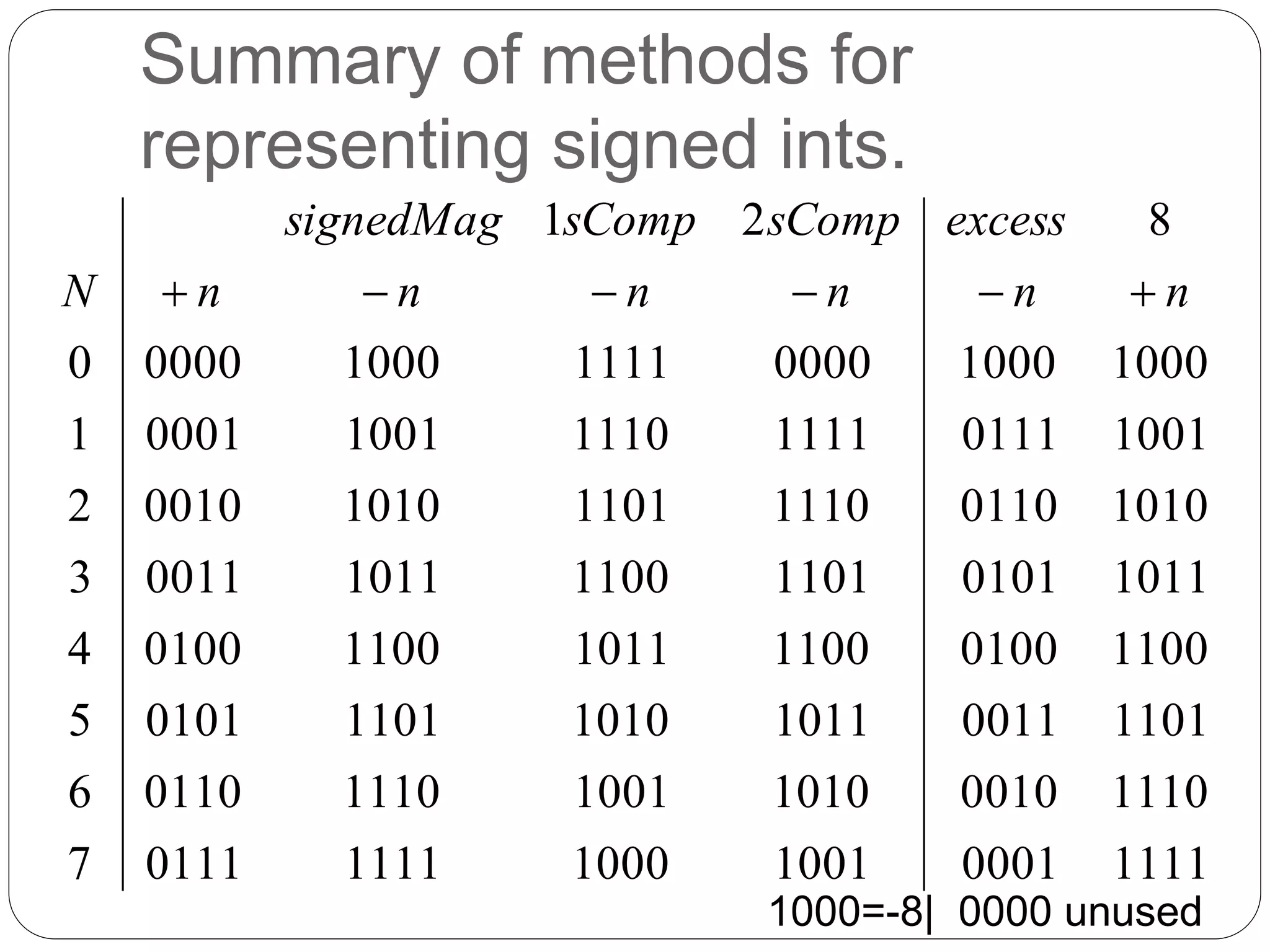
The document discusses binary numbers and arithmetic. It covers topics like addition, subtraction, multiplication in binary, and different methods for representing signed integers like two's complement. It explains how two's complement works by using bitwise operations to represent negative numbers. For example, it shows that adding two positive 8-bit binary numbers in two's complement is simply the bitwise addition, while subtraction can be performed by adding the number and the two's complement of the subtrahend. The document also discusses issues like carry vs overflow that can occur during binary arithmetic operations.













![Representing numbers (ints)
Fixed, finite number of bits.
bits bytes C/C++ Intel Sun
8 1 char [s]byte byte
16 2 short [s]word half
32 4 int or long [s]dword word
64 8 long long [s]qword xword](https://image.slidesharecdn.com/mbaadmissioninindia-140909020154-phpapp02/75/Mba-admission-in-india-14-2048.jpg)
![Representing numbers (ints)
Fixed, finite number of bits.
bits Intel signed unsigned
8 [s]byte -27..+27-1 0..+28-1
16 [s]word -215..+215-1 0..+216-1
32 [s]dword -231..+231-1 0..+232-1
64 [s]qword -263..+263-1 0..+264-1
In general, for k bits, the unsigned range is [0..+2k-1] and
the signed range is [-2k-1..+2k-1-1].](https://image.slidesharecdn.com/mbaadmissioninindia-140909020154-phpapp02/75/Mba-admission-in-india-15-2048.jpg)

















![Representing numbers (ints)
using 2’s complement
Fixed, finite number of bits.
bits Intel signed
8 sbyte -27..+27-1
16 sword -215..+215-1
32 sdword -231..+231-1
64 sqword -263..+263-1
In general, for k bits, the signed range is [-2k-1..+2k-1-1].
So where does the extra negative value come from?](https://image.slidesharecdn.com/mbaadmissioninindia-140909020154-phpapp02/75/Mba-admission-in-india-34-2048.jpg)
![Representing numbers (ints)
Fixed, finite number of bits.
bits Intel signed
8 sbyte -27..+27-1
16 sword -215..+215-1
32 sdword -231..+231-1
64 sqword -263..+263-1
In general, for k bits, the signed range
is
[-2k-1..+2k-1-1].
So where does the extra negative value
come from?
n n
0 0000 0000
1 0001 1111
2 0010 1110
3 0011 1101
4 0100 1100
5 0101 1011
6 0110 1010
7 0111 1001
8 1000](https://image.slidesharecdn.com/mbaadmissioninindia-140909020154-phpapp02/75/Mba-admission-in-india-35-2048.jpg)






![Addition of 2’s complement
binary numbers
class test {
public static void main ( String
args[] )
{
byte A = 127;
byte B = 127;
byte result = (byte)(A + B);
System.out.println( "A + B = "
+ result );
}
}
#include <stdio.h>
int main ( int argc, char* argv[] )
{
char A = 127;
char B = 127;
char result = (char)(A + B);
printf( "A + B = %d n", result );
return 0;
} Result = -2 in both
Java (left) and C++
(right). Why?](https://image.slidesharecdn.com/mbaadmissioninindia-140909020154-phpapp02/75/Mba-admission-in-india-42-2048.jpg)
![Addition of 2’s complement
binary numbers
class test {
public static void main ( String
args[] )
{
byte A = 127;
byte B = 127;
byte result = (byte)(A + B);
System.out.println( "A + B = "
+ result );
}
}
Result = -2 in both Java and
C++.
Why?
What’s 127 as a 2’s
complement binary number?
01111111
01111111
11111110
What is 111111102?
Flip the bits: 00000001.
Then add 1: 00000010.](https://image.slidesharecdn.com/mbaadmissioninindia-140909020154-phpapp02/75/Mba-admission-in-india-43-2048.jpg)







