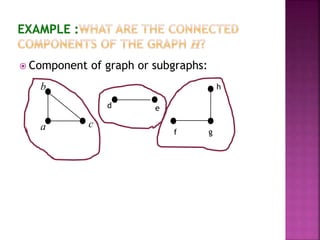
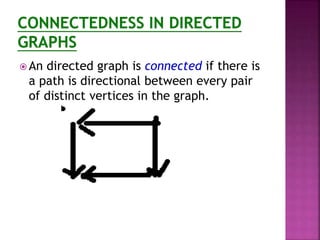
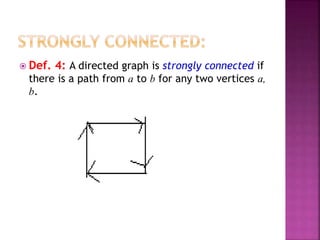
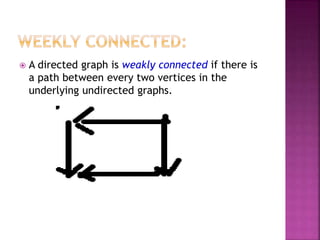
The document discusses various concepts related to connectivity in graphs. It defines what makes a graph connected versus disconnected. Key points include: a connected graph has a path between all vertex pairs; removing vertices or edges can disconnect a graph; connected components are maximal connected subgraphs; cut vertices and edges disconnect the graph when removed. Graph isomorphism is also discussed, where two graphs are isomorphic if their adjacency matrices are identical.

1.  The word "connectivity" may refer to the
several meanings in day to day life.
Generally, it may refer to the connection
between two or more things or virtues

2.  A connected graph is an undirected graph
that has a path between every pair of
vertices

3.  A connected graph with at least 3 vertices is
1-connected if the removal of 1 vertex
disconnects the graph

5.  A bi-connected graph is a connected graph in
which there exist two vertices for which
there are two disjoint paths between these
two vertices.

6.  The connected graph is said to be
a undirected graph which has at least one
path between each pair of vertices.

7.  A graph is connected when there is a path
between every pair of vertices. In a
connected graph, there are
no unreachable vertices. A graph that is not
connected is disconnected.
 A graph G is said to be disconnected if there
exist two nodes in G such that no path in G
has those nodes as endpoints.

A graph with just one vertex is connected.
An edgeless graph with two or more vertices
is disconnected.

8.  In the area of information and technology,
the connectivity may refer to internet
connectivity by which various individual
computers, cell phones and LANs can be
connected to global Internet.

9.  In mathematics and computer
science, connectivity is one of the basic
concepts of graph theory: It is closely related
to the theory of network flow problems. The
connectivity of a graph is an important
measure of its resilience as a network.

10. An undirected graph is connected if
there is a path between every pair of
distinct vertices in the graph.
Connected component:
 maximal connected subgraph. (An
unconnected graph will have several
component)

11.  Component of graph or subgraphs:
a
b
c
d e
f g
h

12. A cut vertex separates one connected
component into several components if it is
removed.
OR
Cut vertices are vertices that produce a
subgraph with more connected components
when removed from a graph (and all incident
edges to it). Removing a cut vertex v in in a
connected graph G will make G disconnected.

13. A cut edge separates one connected
component into two components if it is
removed
OR
Cut edges or bridges are edges that
produce a subgraph with more connected
components when removed from a graph.
Removing a cut edge (u; v) in a connected
graph G will make G disconnected

14. .Find the cut vertices and cut edges in the
graph G.
Sol:
cut edges: cut vertices:
{a, b}, {c, e} b, c, e
b
a
c
d
e h
gf
G

15.  An directed graph is connected if there is
a path is directional between every pair
of distinct vertices in the graph.

16.  Def. 4: A directed graph is strongly connected if
there is a path from a to b for any two vertices a,
b.

17.  A directed graph is weakly connected if there is
a path between every two vertices in the
underlying undirected graphs.

18.  Definition:
 , G1 and G2 are isomorphic if their vertices can
be ordered in such a way that the adjacency
matrices MG1
and MG2
are identical.
 Function of isomorphic graph like f(G) is called
an isomorphism.

19.  Properties that two isomorphic simple graphs
must both have they must have :
• the same number of vertices,
• the same number of edges, and
• the same degrees of vertices.

20. Def.
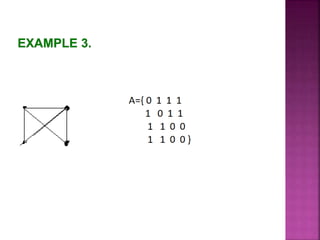
G=(V, E) : simple graph, V={v1,v2,…,vn}. (Order doesn't matter)
A matrix A is called the adjacency matrix of G
if A=[aij]nn , where aij = 1, if {vi,vj}E,
0, otherwise.