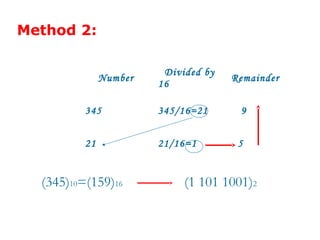
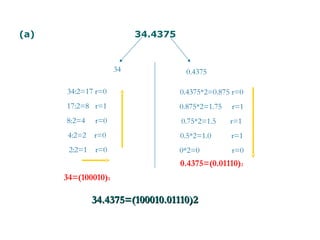
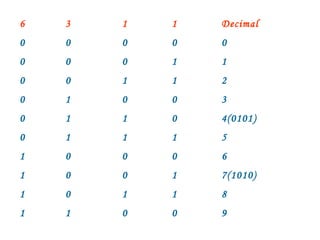
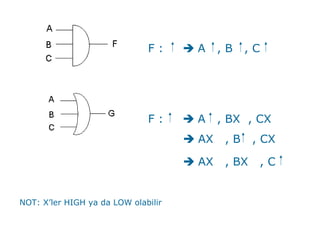
This document contains examples and problems related to binary number systems. It begins by listing octal, hexadecimal, and base-12 numbers and converting between number systems. Later problems involve operations like addition, subtraction, multiplication and division using binary, octal and hexadecimal numbers. Conversions between decimal, binary, octal and hexadecimal are demonstrated. Complement representations for signed binary numbers are also covered.

1. DIGITAL DESIGN
THIRD EDITION
M. MORRIS MANO
CHAPTER 1 : BINARY
SYSTEMS PROBLEMS

2. 1.1-) List the octal and the hexadecimal numbers
from 16 to 32. Using A and B for the last two
digits, list the numbers from 10 to 26 in base 12 .
Octal :
16 = 8¹ x 2 + 8º x 0 => (16)10 = (20)8
32 = 8¹ x 4 + 8º x 0 => (32)10 = (40)8
20, 21, 22, 23, 24, 25, 26, 27, 30, 31, 32, 33, 34, 35, 36, 37, 40

3. Hexadecimal :
16 = 16¹ x 1 + 16º x 0 => (16)10 = (10)16
32 = 16¹ x 2 + 16º x 0 => (32)10 = (20)8
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B , 1C, 1D, 1E, 1F, 20
Base-12 :
10 = 12º x A => (10)10 = (A)12
26 = 12¹ x 2 + 12º x 2 => (26)10 = (22)12
A, B, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 20, 21, 22

4. 1.2-) What is the exact number of bytes in a
system that contains (a) 32K byte, (b)64M bytes,
and (c)6.4G byte ?
(a) 32K byte:
1K = 2¹º = 1,024
32K = 32 x 2¹º = 32 x 1,024 = 32,768
32K byte = 32,768 byte

5. (b) 64M byte:
1M = 2²º = 1,048,576
64M = 64 x 2²º = 64 x 1,048,576 = 67,108,864
64M byte = 67,108,864 byte
(c) 6.4G byte:
1G = 2³º = 1,073,741,824
6.4G = 6.4 x 2³º = 6.4 x 1,073,741,824 = 6,871,747,674
6.4G byte = 6,871,747,674 byte

6. 1.3-) What is the largest binary number that can
be expressed with 12 bits? What is the equivalent
decimal and hexadecimal ?
Binary:
(111111111111)2
Decimal:
(111111111111)2 = 1x 2º+ 1 x 2¹ + 1 x 2² +…..+ 1 x 2¹¹ + 1 x 2¹²
(111111111111)2 = 4,095
Hexadecimal:
(1111 1111 1111)2 = (FFF)16
F F F

7. 1.4-) Convert the following numbers with the
indicated bases to decimal : (4310)5 , and
(198)12 .
(4310)5 = 0 x 5º + 1 x 5¹ + 3 x 5² + 4 x 5³ = 0 + 5 + 75 + 500
(4310)5 = 580
(198)12 = 8 x 12º + 9 x 12¹ + 1 x 12² = 8 + 108 + 144
(198)12 = 260

8. 1.5-) Determine the base of the numbers in each
case for the following operations to be correct :
(a) 14/2 = 5 ; (b) 54/4 = 13 ; (c) 24+17 = 40 .
(a) (14)a / (2)a = (5)a ⇒ (4 x aº + 1 x a¹) / (2 x aº) = 5 x aº
⇒ (4 + a) / 2 = 5
⇒ 4 + a = 10
⇒a=6

9. (b) (54)b / (4)b = (13)b ⇒ (4 x bº + 5 x b¹) / (4 x bº) = 3 x bº + 1 x b¹
⇒ (4 + 5b) / 4 = 3 + b
⇒ 4 + 5b = 12 + 4b
⇒b=8
(c) (24)c + (17)c = (40)c ⇒ (4 x cº + 2 x c¹) + (7 x cº + 1 x c¹) = 4 x c¹
⇒ 4 + 2c + 7 + c = 4c
⇒ c = 11

10. 1.6-) The solution to the quadratic equation x² -
11x + 22 = 0 is x=3 and x=6. What is the base
of the numbers?
x² - 11x + 22 = (x – 3) . (x – 6)
x² - 11x + 22 = x² - (6 + 3)x + (6.3)
⇒ (11)a = (6)a + (3)a
⇒1+a=6+3
⇒a=8

11. 1.7-) Express the following numbers in decimal :
(10110.0101)2 , (16.5)16 , (26.24)8 .
( 1 0 1 1 0 . 0 1 0 1 )2 = 2¹ + 2² + (2^4) +( 2^-2) + (2^-4)
4 3 2 1 0 -1 -2 -3 -4
(10110.0101)2 = 2 + 4 + 16 + (1/4) + (1/16)
(10110.0101)2 = 22.3125

12. ( 1 6 . 5 )16 = 6 x 16º + 1 x 16¹ + 5 x (16^-1)
1 0 -1
(16.5)16 = 6 + 16 + (5/16)
(16.5)16 = 22.3125
( 2 6 . 2 4 )8 = 6 x 8º + 2 x 8¹ + 2 x (8^-1) + 4 x (8^-2)
1 0 -1 -2
(26.24)8 = 6 + 16 + (2/8) + (4/64)
(26.24)8 = 22.3125

13. 1.8-) Convert the following binary numbers to
hexadecimal and to decimal : (a) 1.11010 , (b)
1110.10 . Explain why the decimal answer in (b)
is 8 times that of (a) .
(a) ( 1 . 1101 0 )2 = ( 1 . D )16 = 1 x 16º + D x (16^-1)
1 D 0 0 -1

14. 1.9-) Convert the hexadecimal number 68BE to
binary and then from binary convert it to octal .
(68BE) 16
Binary form:
(0110 1000 1011 1110)2=(0110100010111110)2
6 8 B E
Octal form:
(0 110 100 010 111 110)2
0 6 4 2 7 6 =(064276)8

15. (a) 1.10-) Convert the decimal number 345 to
binary in two ways :
Convert directly to binary;
Convert first to hexadecimal, then from
hexadecimal to binary. Which method is
faster ?

16. Method 1:
Number Divided by 2 Remainder
(345)10 345 345/2=172 1
172 172/2=86 0
86 86/2=43 0
43 43/2=21 1
21 21/2=10 1
10 10/2=5 0
5 5/2=2 1
2 2/2=1 1

17. Method 2:
Divided by
Number Remainder
16
345 345/16=21 9
21 21/16=1 5
(345)10=(159)16 (1 101 1001)2

18. 1.11-) Do the following conversion problems :
(a) Convert decimal 34.4375 to binary .
(b) Calculate the binary equivalent of 1/3
out to 8 places.
Then convert from binary to decimal. How
close is the
result to 1/3 ?
(c) Convert the binary result in (b) into
hexadecimal. Then
convert the result to decimal . Is the answer
the same ?

19. (a) 34.4375
34 0.4375
34:2=17 r=0 0.4375*2=0.875 r=0
17:2=8 r=1 0.875*2=1.75 r=1
8:2=4 r=0 0.75*2=1.5 r=1
4:2=2 r=0 0.5*2=1.0 r=1
2:2=1 r=0 0*2=0 r=0
0.4375=(0.01110)2
34=(100010)2
34.4375=(100010.01110)2

20. (b) 1/3=0.3333…
0.33333*2=0.66666 r=0
0.66666*2=1.33332 r=1
0.33332*2=0.66664 r=0
0.66664*2=1.33328 r=1
.
.
.
0.3333…=(0.010101….)= 0+ ¼ + 0 +
1/8 + 0 + 1/32 +… =~0.33333…

21. (c)
0.010101010…=0.0101 0101
0101
(0.555..)16=5/16 +5/256 +5/4096 +…=~0.33203

22. 1.12-) Add and multiply the following numbers
without
converting them to decimal.
(a) Binary numbers 1011 and 101 .
(b) Hexadecimal numbers 2E and 34 .
(a) 1011 (11) 1011(11)
101 (5) 101(5)
+__________ x_____
10000(16) 1011
0000
+ 1011
_________
110111 (55)

23. (b)
2E (46) 2E
34 (52) 34
+____ x____
62 (98) B8
8A
+____
958(2392)

24. 1.13-) Perform the following division in binary :
1011111 ÷ 101 .
(1011111)2=95
(101)2=5
95/5=19 (10011)2
1011111 101
101 10011
000111
101
0101
101
0000

25. 1.14-) Find the 9’s- and the 10’s-complement of
the following decimal numbers :
(a) 98127634 (b) 72049900 (c) 10000000 (d)
00000000 .
9’s comlements :
(a) 99999999-98127634=01872365
(b) 99999999-72049900=27950099
(c) 99999999-10000000=89999999
(d) 99999999-0000000=99999999

26. 10’s complements
(a)100000000- 98127634= 01872366
(b)100000000-72049900=27950100
(c)100000000-10000000=90000000
(d)100000000-0000000=00000000

27. 1.15-) (a) Find the 16’s-complement of AF3B .
(b) Convert AF3B to binary .
(c) Find the 2’s-complement of the result in (b)
(d) Convert the answer in (c) to hexadecimal and
compare with the answer in (a)
(a)16^5-AF3B=50C5
(b)(AF3B)16=1010 1111 0011 1011
(c)1010111100111011
0101000011000101
(d)0101 0000 1100 0101= 50C5

28. 1.16-) Obtain the 1’s and 2’S complements of the
following binary numbers :
(a)11101010 (b)01111110 (c)00000001
(d)10000000 (e)00000000
1’s complements:
(a) 00010101 (b)10000001 (c)11111110 (d)01111111
(e)11111111
2’s complement :
(a) 00010110 (b)10000010 (c)11111111 (d)10000000
(e)00000000

29. 1.17-) Perform subtraction on the following
unsigned numbers using the 2’s-complement of
the subtrahend. Where the result shoud be
negative, 10’s complement it and affix a minus
sign. Verify your answers .
(a) 7188-3049 (b)150-2100 (c)2997-7992
(d)1321-375

30. (a)7188+6951=4139 One carry out so
answer is correct.
(b)150+7900=8050 correct answer=-1950
(c)2997+2008=5005 correct answer=-4995
(d)1321+9625=0946 One carry out so
answer is correct.

31. 1.18-) Perform subtraction on the following
unsigned binary numbers using the 2’s-
complement of the subtrahend. Where the result
should be negative, 2’s complement it and affix a
minus sign .
(a)11011-11001 (b)110100-10101 (c)1011-
110000 (d)101010-101011

32. (a)11011+00111=00010(27-25=2)
(b)110100+01011=011111(52-21=31)
(c)1011+010000=011011 -100101(11-48=-37)
(d)101010+010101=111111-000001(42-43=-1)

33. 1.19-) The following decimal numbers are shown
in sign- magnitude form : +9826 and +801.
Convert them to signed 10’s-complement form
and perform the following operations : (Note that
the sum is +10627 and requires six digits).
(a) (+9826)+(+801) (b)(+9826)+(-801)
(c)(-9826)+(+801) (d)(-9826)+(-801)

34. (a)009826+00801=010627
(b)009826+999199=09025
(c)990174+000801=990975 -09025
(d)990174+999199=989373 -10627

35. 1.20-) Convert decimal +61 and +27 to binary
using the signed-2’s complement representation
and enough digits to accomodate the numbers.
Then perform the binary equivalent of (+27) + (-
61) , (- 27) + (+61) and (-27) + (- 61) .
Convert the answers back to ecimal and verify that
they are correct .

36. +61=0111101 -61=1000011
+27=0011011 -27=1100101
(a)27+(-61)=0011011+1000011=1011110
(b)-27+(+61)=1100101+0111101=0100010
(c)-27+(-61)=
1100101+1000011=0101000(overflow)
11100101+11000011=10101000

37. 1.21-) Convert decimal 9126 to both BCD and
ASCII codes. For ASCII, an odd parity bit is to be
appended at the left .
BCD: 1001 0001 0010 0110
ASCII: 10111001 00110001 00110010 10110110

38. 1.22-) Represent the unsigned decimal numbers
965 and 672 in BCD and then show the steps
necessary to form their sum .
965= 1001 0110 0101
672= 0110 0111 0010
+___ ___ ____
1 0000 1101 0111
+0110 +0110
+_________________
0001 0110 0011 0111  (1637)10

39. 1.23-) Formulate a weighted binary code for the
decimal digits using weights 6, 3, 1, 1 .

40. 6 3 1 1 Decimal
0 0 0 0 0
0 0 0 1 1
0 0 1 1 2
0 1 0 0 3
0 1 1 0 4(0101)
0 1 1 1 5
1 0 0 0 6
1 0 0 1 7(1010)
1 0 1 1 8
1 1 0 0 9

41. 1.24-) Represent decimal number 6027 in
(a) BCD, (b) excess-3 code, and (c)
2421 code .
(a)6027 BCD : 0110 0000 0010 0111
(b)excess3: 1001 0011 0101 1010
(c)(c)0110 0000 0010 1101

42. 1.25-) Find the 9’s complement of 6027 and
express it in 2421 code. Show that the result is
the 1’s complement of the answer to (c) in
Problem 1.24 . This demonstrates that the 2421
code is self-complementing .
9’s complement of 6027 is 3972
6027 as 2421 code is  0110 0000 0010 1101
3972 as 2421 code is 0011 1111 1101 0010

43. 1.26-) Assign a binary code in some orderly
manner to the 51 playing cards. Use the
minimum number of bits.
2^4 =16
2^5 =32
2^6=64  6 bits are necessary.

44. 1.27-) Write the expresion “G. Boole” in ASCII
using an eight-bit code. Include the period and
the space. Treat the leftmost bit of each character
as a parity bit. Each 8-bit code shouls have even
parity.
G . B O O L E
(01000111)(00101110) (01000010) (01101111) (01101111) (01101100) (01100101)

45. 1.28-) Decode the following ASCII code : 1001010
1100001
1101110 1100101 0100000 1000100 1101111
1100101 .
Jane
Doe

46. 1.29-) The following is a string of ASCII
characters whose bit patterns have benn
converted into hexadecimal for compactness : 4A
EF 68 6E 20 C4 EF E5 . Of the 8 bits in each
pair of digits, the leftmost is a parity bit. The
remaining bits are the ASCII code.
01001010 11101111 01101000 01101110 00100000 11000100 11101111 11100101
J O H N (space) D O E

47. 1.30-) How many printing characters are there in
ASCII ?
How many of them are special characters (not
letters or numerals) ?
94 characters
62 of them are numbers and letters.
32 of them are special characters.

48. 1.31-) What bit must be complemented to change
an ASCII letter from capital to lowercase, and
vice versa ?
Cevap: Bir ASCII karakteri büyük harften küçük harfe
çevirmek için sağdan 6. bit 0 iken 1 yapılır. Küçükten
büyüğe çevrilecekse 1 iken 0 yapılır.

49. 1.32-) The state of a 12-bit register is
100010010111 . What is its content if it
represents
(a) three decimal digits in BCD?
(b) three decimal digits in the excess-3 code?
(c) three decimal digits in 84-2-1 code?
(d) binary number?

50. Three Decimal Digits in BCD:
1000 1001 0111 897
Three Decimal Digits in Exces-3 Code:
1000 1001 0111 564
(8-3) (9-3) (7-3)
Three Decimal Digits in the 8-4-2-1 Code:
1000 1001 0111 897
8 9 7
Binary Code:
100010010111 2^11+2^7+2^4+2^2+2+1=2199

51. 1.33-) List the ASCII code for the 10 decimal
digits with an even parity bit in the leftmos
position.
00110000
10110001
10110010
00110011
10110100
00110101
00110110
10110111
10111000
00111001

52. 1.34-) Assume a 3-input AND gate with output F
and a 3-input OR gate with output G. Inputs are
A, B, and C . Show the signals (by means of a
timing diagram) of the outputs F and G as
functions of three inputs ABC. Use all possible
combinations of ABC.

53. F: A ,B ,C
F: A , BX , CX
 AX ,B , CX
 AX , BX ,C
NOT: X’ler HIGH ya da LOW olabilir