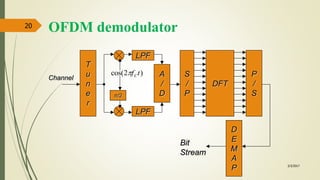
The document discusses Orthogonal Frequency Division Multiplexing (OFDM), its principles, and applications in technologies such as ADSL and digital broadcasting. It explains the process of spreading transmitted data over multiple orthogonal carriers, the necessity of cyclic prefix insertion to mitigate interference, and the application of Fast Fourier Transform (FFT) for signal processing. Details are provided on the implementation of OFDM systems, including challenges related to intersymbol and inter-carrier interference.

1. OFDM
ORTHOGONAL FREQUENCY DIVIDION MULTIPLEXING
Submitted to-
Mr. Hemant Kumar Meena
Assistant Professor
Electrical Engineering Department
Submitted by-
 Toshim Kumar (2013UEE1593)
 Manish Gupta (2013UEE1762)
 Bankesh Mehta (2013UEE1614)
 Khinya Ram (2013UEE1597)

2. OFDM was invented more than 40 years.
OFDM has been adopted for several technologies.
Asymmetric Digital Subscriber Line(ADSL) services.
Digital Audio broadcast(DAB).
Digital Terrestrial television broadcast.
History of OFDM

3. Principle of OFDM
 Data to be transmitted is spreaded over a large number of carriers.
 Each carrier modulated at a low rate.
 Carriers are orthogonal to each other.
 Divides the total available bandwidth in the spectrum into sub-bands for multiple
carriers to transmit in parallel.
 Combines a large number of low data rate carriers to construct a composite high
data rate communication system.

4. ORTHOGONALITY
 Two conditions must be considered for the orthogonality between the subcarriers.
Each subcarrier has exactly an integer number of cycles in the FFT interval.
The number of cycles between adjacent subcarriers differs by exactly one.

5. Orthogonality
Time domain Frequency domain
Example of four subcarriers within one OFDM symbol Spectra of individual subcarriers

7. FFT Based ofdm system

8. OFDM Implementation
Signal
Mapper
(QPSK)
IFFT
Parallel-
to-Serial
Converter
Guard
Interval
Insertion
Serial-to-
Parallel
Converter
2d
1nd 
Serial
Data
Input
1s
2s
1ns 
x bits
D/A
&
Lowpass
Filter
1x 1d
2x
1nx 
x= [1,0,1,1,0,0…] x1=[1,0]
x2=[1,1]
x3=[0,0]
……..
d1=[-1]
d2=[-i]
d3=[1]
……..

9. IMPLEMENTATION
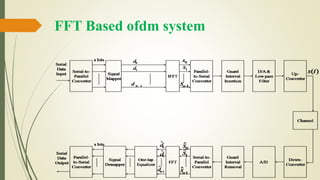
 Discrete Fourier transform (DFT) and inverse DFT (IDFT) processes are useful for implementing
these orthogonal signals.
 Note that DFT and IDFT can be implemented efficiently by using fast Fourier transform (FFT)
and inverse fast Fourier transform (IFFT), respectively.
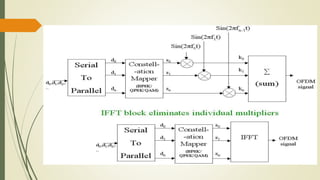
 In the OFDM transmission system, N-point IFFT is taken for the transmitted symbols
so as to generate , the samples for the sum of N orthogonal subcarrier signals.
 Let y[n] denote the received sample that corresponds to x[n] with the additive noise w[n] (i.e.,
y[n] =x[n]+w[n]).
 Taking the N-point FFT of the received samples, , the noisy version of transmitted
symbols
can be obtained in the receiver.

11. Cyclic Prefix Insertion
 Because wireless communications systems are susceptible to multi-path channel reflections, a
cyclic prefix is added to reduce ISI. A cyclic prefix is a repetition of the first section of a
symbol that is appended to the end of the symbol. In addition, it is important because it enables
multi-path representations of the original signal to fade so that they do not interfere with the
subsequent symbol.

12. Guard Interval and Cyclic Extension
 Two different sources of interference can be identified in the OFDM system.
 Intersymbol interference (ISI) is defined as the crosstalk between signals
within the same sub-channel of consecutive FFT frames, which are separated
in time by the signaling interval T.
 Inter-carrier interference (ICI) is the crosstalk between adjacent subchannels
or frequency bands of the same FFT frame.

13. Guard Interval and Cyclic Extension
 For the purpose to eliminate the effect of ISI, the guard interval could consist of no signals at all.
 Guard interval (or cyclic extension) is used in OFDM systems to combat against multipath fading.
Tg :guard interval
Tdelay-spread : multi path delay spread
Tg > Tdelay-spread
 In that case, however, the problem of inter-carrier interference (ICI) would arise.
 The reason is that there is no integer number of cycles difference between subcarriers within the
FFT interval.

14. Guard Interval and Cyclic Extension
 Delay spread
Environment Delay Spread
Home < 50 ns
Office ~ 100 ns
Manufactures 200 ~ 300 ns
Suburban < 10 us

15. Guard Interval and Cyclic Extension
If T g < Tdely-spread
Tg Symbol 1 Tg Symbol 2 Tg Symbol 3 Tg Symbol 4
Tdely-spread
If Tg > Tdely-spread
Tg Symbol 1 Tg Symbol 2 Tg Symbol 3
Tg Symbol 1 Tg Symbol 2 Tg Symbol 3 Tg Symbol 4
Tg Symbol 1 Tg Symbol 2 Tg Symbol 3
Tdely-spread
﹒﹒﹒﹒
﹒﹒﹒﹒
﹒﹒﹒﹒
﹒﹒﹒﹒

16. Guard Interval and Cyclic Extension
 To eliminate ICI, the OFDM symbol is cyclically extended in the guard interval.
 This ensures that delayed replicas of the OFDM symbol always have an integer number of
cycles within the FFT interval, as long as the delay is smaller than the guard interval.
Guard Interval
(Cyclic Extension)

17. OFDM signal generation
3/3/2017
17
    s t a f nf t b f nf tn c n c
n
N
( ) cos ( ) sin ( )   


 2 20 0
0
1
 

18. OFDM signal generation in digital domain
Define complex base-band signal u(t) as follows
Perform N times sampling in period T
18
 s t u t
u t d e d a jb
B
n
j nf t
n
N
n n n
( ) Re ( )
( ) ,

   


 2
0
1
0
)1,,2,1,0(
1
0
2
1
0
21
0
2
0
0
0























Nked
eded
Nf
k
u
N
n
nk
N
j
n
N
n
N
nk
j
n
N
n
Nf
k
nfj
n
@@


u(k) = IFFT (dn) = IFFT(an + jbn)

19. OFDM modulator
3/3/2017
19
M
A
P
S
/
P
I-DFT
P
/
S
Real
cos( )2f tC
ＢＰＦAIR
Bit
stream
Imag
sin( )2f tC

20. OFDM demodulator
3/3/2017
20
T
u
n
e
r
S
/
P
DFT
P
/
S
A
/
D
LPF
Channel
cos( )2f tC
π/2
LPF
D
E
M
A
P
Bit
Stream

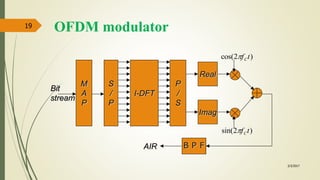
21. OFDM demodulation
3/3/2017
21
    
  )(
2
1
)2sin()2cos(
2
1
)]2cos()([
)(2sin)(2cos)(
1
0
00
1
0
00
tstnfbtnfatftsLPF
tnffbtnffats
I
N
n
nnC
N
n
cncn










    )(
2
1
)2cos()2sin(
2
1
])2sin()([
1
0
00 tstnfbtnfatftsLPF Q
N
n
nnC  



u t s t js t d eI Q n
j nf t
n
N
( ) ( ) ( )   


 2
0
1
0
dn = FFT(u(k))