Introduction to OFDM

Introduction to OFDM
Jay Chang
1

2
Single-Carrier vs. Multi-Carrier Transmission
Basic Principle of OFDM
Coded OFDM
OFDMA: Multiple Access Extensions of OFDM
Duplexing
Agenda

3
Coded OFDM
Duplexing
Agenda

4
Single-Carrier Baseband Transmission: System Model
Fig. Single-carrier baseband communication system model
where z(t) is an additive noise and g(t) is the impulse response of overall end-to-end system given as
The equalizer is designed to compensate the effect of channel.
When the noise term is ignored, the sampled output signal of the equalizer can be expressed as:
Isolating the nth sample to detect an:

5
Fig. Illustration: inter-symbol interference (ISI) and symbol period.
ISI
As illustrated here, the extent of ISI depends on the duration of a symbol period T: the shorter the symbol
period is, the larger the influence of the ISI may become.
ISI becomes significant as the data rate (R = 1/T) increases (i.e., decreasing T in Fig.) in a single-carrier system.

6
ISI and Nyquist Criterion
ISI can be completely eliminated by fulfilling the following time-domain condition on the overall impulse response:
equivalent
Nyquist filter is an ideal LPF, which has a sinc function-type of impulse response or equivalently, rectangular pulse (or brick-wall)
type of frequency response as described by
Where W = R/2 = 1/(2T). R and W correspond to the Nyquist rate and Nyquist bandwidth, respectively.
Note that the Nyquist bandwidth W is the minimum possible bandwidth that is required to realize the date rate R without ISI.
Another well-known physically realizable Nyquist filter is the raised-cosine filter, which frequency response:
Ideal filter is not physically realizable.
where r is the roll-off factor, 0 ≤ r ≤ 1.
( ) 2 2 2
sin / cos /
/ 1 4 /
S S
RC
S S
t T t T
h t
t T t T
π απ
π α
= ⋅
−
https://gist.github.com/oklachumi/1359d9a4acb697c21b93c5bfb147cb6a

7https://gist.github.com/oklachumi/96eccbf09ce5bdbb2a857e573e471bb5

9
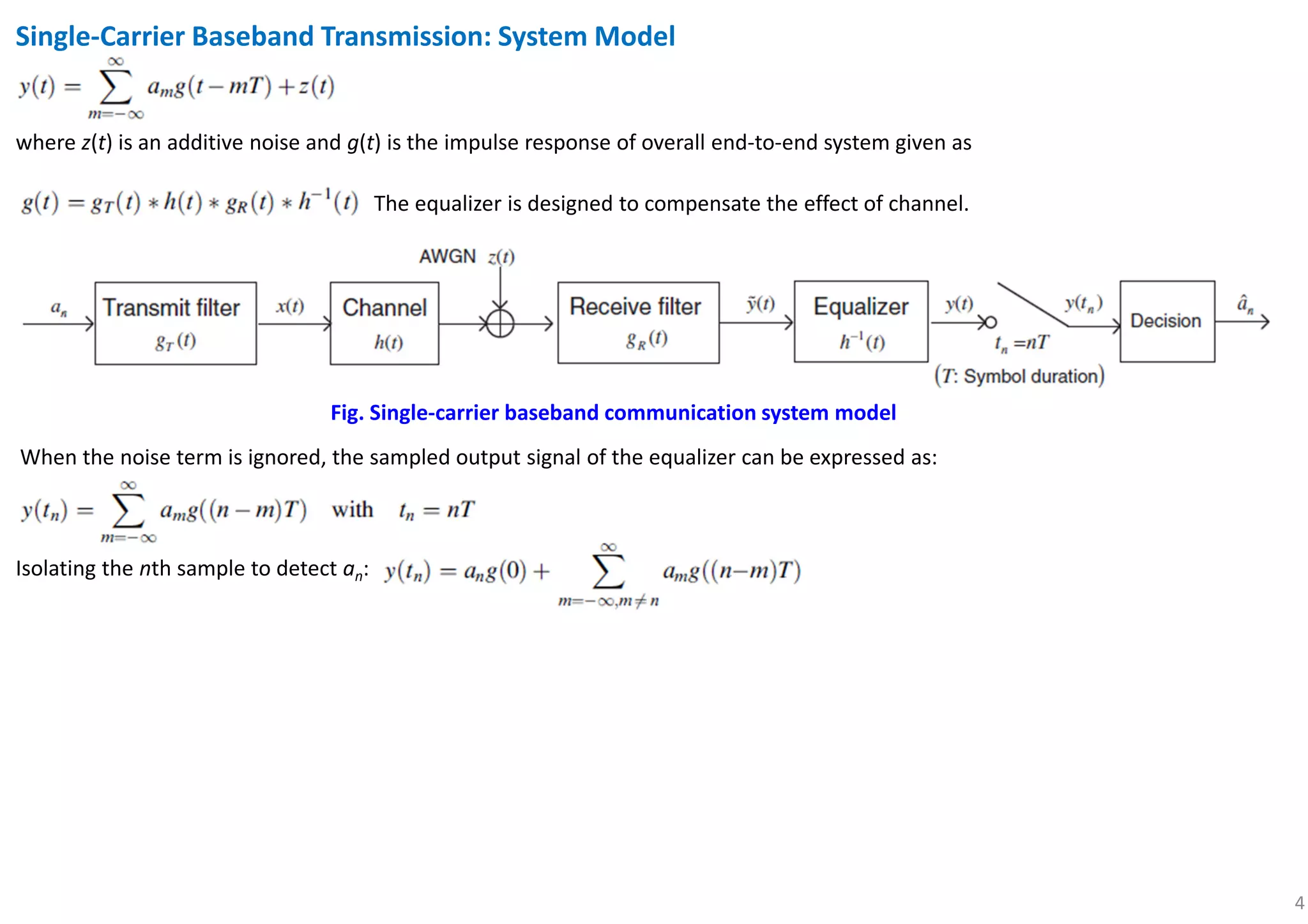
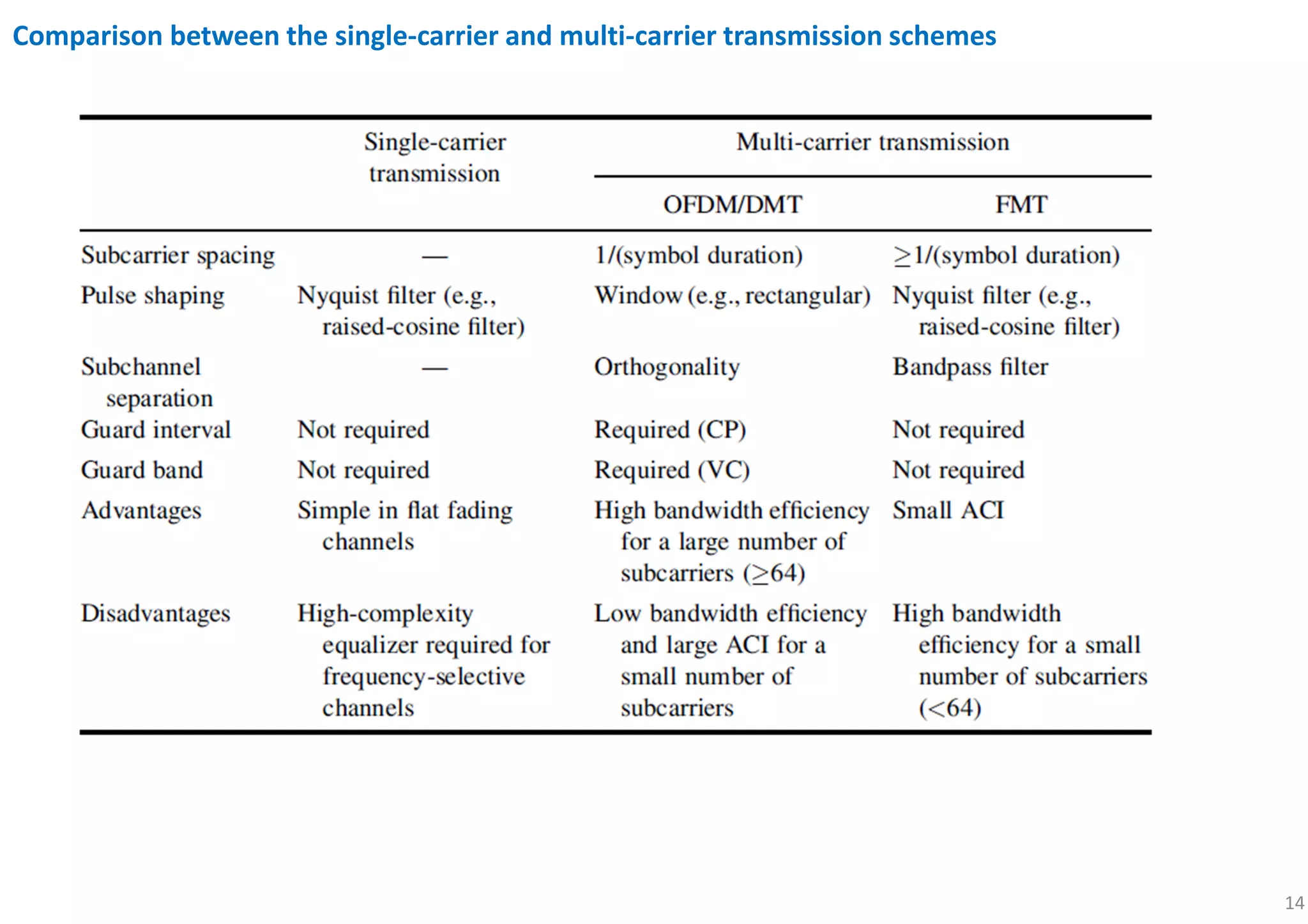
Limitation of Single-Carrier Transmission for High Data Rate
In order to support the symbol rate of Rs symbols per second, the minimum required bandwidth is the Nyquist bandwidth, BW =
Rs/2 [Hz].
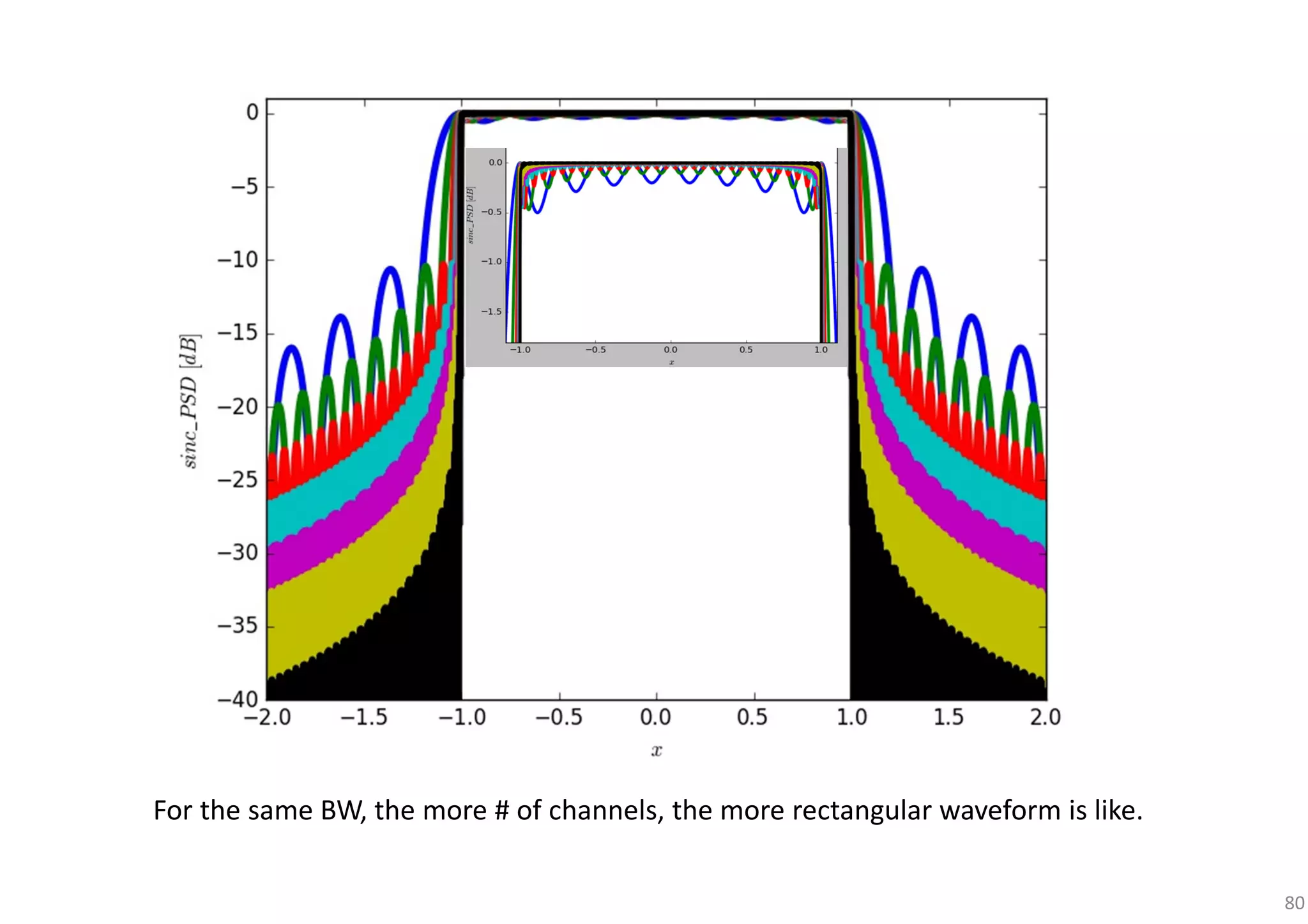
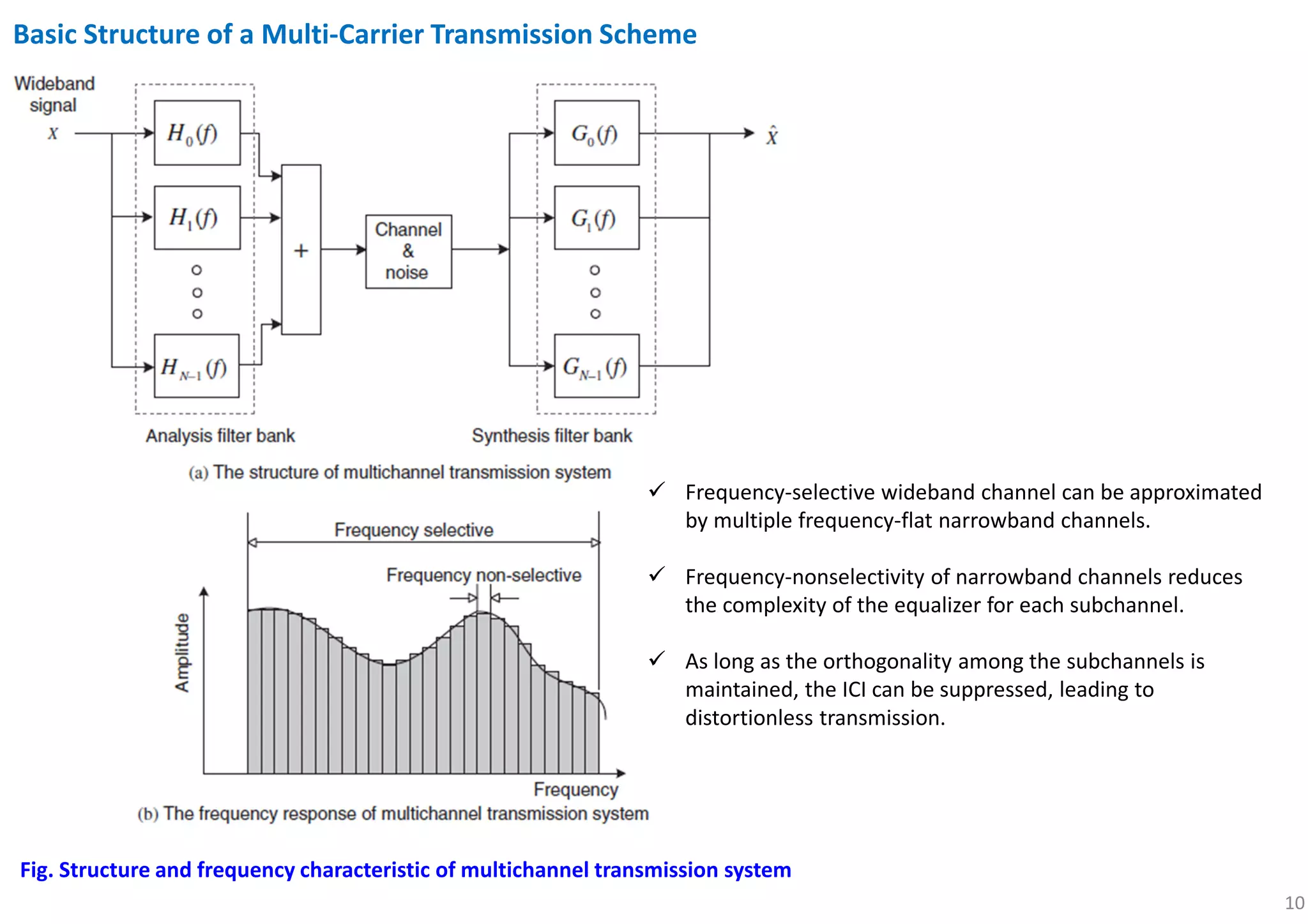
In a single-carrier transmission, higher data rate → need wider BW (assumed that channel is perfectly compensated by equalizer).
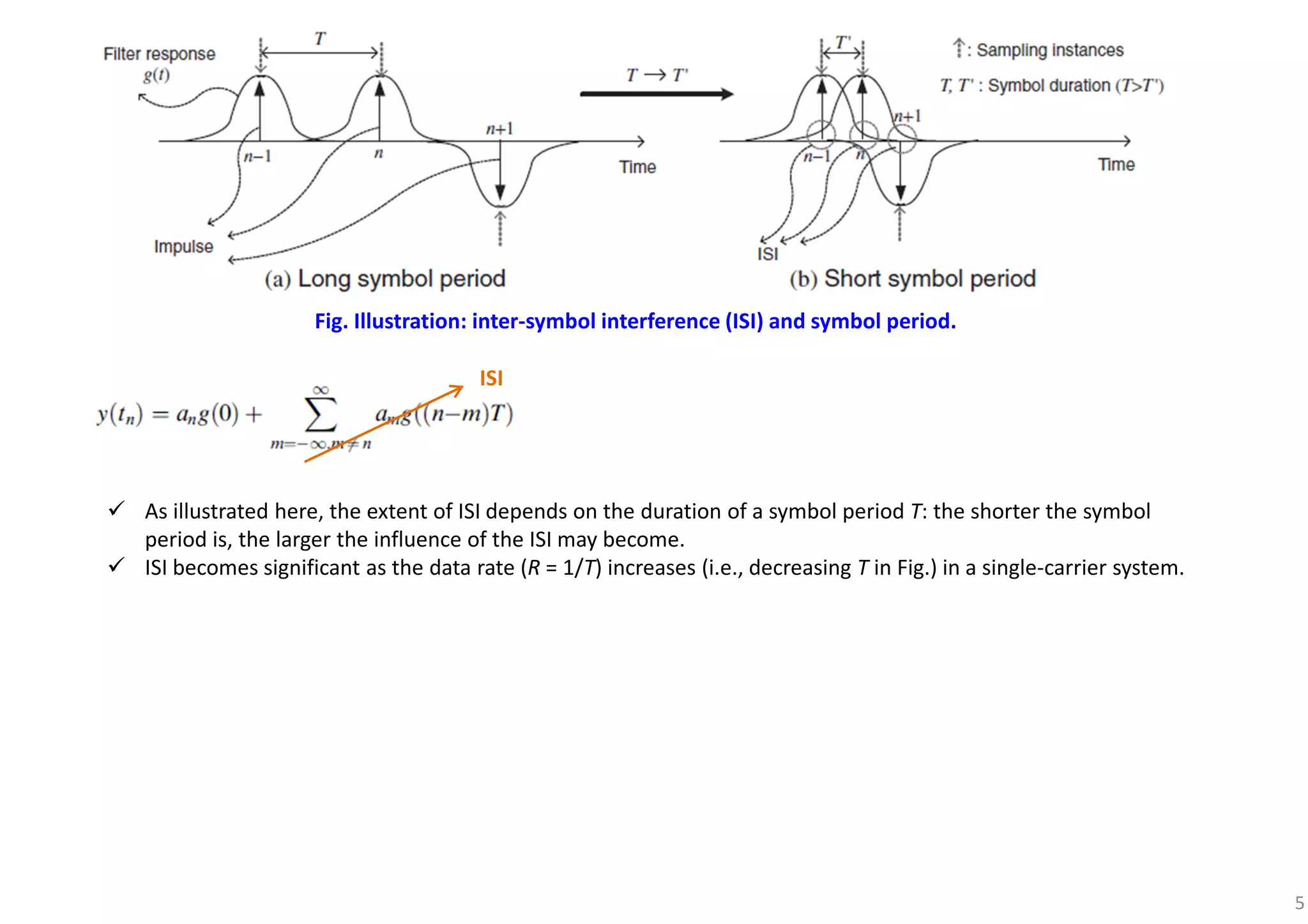
When the signal BW > coherence bandwidth in the wireless channel, the link suffers from multi-path fading, incurring ISI.
Adaptive equalizers are employed to deal with the ISI incurred by the time-varying multi-path fading channel.
The complexity of an equalizer increases with the data rate.
FIR filters with the adaptive tap coefficients that are adjusted so as to minimize the effect of ISI.
More equalizer taps are required as the ISI becomes significant.
The optimum detector for the multi-path fading channel is a maximum-likelihood sequence detector (MLSD), which bases on the
observation of a sequence of received symbols over successive symbol intervals, maximizing the posteriori probability.
(Complexity depends on the modulation order and the number of multi-paths).
Due to a memory of length L for the span of ISI, ML corresponding Euclidean distance path metrics must be evaluated to select the
best sequence in the MLSD.
6416 for L = 16 with 64-QAM at the data rate of 10 Mbps over the multi-path fading channel with a delay spread of 10 ms.
When M and L are too large, MMSE or LS equalizer, can be used.
The complexity of these suboptimum equalizers is still too enormous to be implemented as the ISI increases with the data rate.
A high data rate single-carrier transmission may not be feasible due to too much
complexity of the equalizer in the receiver.

10
Basic Structure of a Multi-Carrier Transmission Scheme
Frequency-selective wideband channel can be approximated
by multiple frequency-flat narrowband channels.
Frequency-nonselectivity of narrowband channels reduces
the complexity of the equalizer for each subchannel.
As long as the orthogonality among the subchannels is
maintained, the ICI can be suppressed, leading to
distortionless transmission.
Fig. Structure and frequency characteristic of multichannel transmission system

11
Fig. Structure and spectral characteristic of multicarrier transmission system.
FMT (Filtered Multi-Tone) transmission
FMT type of multicarrier transmission system can cope with the frequency selectivity of a wideband
channel.
But implementation becomes complex since it involves more encoders/decoders and oscillators,
and higher quality filters as # subcarriers increases.

12
OFDM Transmission Scheme
OFDM scheme places a guard band at outer
subcarriers, called virtual carriers (VCs),
around the frequency band to reduce the
out of band radiation.
OFDM scheme also inserts a guard interval in
the time domain, called cyclic prefix (CP),
which mitigates the ISI between OFDM
symbols.

14
Comparison between the single-carrier and multi-carrier transmission schemes

15
Coded OFDM
Duplexing
Agenda

16
Basic Principle of OFDM: Orthogonality

19
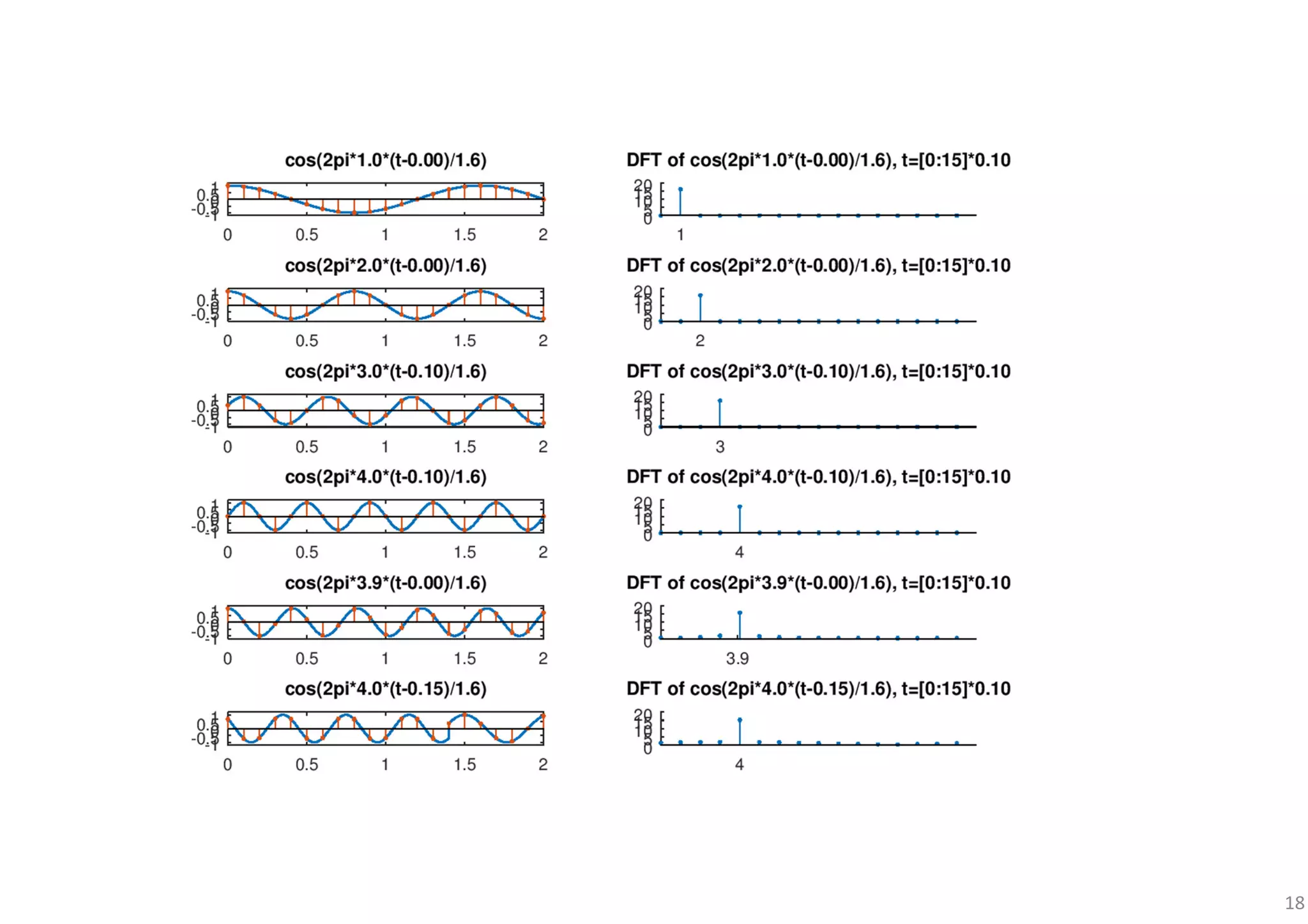
% to plot several sinusoidal signals with different frequencies/phases and their DFT sequences to check their orthogonality
% {exp(j2π*fk*t)},0≤k≤N-1，fk=k/Tsym
clear,close,clc all
T = 1.6; % period = 1.6s in equations is Tsym
ND = 1000;
nn = 0:ND;
ts = 0.002;
tt = nn*ts; % time interval 0, 0.002, 0.004..., 2 [x-axis]
Ts =0.1; % Sampling period in continuous time
M = round(Ts/ts); % Sampling period in discrete time
nns = [1:M:ND+1]; % Sampling indices
tts = (nns-1)*ts; % Sampling times
ks = [1:4 3.9 4]; % Frequency indices
tds = [0 0 0.1 0.1 0 0.15]; %delay times
K = length(ks);
for i = 1:K
k = ks(i);
td = tds(i);
x(i,:) = exp(j*2*pi*k*(tt-td)/T); % [y-axis]
if i == K
x(K,:) = [x(K,[302:end]) x(K-3,[1:301])];
endif
title_string = sprintf('cos(2pi*%1.1f*(t-%4.2f)/%2.1f)',k,td,T);
subplot(K,2,2*i-1); % 6 x 2
plot(tt,real(x(i,:)),'LineWidth',1); title(title_string);
hold on;
plot(tt([1 end]),[0 0],'k'); % plot([xi xf],[yi yf])
set(gca,'fontsize',10);
axis([tt([1 end]) -1.2 1.2]); % axis([xi xf yi yf])
stem(tts,real(x(i,nns)),'.','markersize',7);
endfor
N = round(T/Ts);
xn = x(:,nns(1:N));
xn*xn'/N % check orthogonality
Xk = fft(xn.').';
kk = 0:N-1;
for i = 1:K
k = ks(i);
td = tds(i);
title_string = sprintf('DFT of cos(2pi*%1.1f*(t-%4.2f)/%2.1f), t=[0:%d]*%3.2f',k,td,T,N-1,Ts);
subplot(K,2,2*i); % 6 x 2
stem(kk,abs(Xk(i,:)),'.','markersize',7); title(title_string);
set(gca,'fontsize',10,'xtick',[k]);
axis([0 N 0 20]);
endfor
https://gist.github.com/oklachumi/f41c1f5af7e9f3c1684307d5575753b1

20
OFDM Modulation and Demodulation: Tx
1. OFDM transmitter maps the message bits into a sequence of PSK or QAM symbols.
2. A sequence of PSK or QAM symbols will be subsequently converted into N parallel streams.
3. Each of N symbols from serial-to-parallel (S/P) conversion is carried out by the different subcarrier.

21
OFDM Modulation and Demodulation: Rx

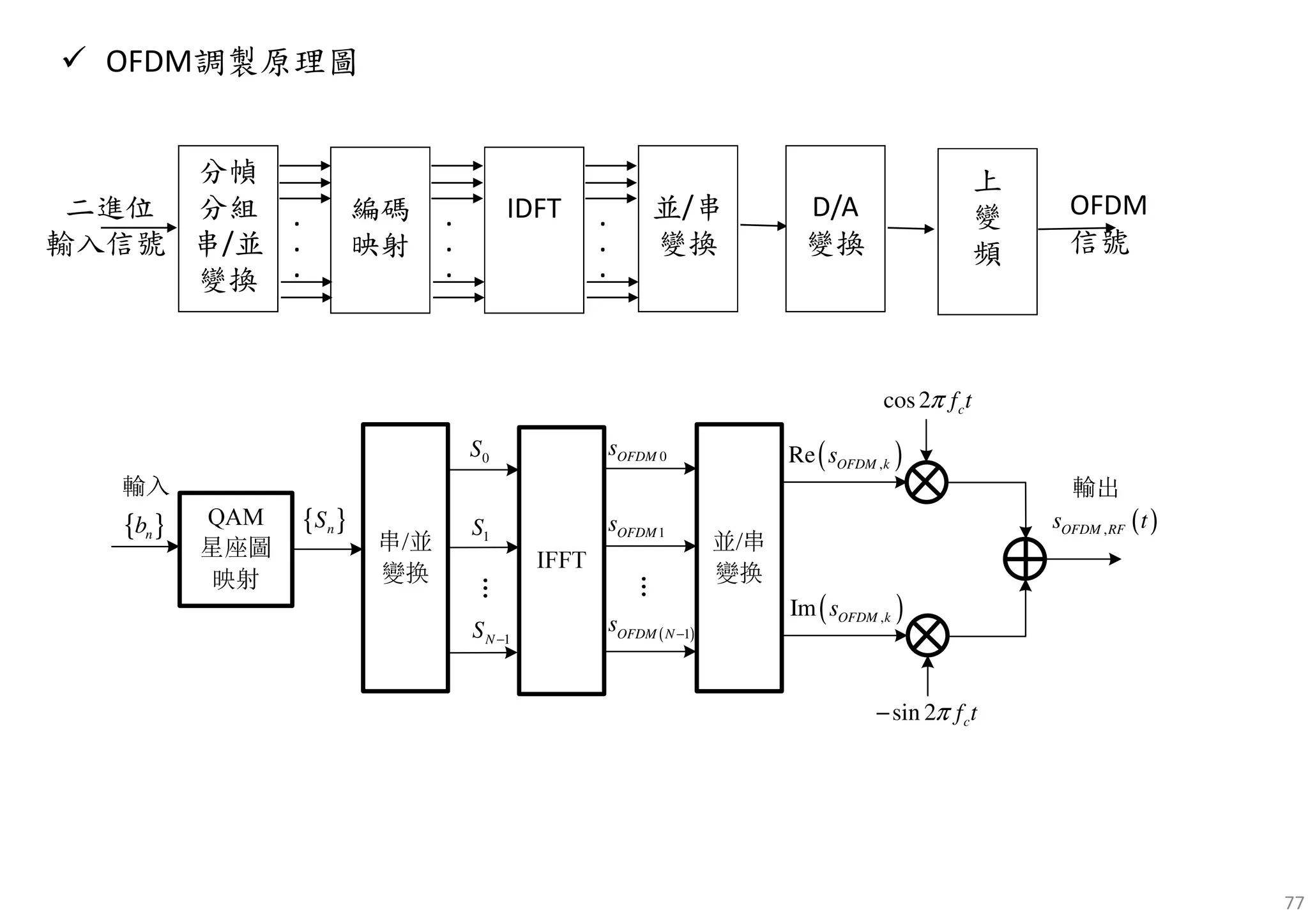
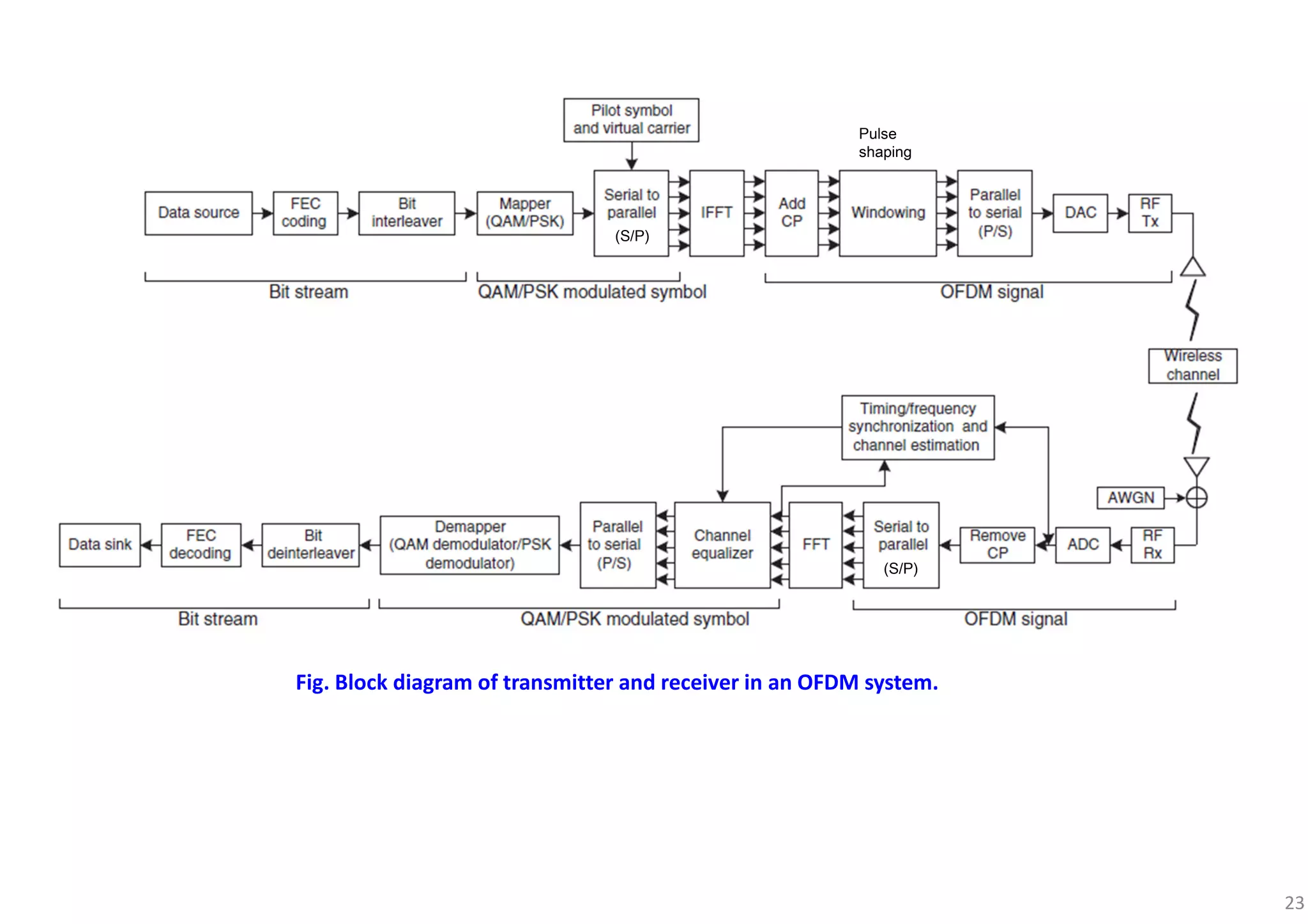
22Fig. Illustrative block diagram of OFDM modulation and demodulation: N = 6.
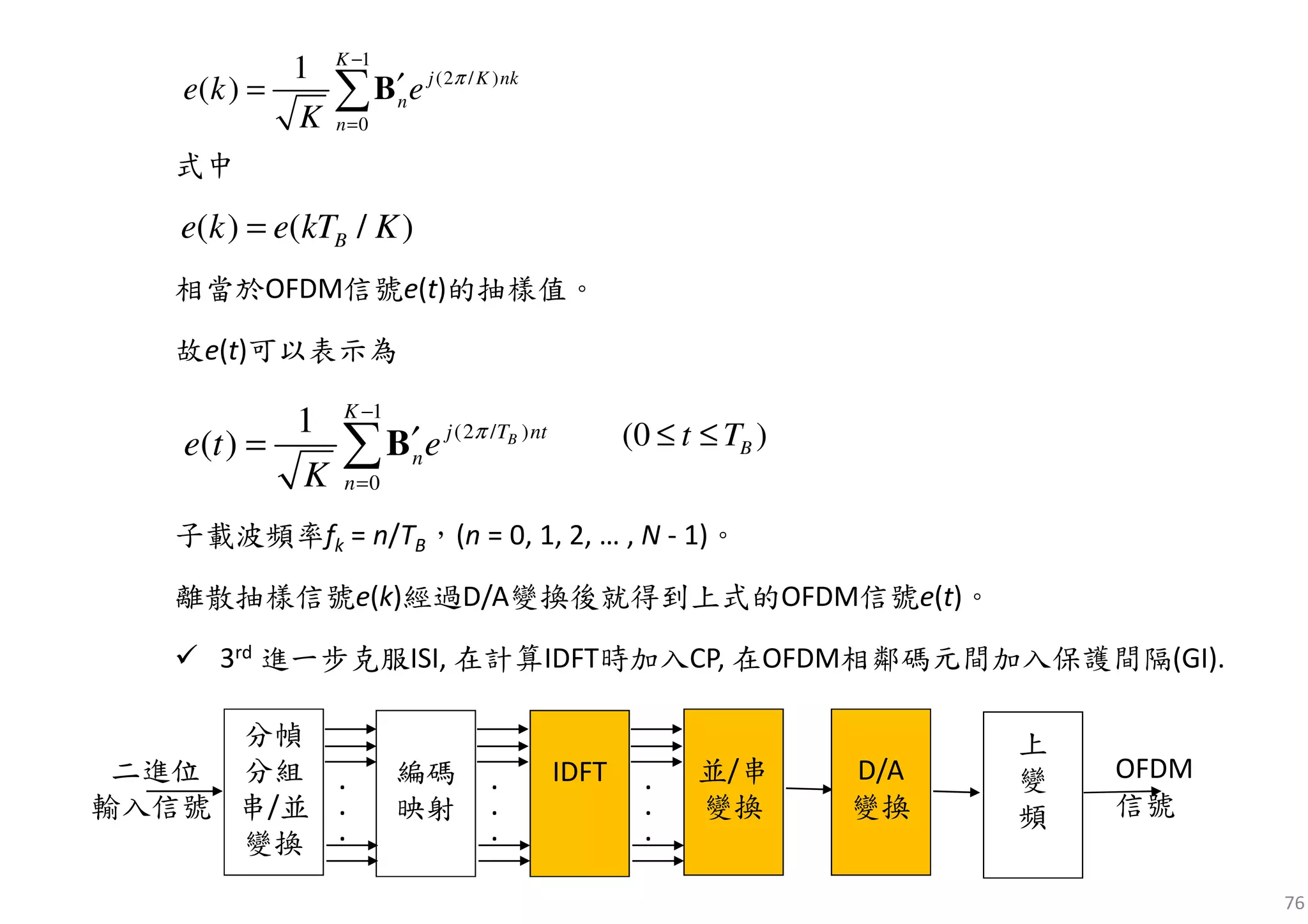
continuous-time baseband OFDM signal
discrete-time OFDM symbol
The frequency-domain symbol X[k] modulates the subcarrier with a frequency of fk = k/Tsym.
Original symbol X[k] has simpling period Ts, but its length has been extended to Tsym = NTs by
transmitting N symbols in a parallel form.

23
Fig. Block diagram of transmitter and receiver in an OFDM system.
(S/P)
Pulse
shaping
(S/P)

24
Effect of Multipath Channel on OFDM Symbols

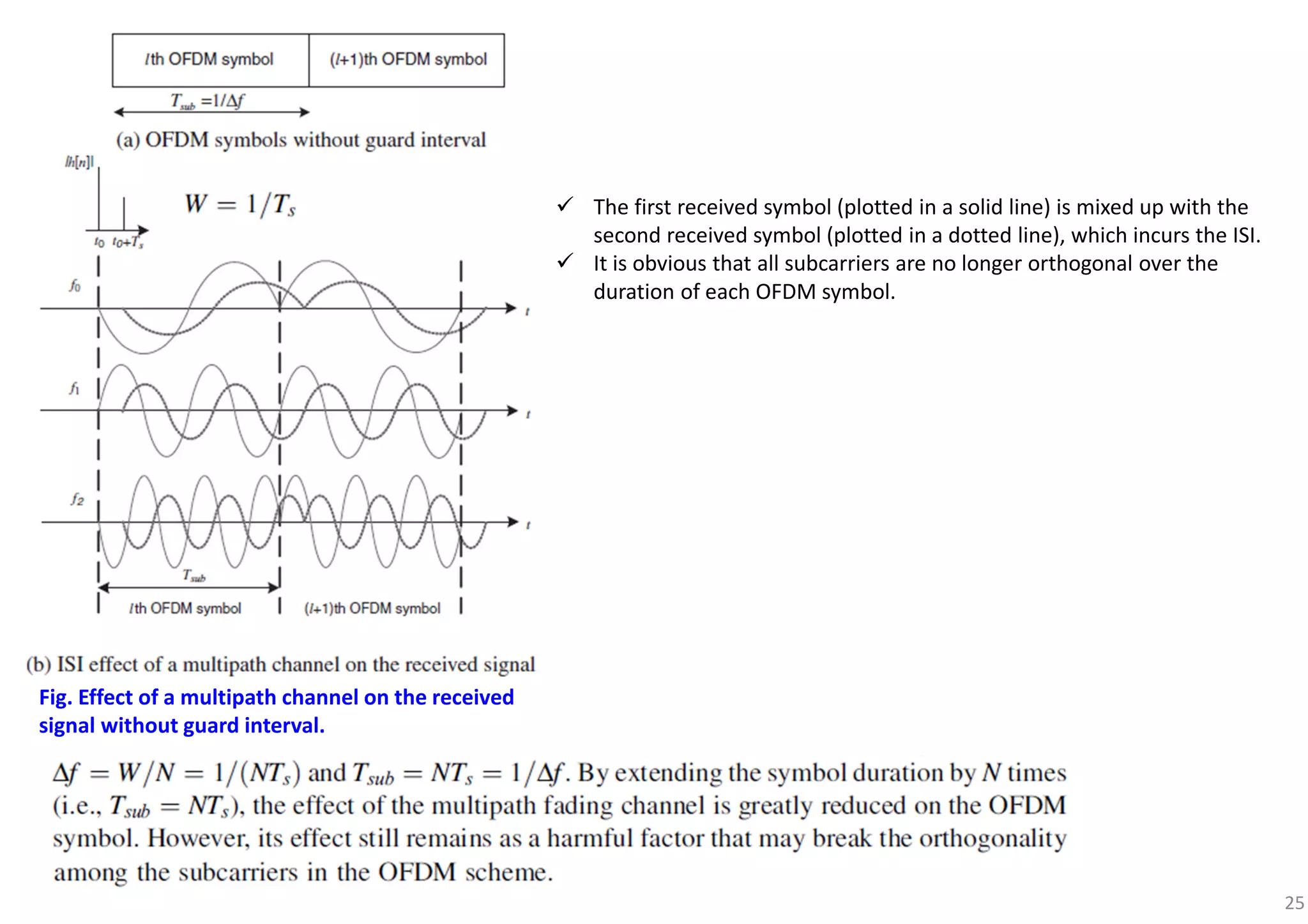
25
The first received symbol (plotted in a solid line) is mixed up with the
second received symbol (plotted in a dotted line), which incurs the ISI.
It is obvious that all subcarriers are no longer orthogonal over the
duration of each OFDM symbol.
Fig. Effect of a multipath channel on the received
signal without guard interval.

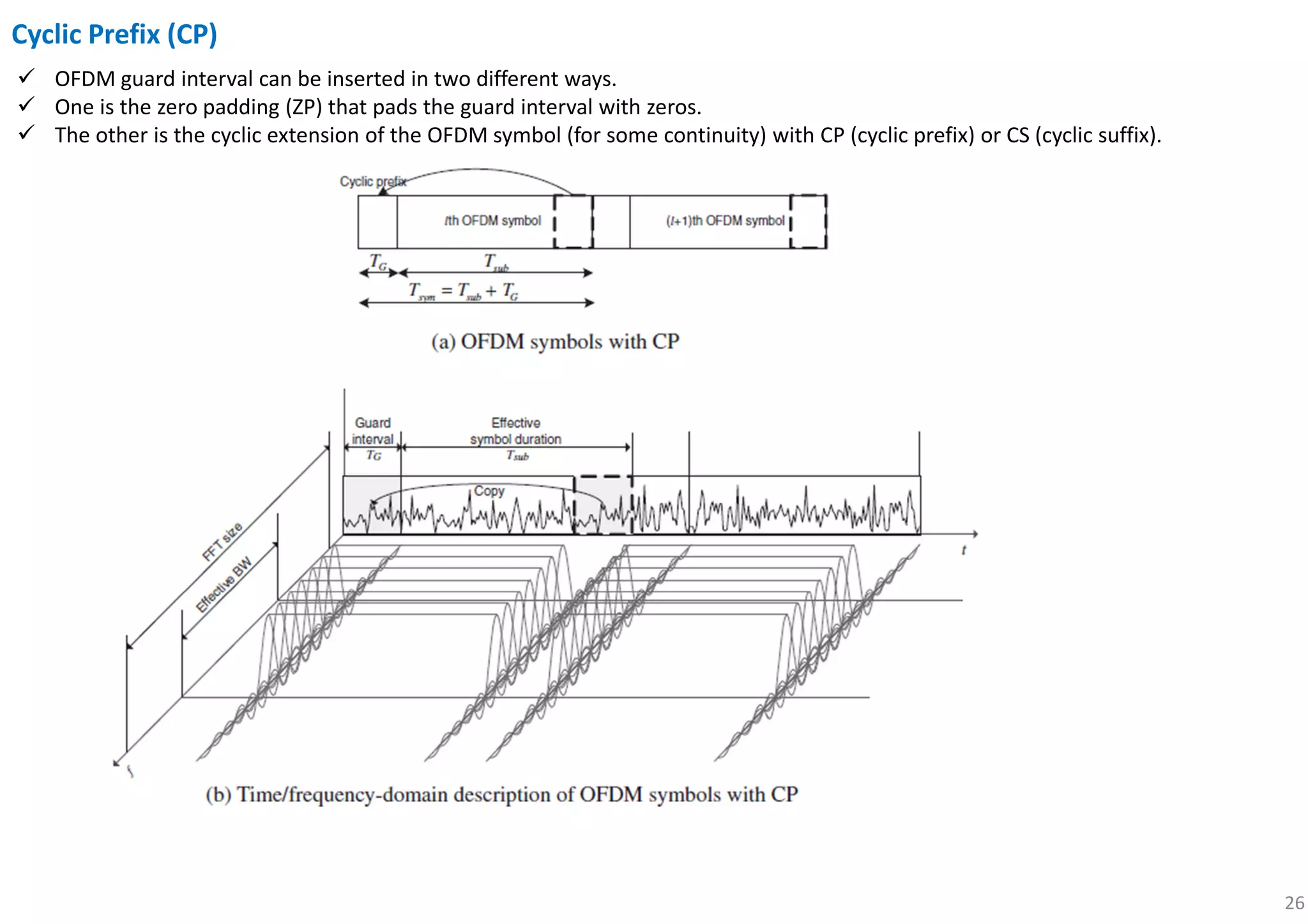
26
Cyclic Prefix (CP)
OFDM guard interval can be inserted in two different ways.
One is the zero padding (ZP) that pads the guard interval with zeros.
The other is the cyclic extension of the OFDM symbol (for some continuity) with CP (cyclic prefix) or CS (cyclic suffix).

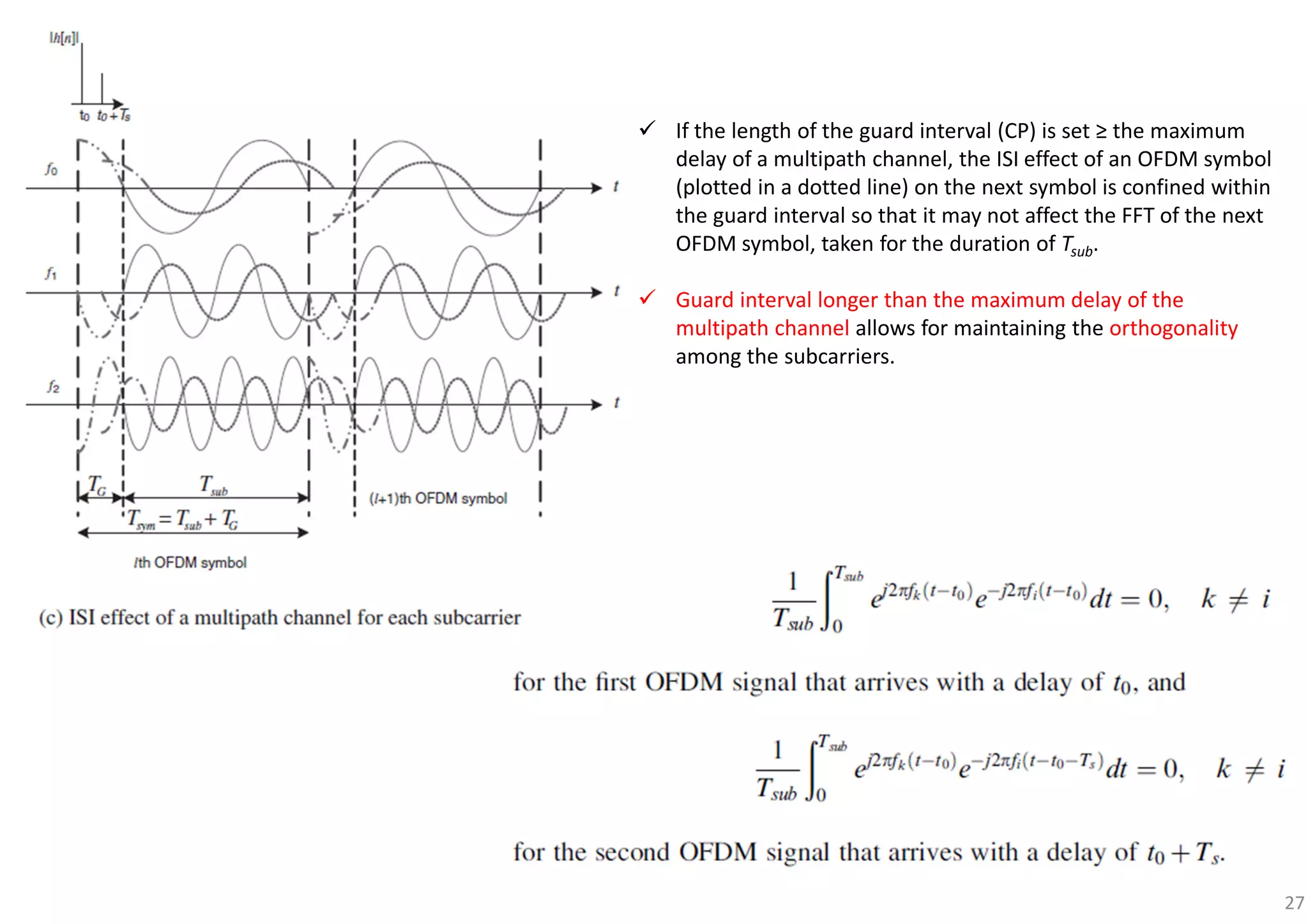
27
If the length of the guard interval (CP) is set ≥ the maximum
delay of a multipath channel, the ISI effect of an OFDM symbol
(plotted in a dotted line) on the next symbol is confined within
the guard interval so that it may not affect the FFT of the next
OFDM symbol, taken for the duration of Tsub.
Guard interval longer than the maximum delay of the
multipath channel allows for maintaining the orthogonality
among the subcarriers.

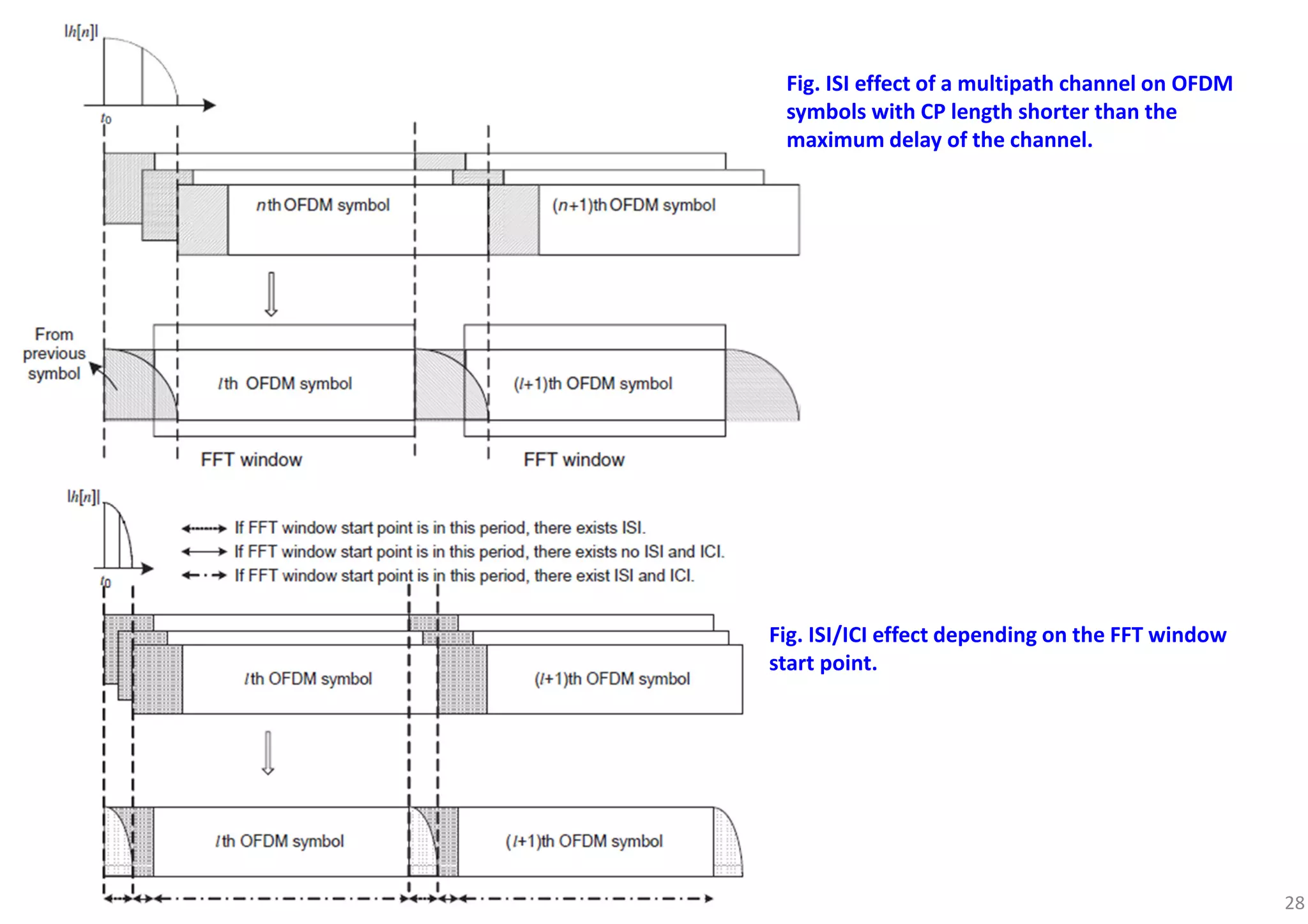
28
Fig. ISI/ICI effect depending on the FFT window
start point.
Fig. ISI effect of a multipath channel on OFDM
symbols with CP length shorter than the
maximum delay of the channel.

29
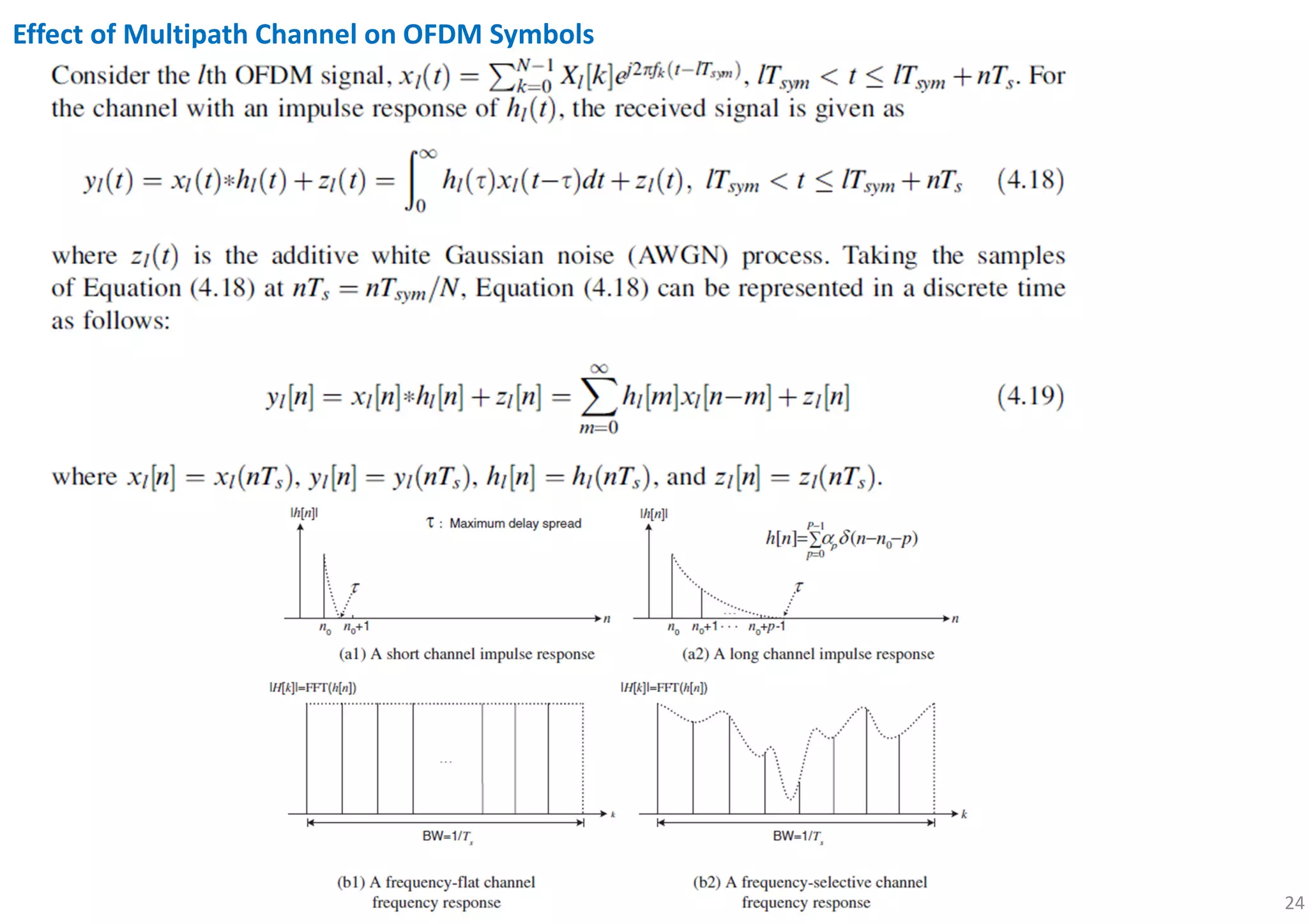
Suppose:
1. CP length is set ≥ the maximum delay of the channel.
2. The FFT window start point of an OFDM symbol is determined within its CP interval (i.e., unaffected by the previous symbol).
The OFDM receiver takes the FFT of the received samples:
Fig. Frequency-domain equivalent model of OFDM system.
circular convolution!!
Insertion CP in the transmitter makes the transmit samples
circularly-convolved with the channel samples, which yields
as desired in the receiver.[ ] [ ] [ ]l l lY k H k X k=

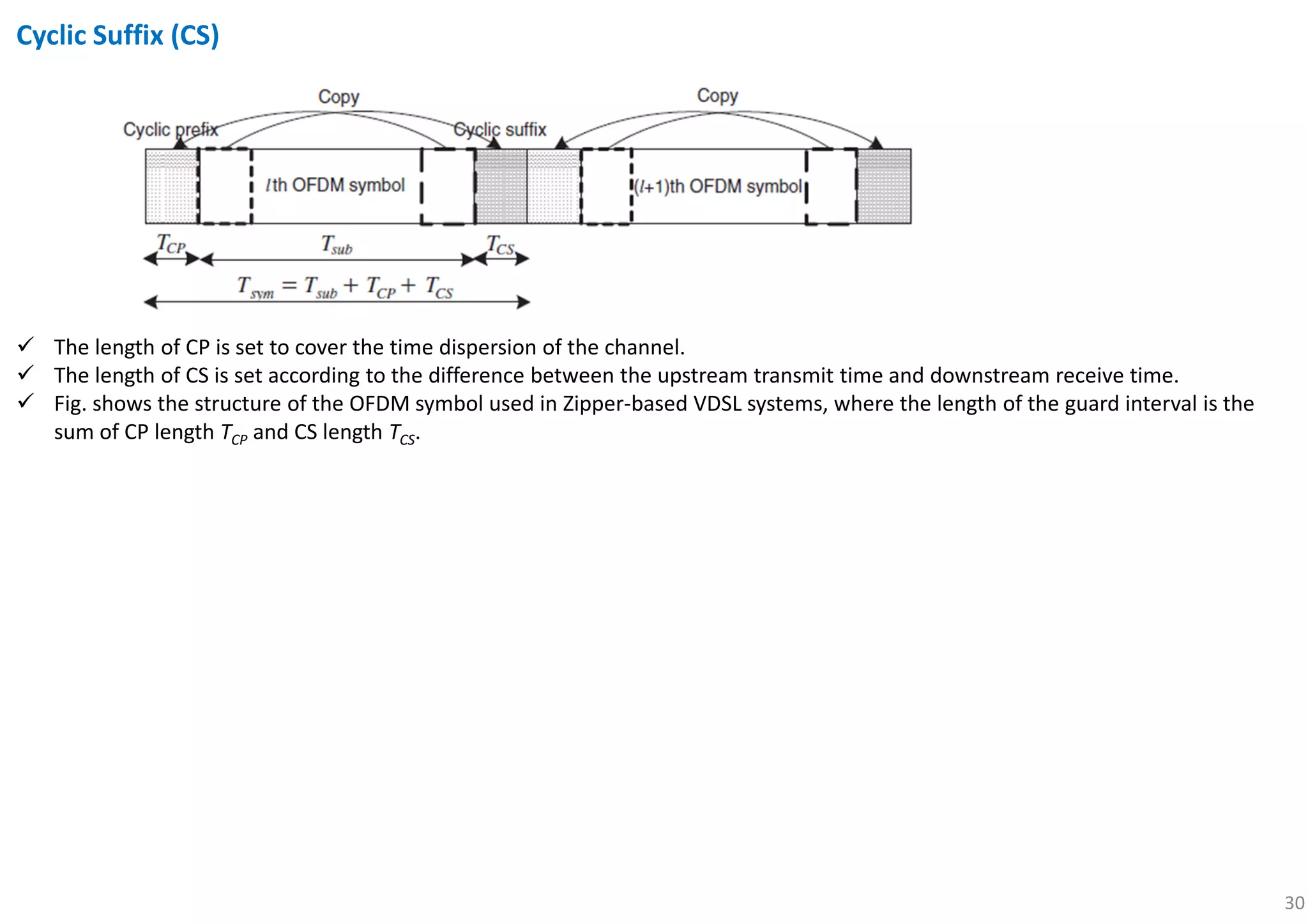
30
Cyclic Suffix (CS)
The length of CP is set to cover the time dispersion of the channel.
The length of CS is set according to the difference between the upstream transmit time and downstream receive time.
Fig. shows the structure of the OFDM symbol used in Zipper-based VDSL systems, where the length of the guard interval is the
sum of CP length TCP and CS length TCS.

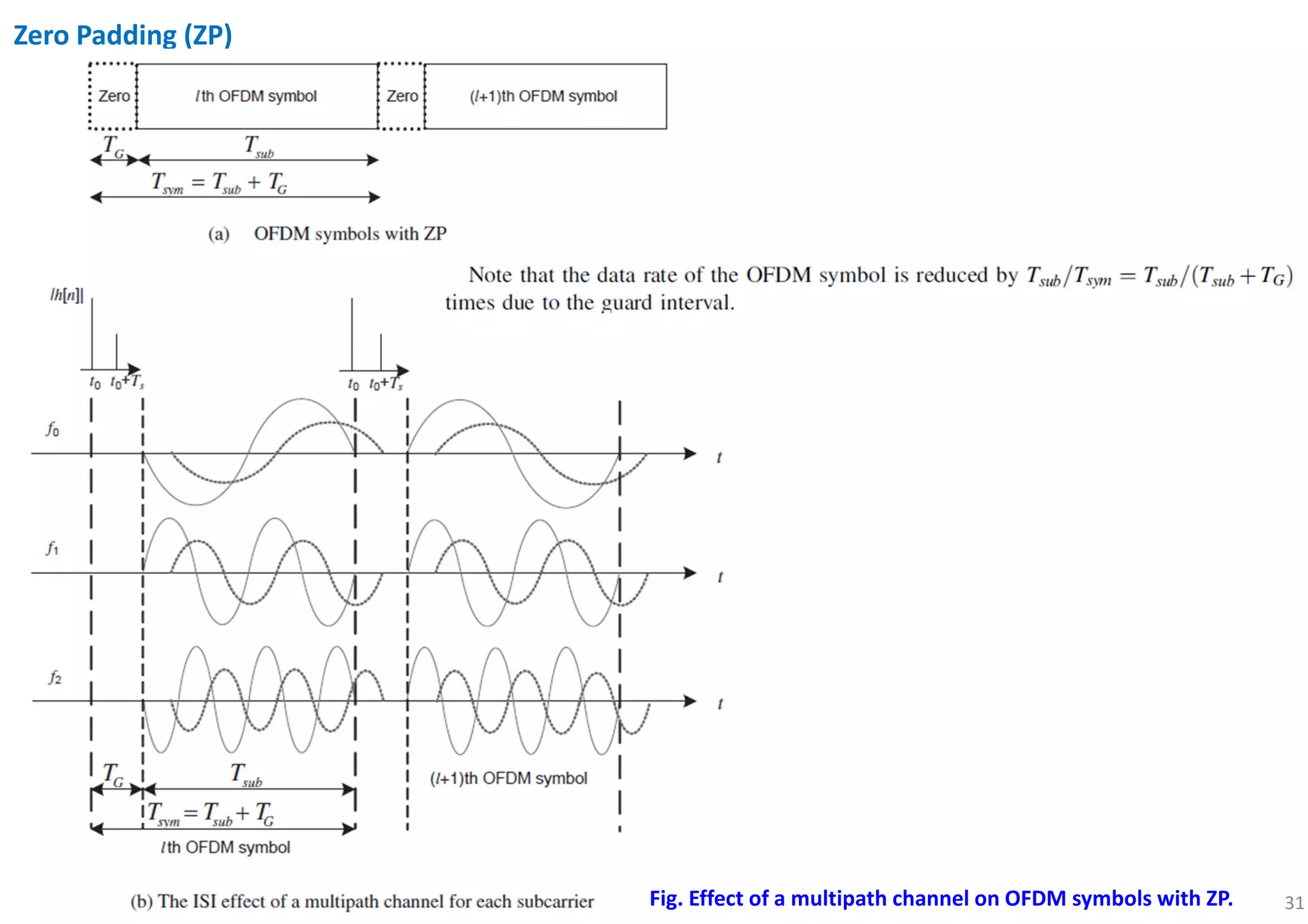
31
Zero Padding (ZP)
Fig. Effect of a multipath channel on OFDM symbols with ZP.

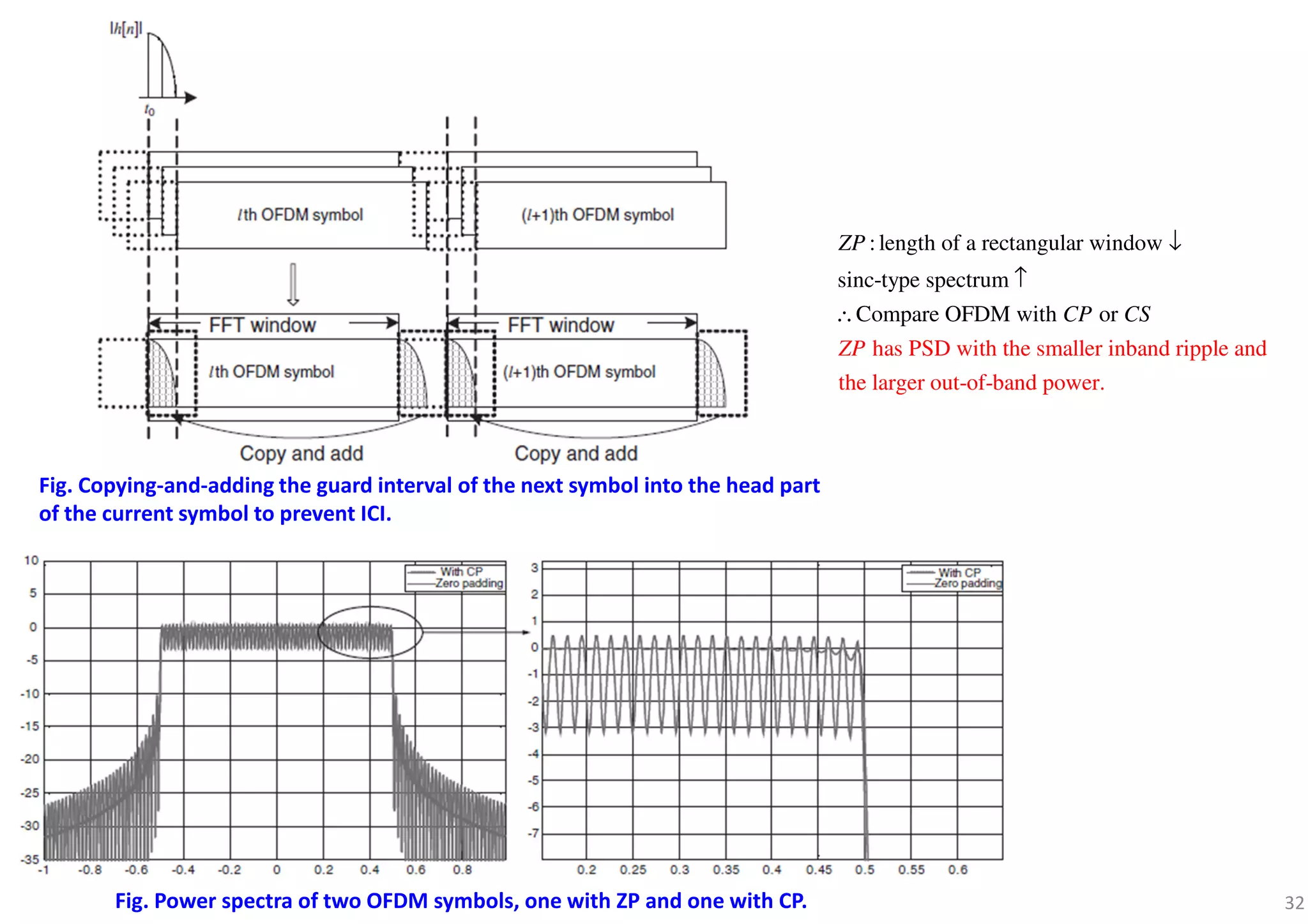
32
Fig. Copying-and-adding the guard interval of the next symbol into the head part
of the current symbol to prevent ICI.
Fig. Power spectra of two OFDM symbols, one with ZP and one with CP.
:length of a rectangular window
sinc-type spectrum
Compare OFDM with or
has PSD with the smaller inband ripple and
the larger out-of-band power.
ZP
S
ZP
CP C
↓
↑
∴

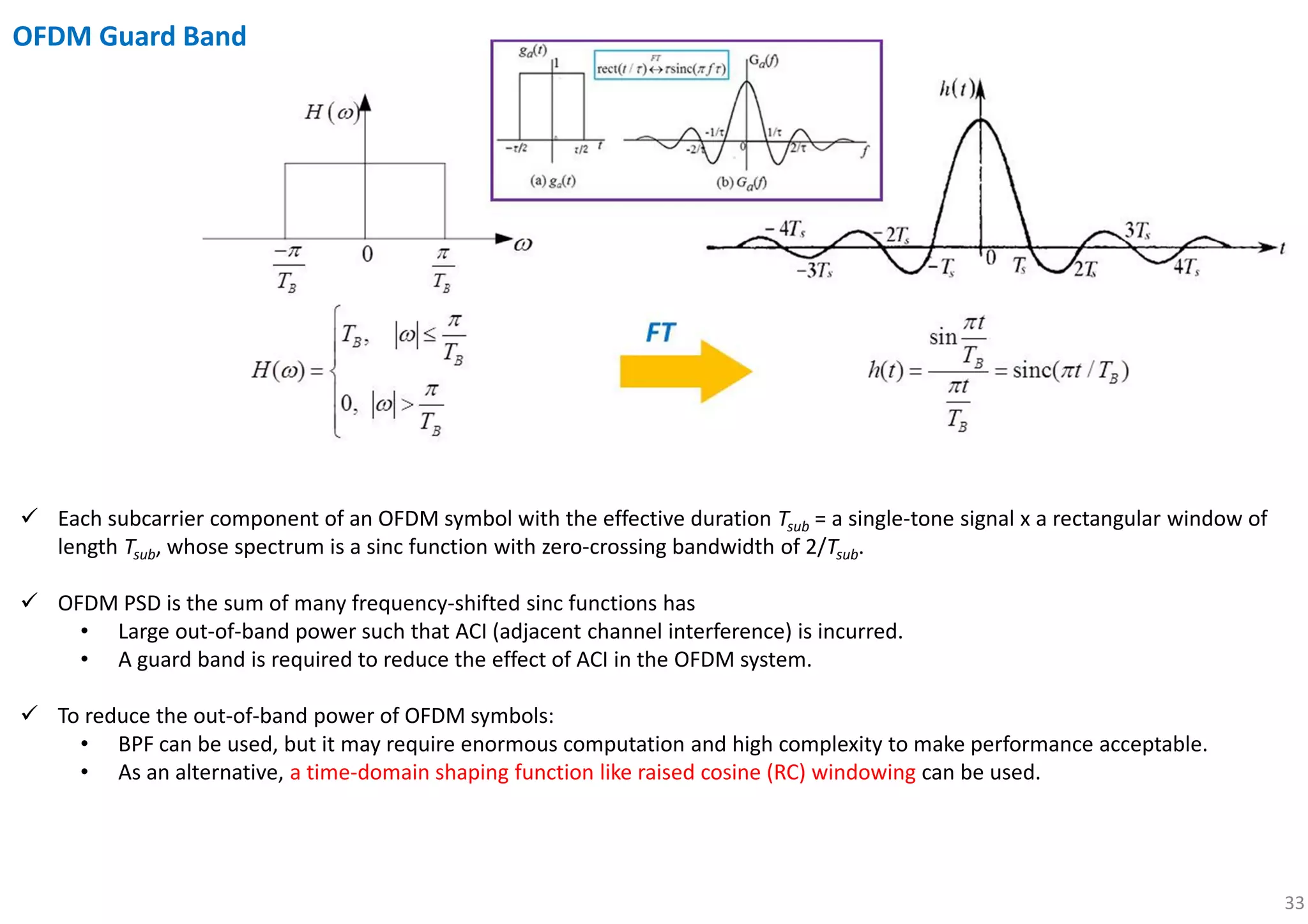
33
OFDM Guard Band
Each subcarrier component of an OFDM symbol with the effective duration Tsub = a single-tone signal x a rectangular window of
length Tsub, whose spectrum is a sinc function with zero-crossing bandwidth of 2/Tsub.
OFDM PSD is the sum of many frequency-shifted sinc functions has
• Large out-of-band power such that ACI (adjacent channel interference) is incurred.
• A guard band is required to reduce the effect of ACI in the OFDM system.
To reduce the out-of-band power of OFDM symbols:
• BPF can be used, but it may require enormous computation and high complexity to make performance acceptable.
• As an alternative, a time-domain shaping function like raised cosine (RC) windowing can be used.

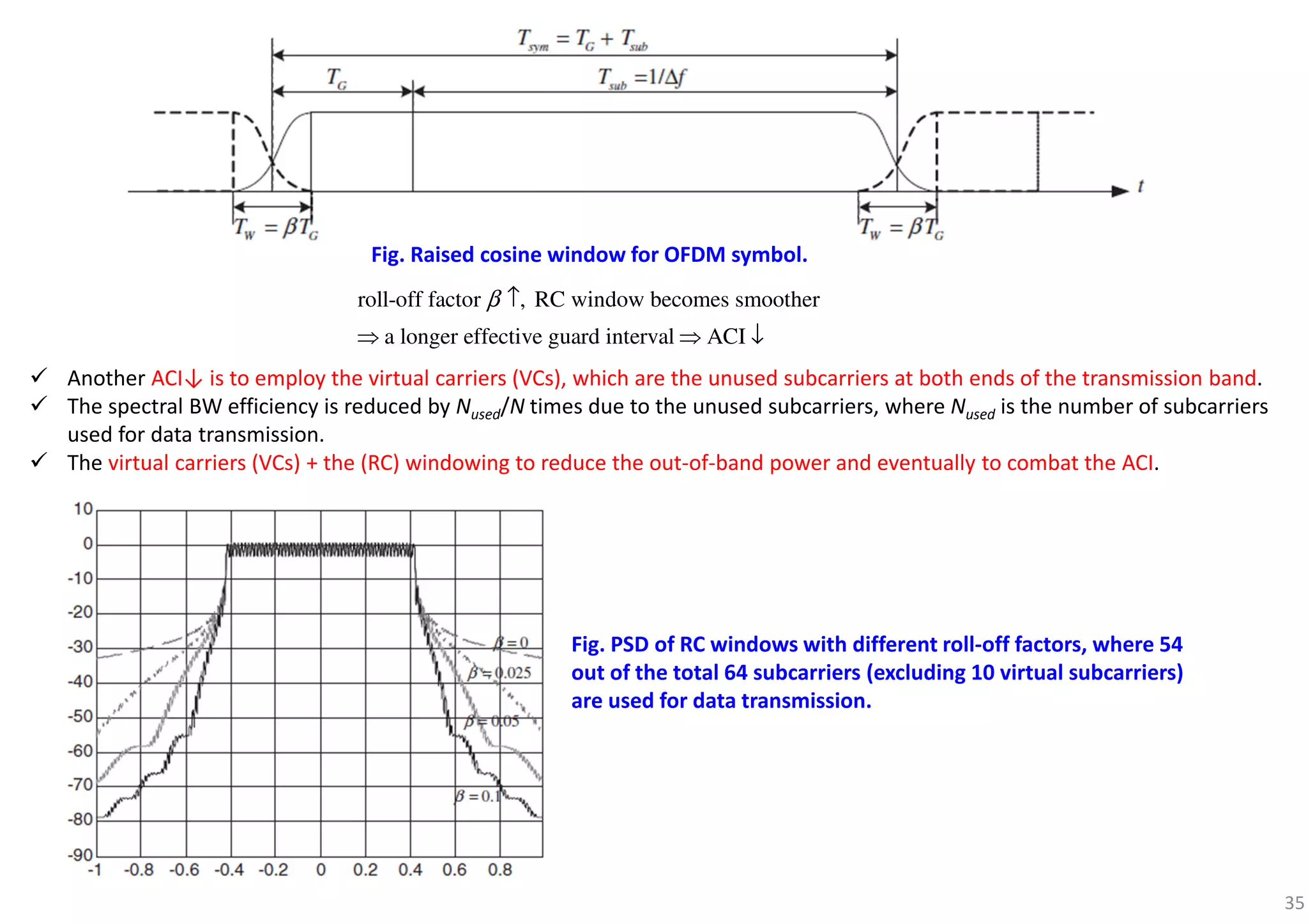
35
Fig. Raised cosine window for OFDM symbol.
roll-off factor , RC window becomes smoother
a longer effective guard interval ACI
β ↑
⇒ ⇒ ↓
Another ACI↓ is to employ the virtual carriers (VCs), which are the unused subcarriers at both ends of the transmission band.
The spectral BW efficiency is reduced by Nused/N times due to the unused subcarriers, where Nused is the number of subcarriers
used for data transmission.
The virtual carriers (VCs) + the (RC) windowing to reduce the out-of-band power and eventually to combat the ACI.
Fig. PSD of RC windows with different roll-off factors, where 54
out of the total 64 subcarriers (excluding 10 virtual subcarriers)
are used for data transmission.

38
Review…Coverting Bit Stream into Symbol Stream

39
Review…Modulation - Mapping Symbols onto a Constellation

41
Review…Demodulation - Demapping a Constellation to a Symbol

42
Review…Converting a Symbol to Bits

44
clear,close,clc all
N = 1000; % # of data
mlevel = 4; % QAM = 4, 16 QAM = 16 and so on
k = log2(mlevel); % # of bits per symbol
% signal generation in bit stream
x = randi([0 1],N,1); % 1000*1
% convert the bit stream into symbol stream
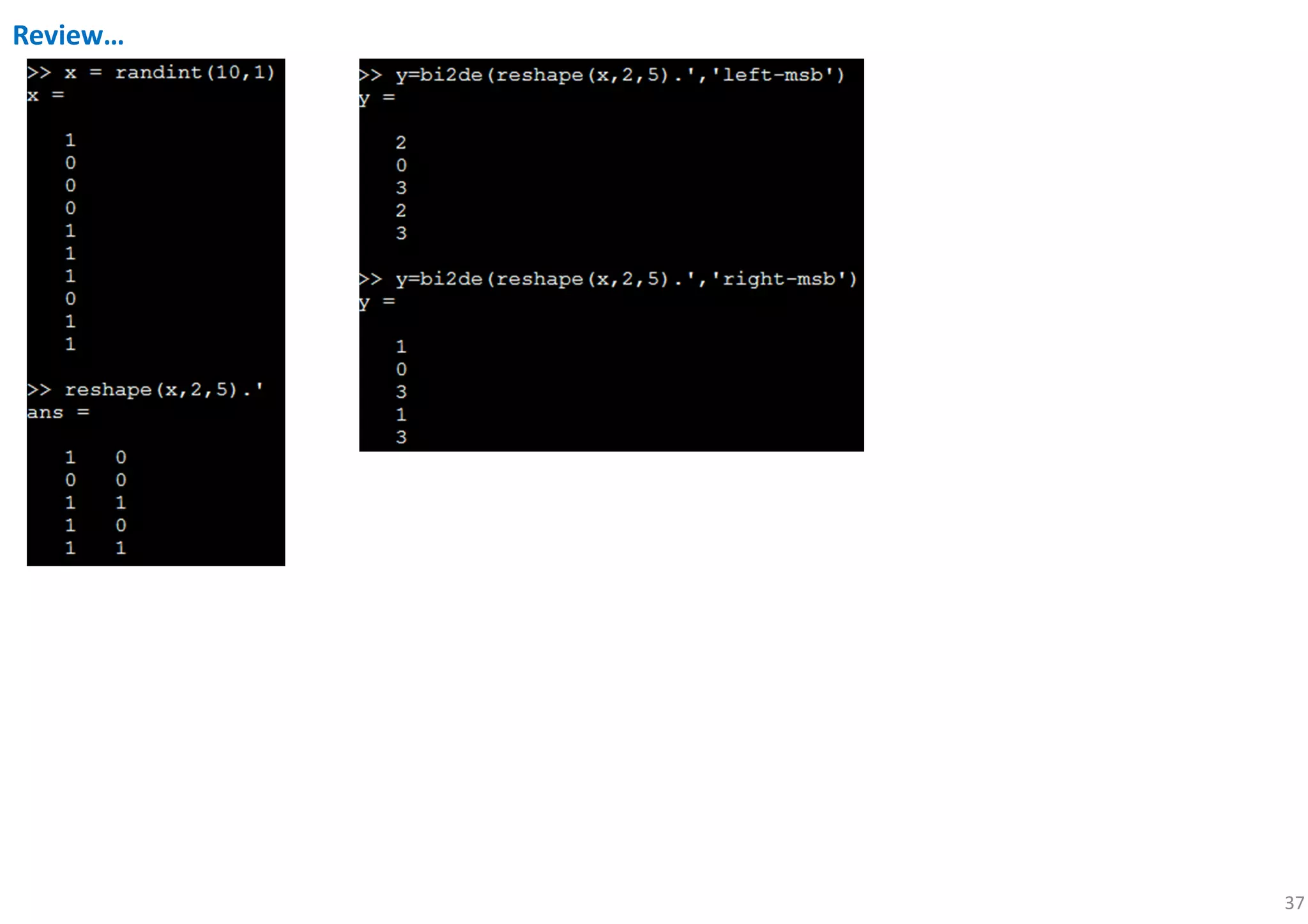
xsym = bi2de(reshape(x,k,length(x)/k).'); %500*1
% modulation
xmod = qammod(xsym,mlevel);
Tx_x = xmod;
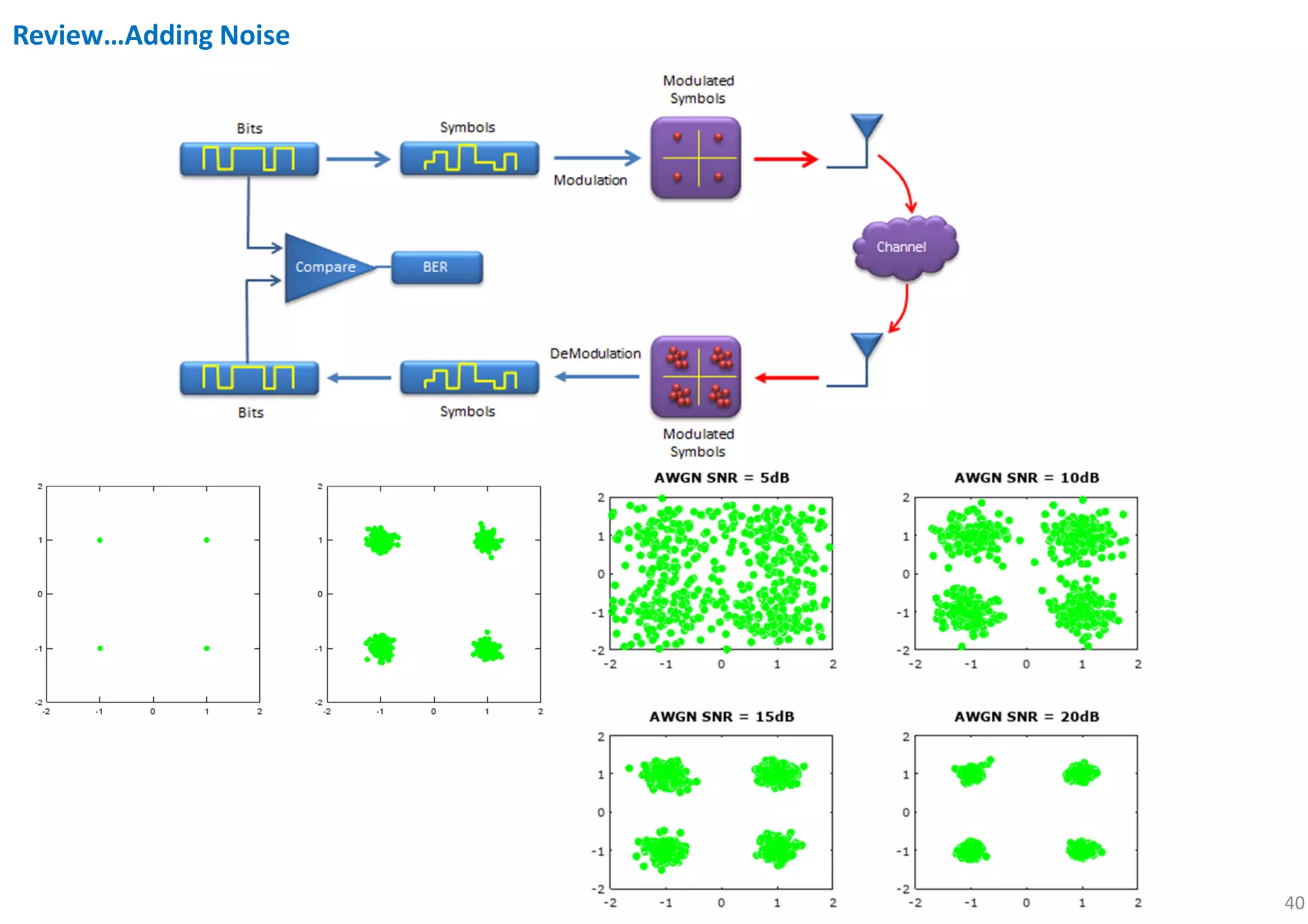
% adding AWGN
SNR = 1;
Tx_awgn = awgn(Tx_x,SNR,'measured');
% Received signal
Rx_x = Tx_awgn;
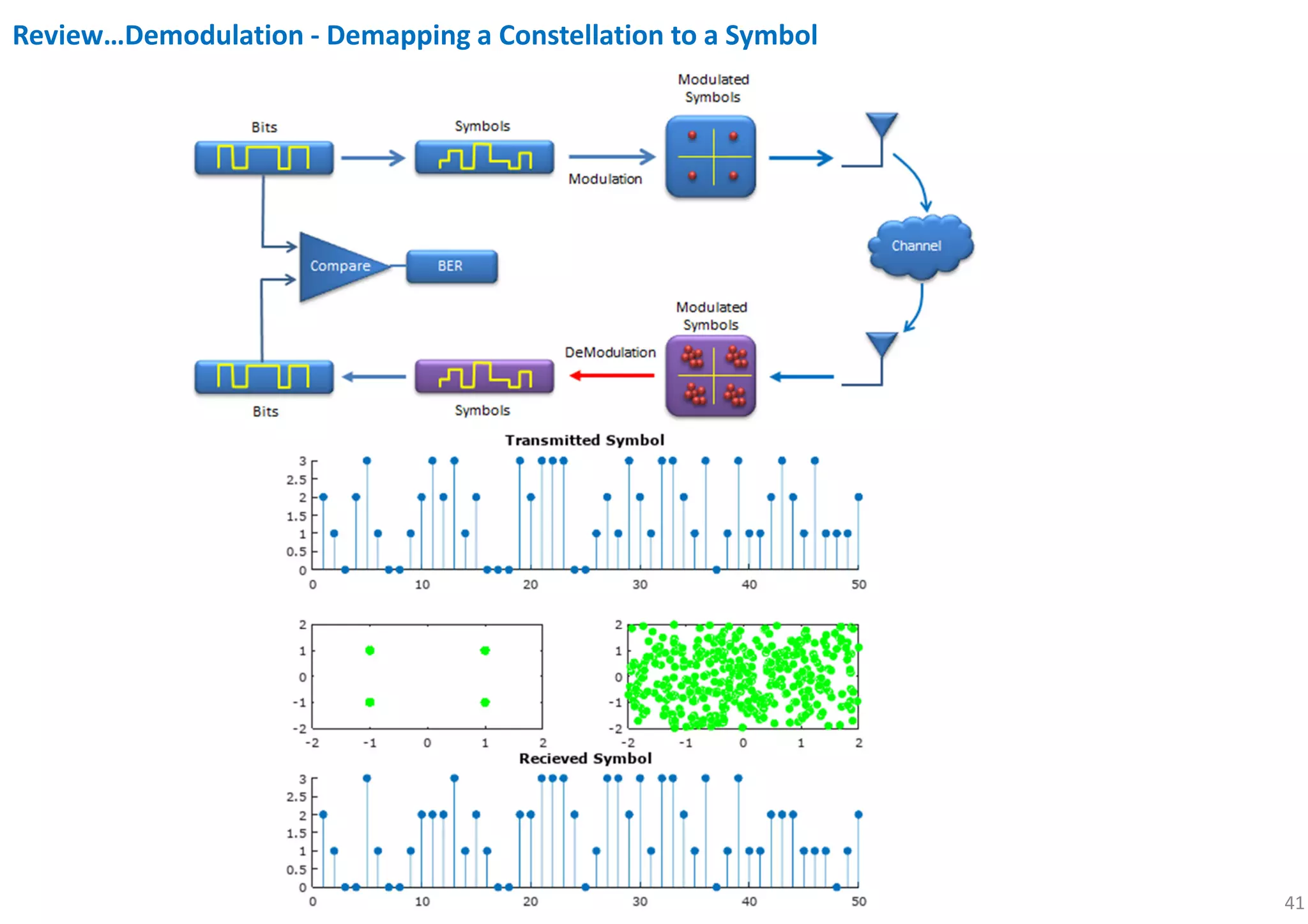
%demodulation
Rx_x_demod = qamdemod(Rx_x,mlevel);
z = de2bi(Rx_x_demod); % Convert integers to bits.
% Convert z from a matrix to a vector.
Rx_x_BitStream = reshape(z.',prod(size(z)),1);
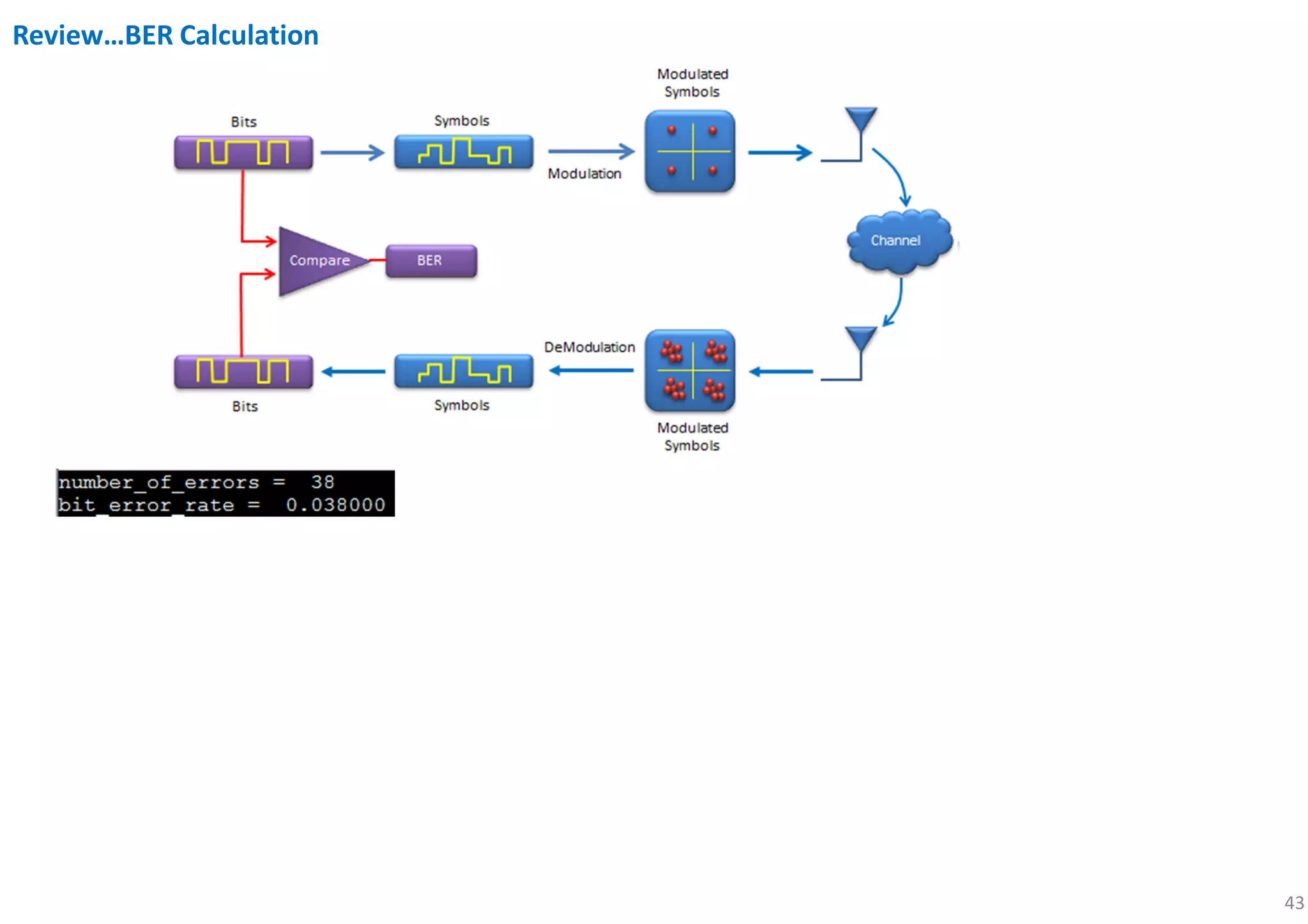
[number_of_errors, bit_error_rate] = biterr(x, Rx_x_BitStream)
%plot each steps
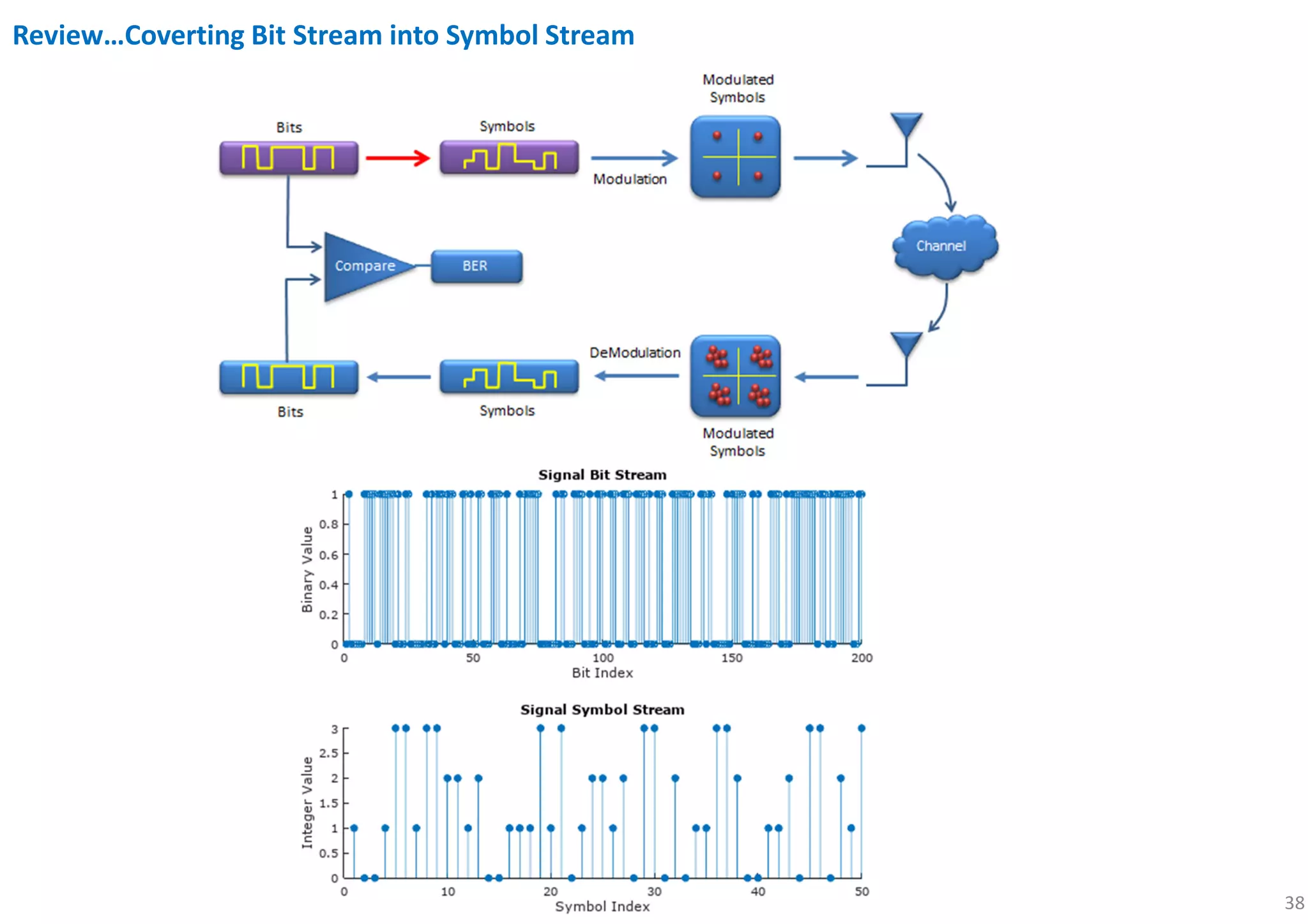
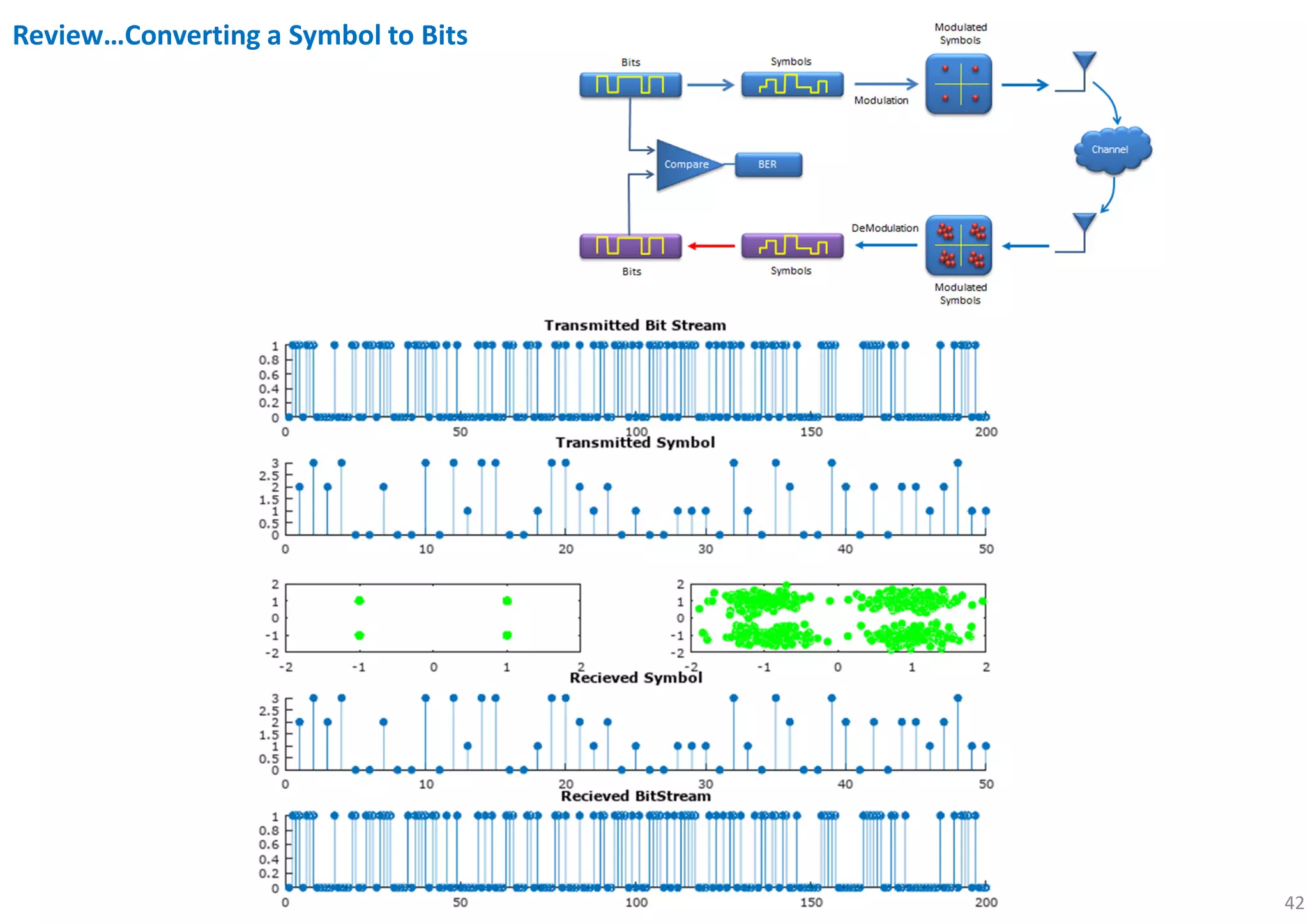
subplot(5,2,[1 2]); stem(x(1:200),'filled'); title('Transmitted Bit Stream');
subplot(5,2,[3 4]); stem(xsym(1:50),'filled'); title('Transmitted Symbol');
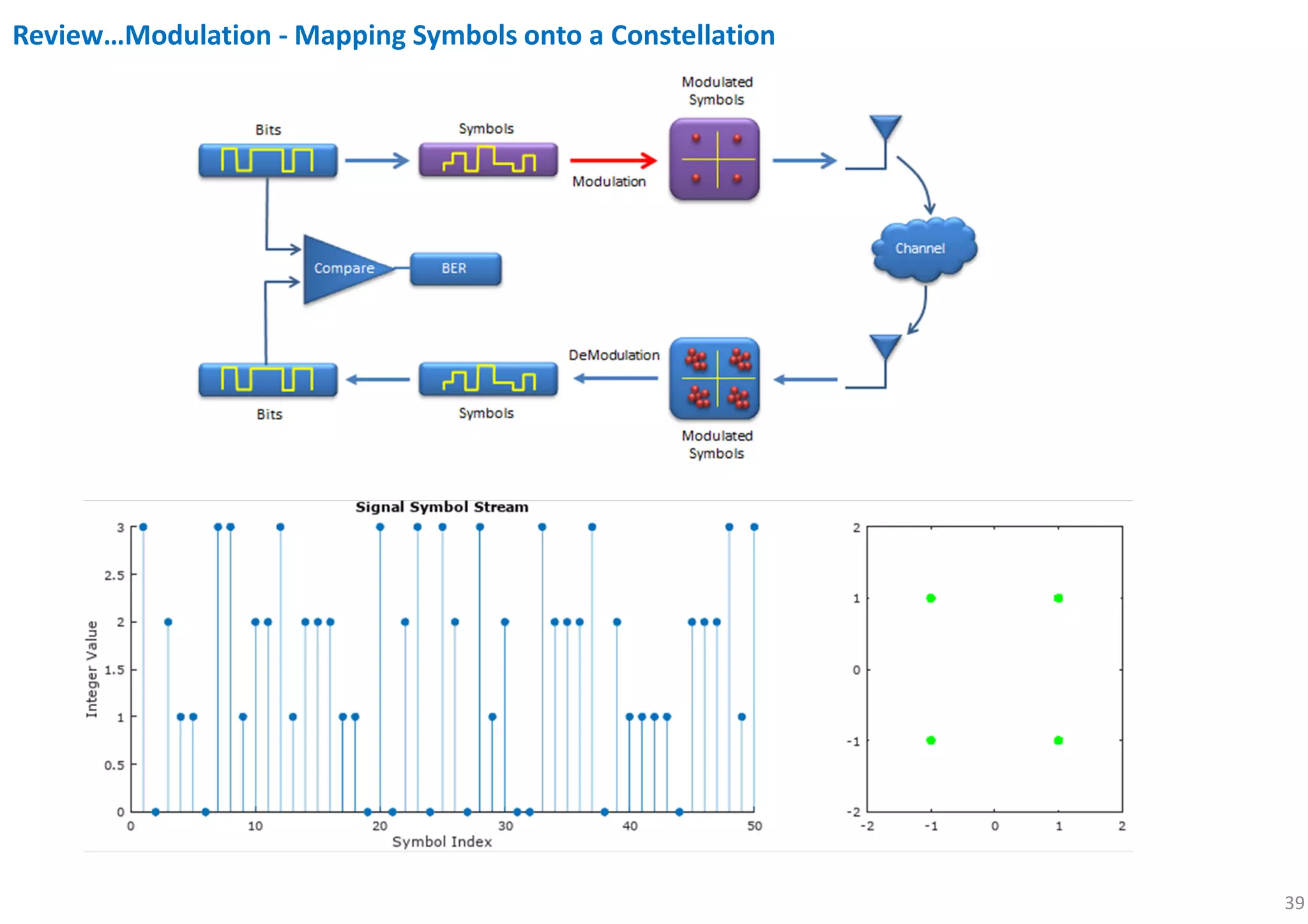
subplot(5,2,5); plot(real(Tx_x),imag(Tx_x),'go','MarkerFaceColor',[0,1,0]);
axis([-mlevel/2 mlevel/2 -mlevel/2 mlevel/2]);
subplot(5,2,6); plot(real(Rx_x),imag(Rx_x),'go','MarkerFaceColor',[0,1,0]);
axis([-mlevel/2 mlevel/2 -mlevel/2 mlevel/2]);
subplot(5,2,[7 8]); stem(Rx_x_demod(1:50),'filled'); title('Recieved Symbol');
subplot(5,2,[9 10]); stem(Rx_x_BitStream(1:200),'filled'); title('Recieved BitStream');
Review…BER Calculation

45
clear,close,clc all
N=32; % # sub-carriers
x=randi([0 3],1,N); % data in sub-carriers
x1=qammod(x,4); % 4QAM
f=1:N; % sub-carriers freq
t=0:0.001:1-0.001; %synbol duration time
w=2*pi*f.'*t;
%w1=2*pi*(f+0.2).'*t; % sub-carriers
modulation
y1=x1*exp(j*w); % analog mod
x2=ifft(x1,N); % IFFT
plot(t,abs(y1));
hold on;
stem(0:1/N:1-1/N,abs(x2)*N,'-r')
legend('analog modulation','IDFT realization')
title('Compare between analog mod and IDFT')
%x3=fft(x2);
Review…OFDM signal modulation

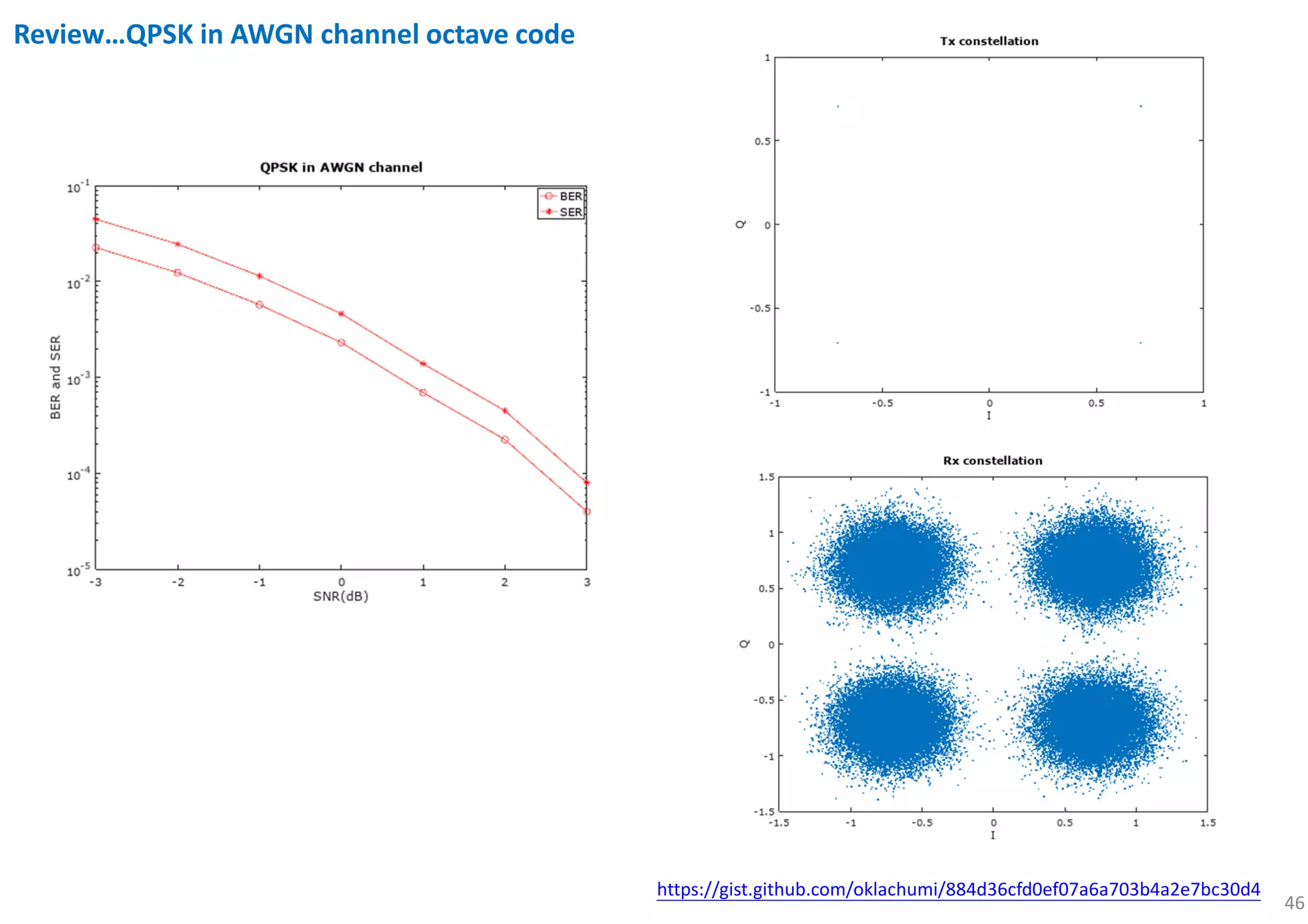
46
Review…QPSK in AWGN channel octave code
https://gist.github.com/oklachumi/884d36cfd0ef07a6a703b4a2e7bc30d4

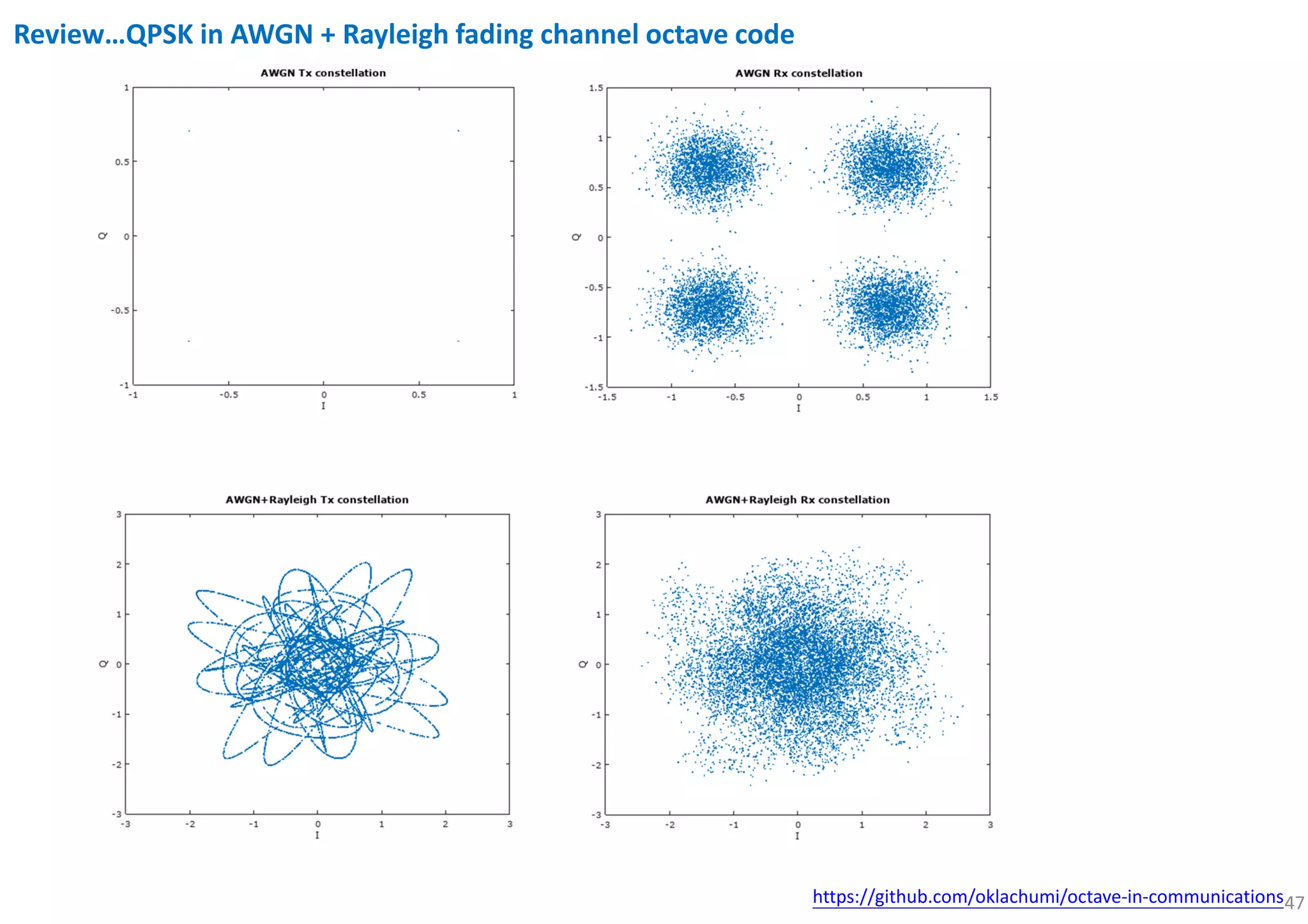
47
Review…QPSK in AWGN + Rayleigh fading channel octave code
https://github.com/oklachumi/octave-in-communications

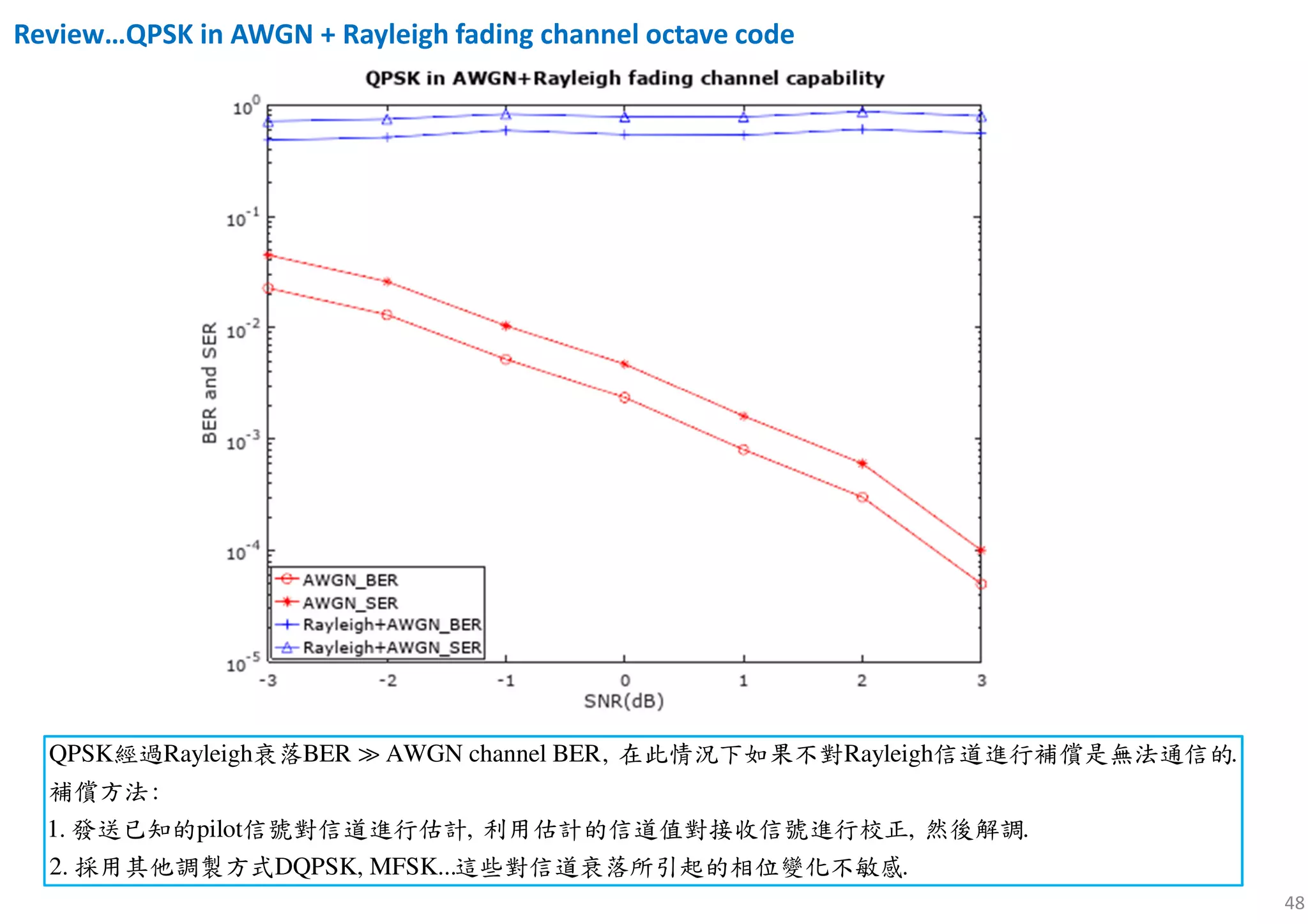
48
Review…QPSK in AWGN + Rayleigh fading channel octave code
QPSK Rayleigh BER AWGN channel BER, Rayleigh .
:
1. pilot , , .
2. DQPSK, MFSK... .
≫經過衰落在此情況下如果不對信道進行補償是無法通信的
補償方法
發送已知的信號對信道進行估計利用估計的信道值對接收信號進行校正然後解調
採用其他調製方式這些對信道衰落所引起的相位變化不敏感

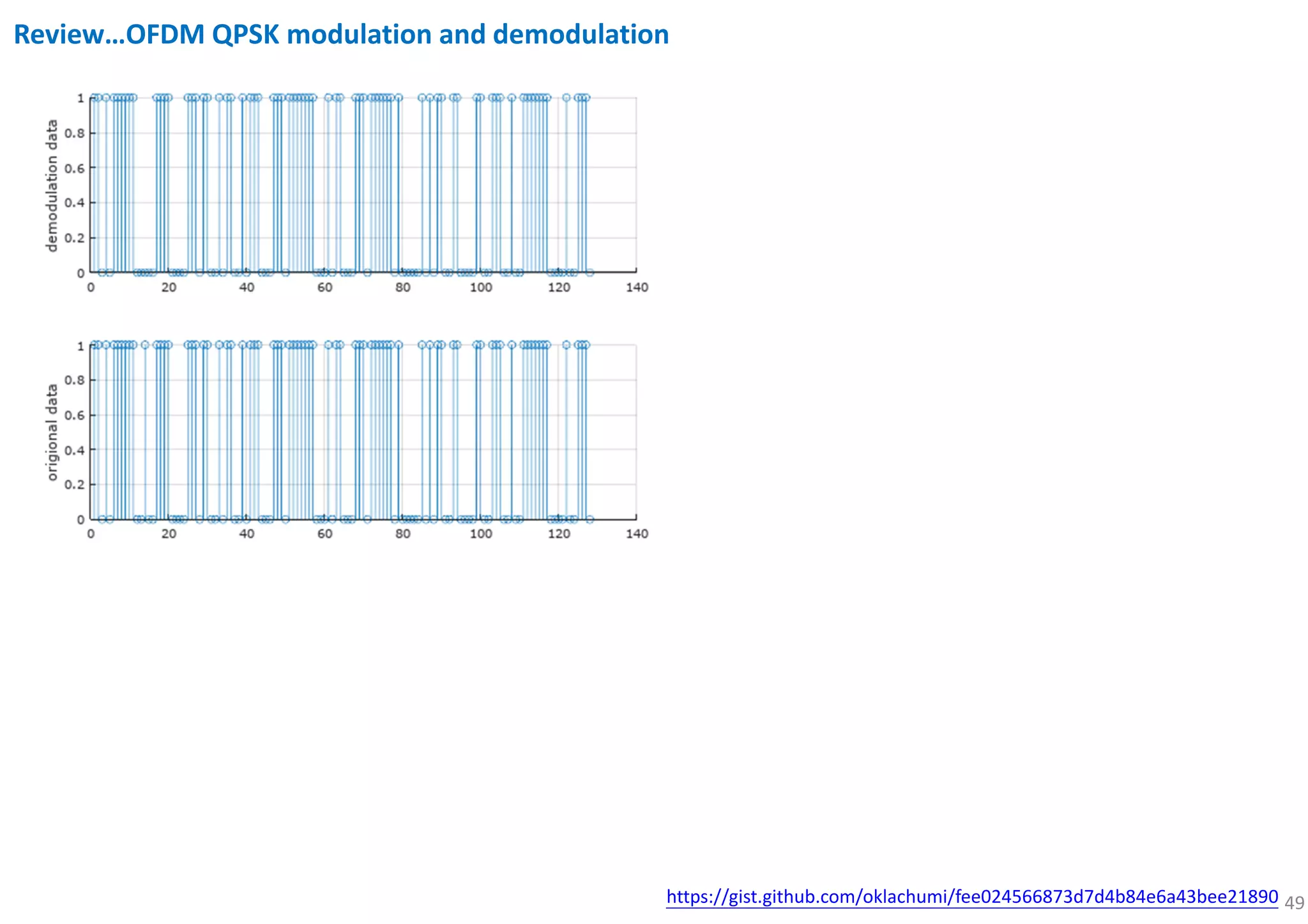
49
Review…OFDM QPSK modulation and demodulation
https://gist.github.com/oklachumi/fee024566873d7d4b84e6a43bee21890

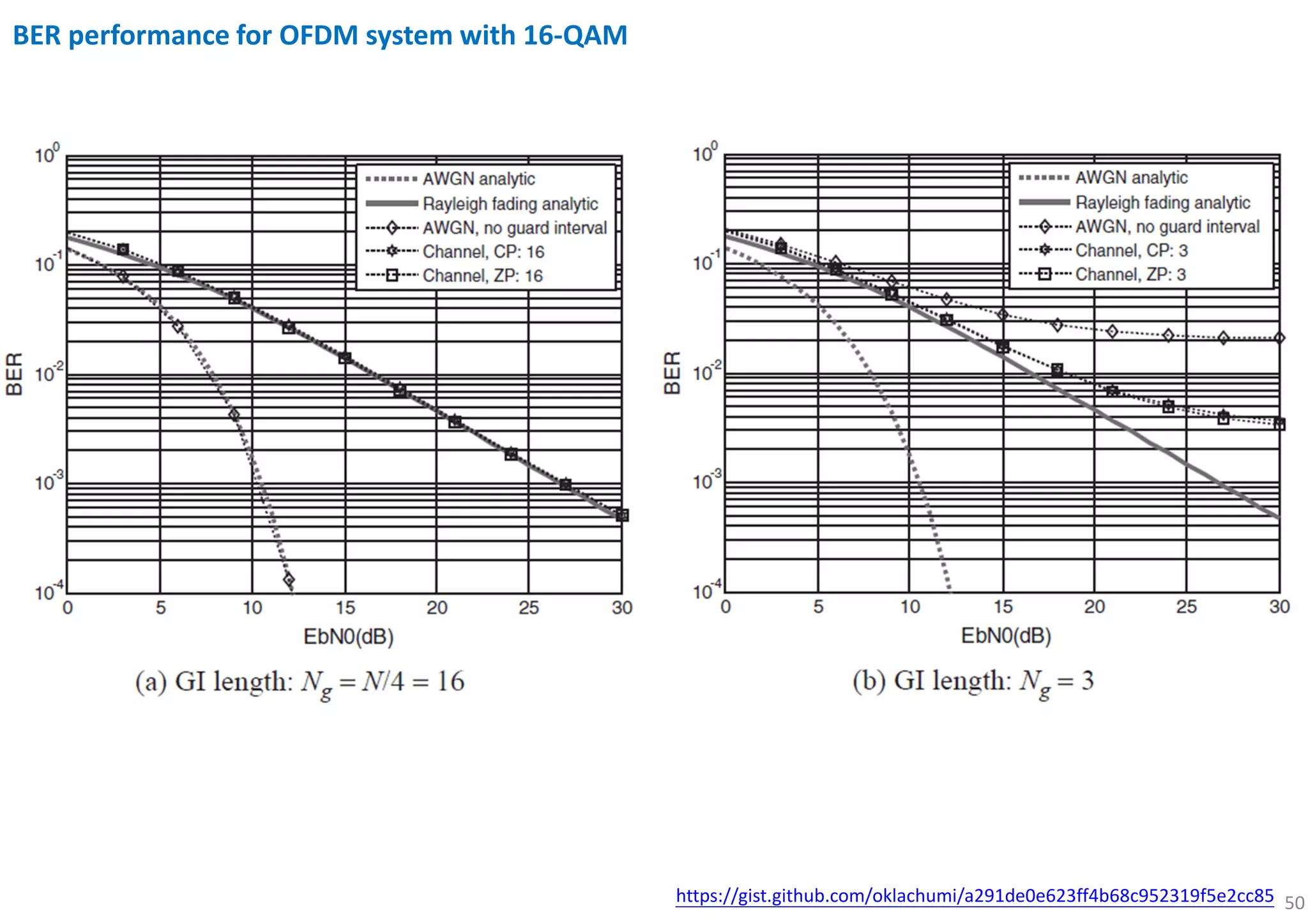
50
BER performance for OFDM system with 16-QAM
https://gist.github.com/oklachumi/a291de0e623ff4b68c952319f5e2cc85

52
Water-Filling Algorithm for Frequency-Domain Link Adaptation
A data rate can be adaptively varied with the channel variation. Such link adaptation is a useful means of maximizing the system
bandwidth efficiency.
One particular example of link adaptation is time-domain AMC (Adaptive Modulation and Coding) technique. It has been widely
adopted for the packet data systems (e.g., cdma2000 1x EV-DO), in which a multiple number of time slots with different channel
gains are dynamically shared among the different users in an opportunistic manner which allows for increasing the average
system throughput.
In addition to time-domain link adaptation, the AMC technique can also be applied to the frequency domain in the OFDM system.
It allows for fully taking advantage of the time-varying characteristics of the subcarriers in the frequency-selective channel for link
adaptation.
The underlying key principle in the frequency-domain AMC technique is the waterfilling (or water pouring) algorithm that
allocates more (or less) bits and power to some subcarriers with larger (or smaller) SNR for maximizing the channel capacity.

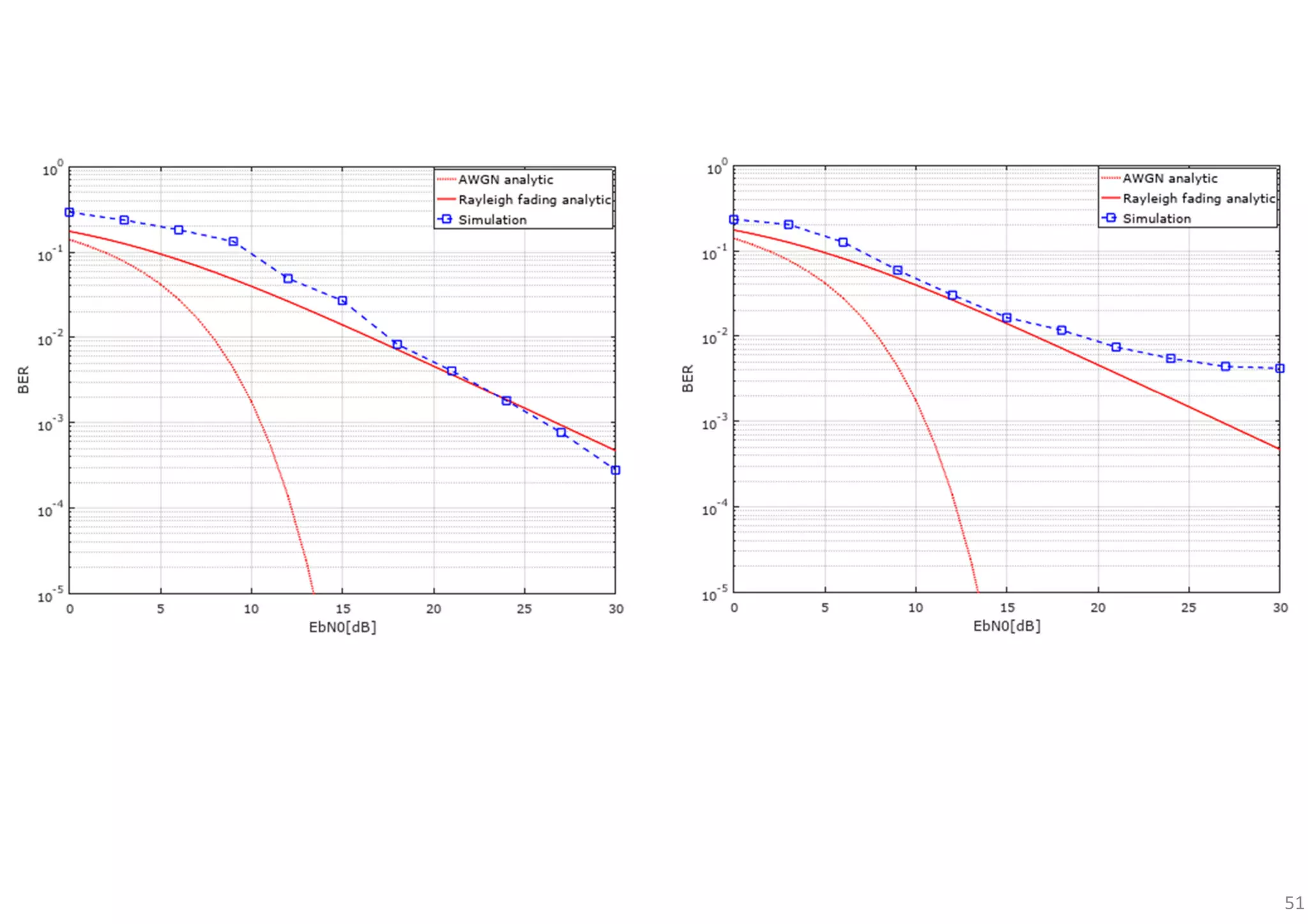
53
coherence BW
, [ ] .
subcarrier, SNR .
f
k H k const
const
∆
⇒ ∀ =
⇒ ∀ =
≪
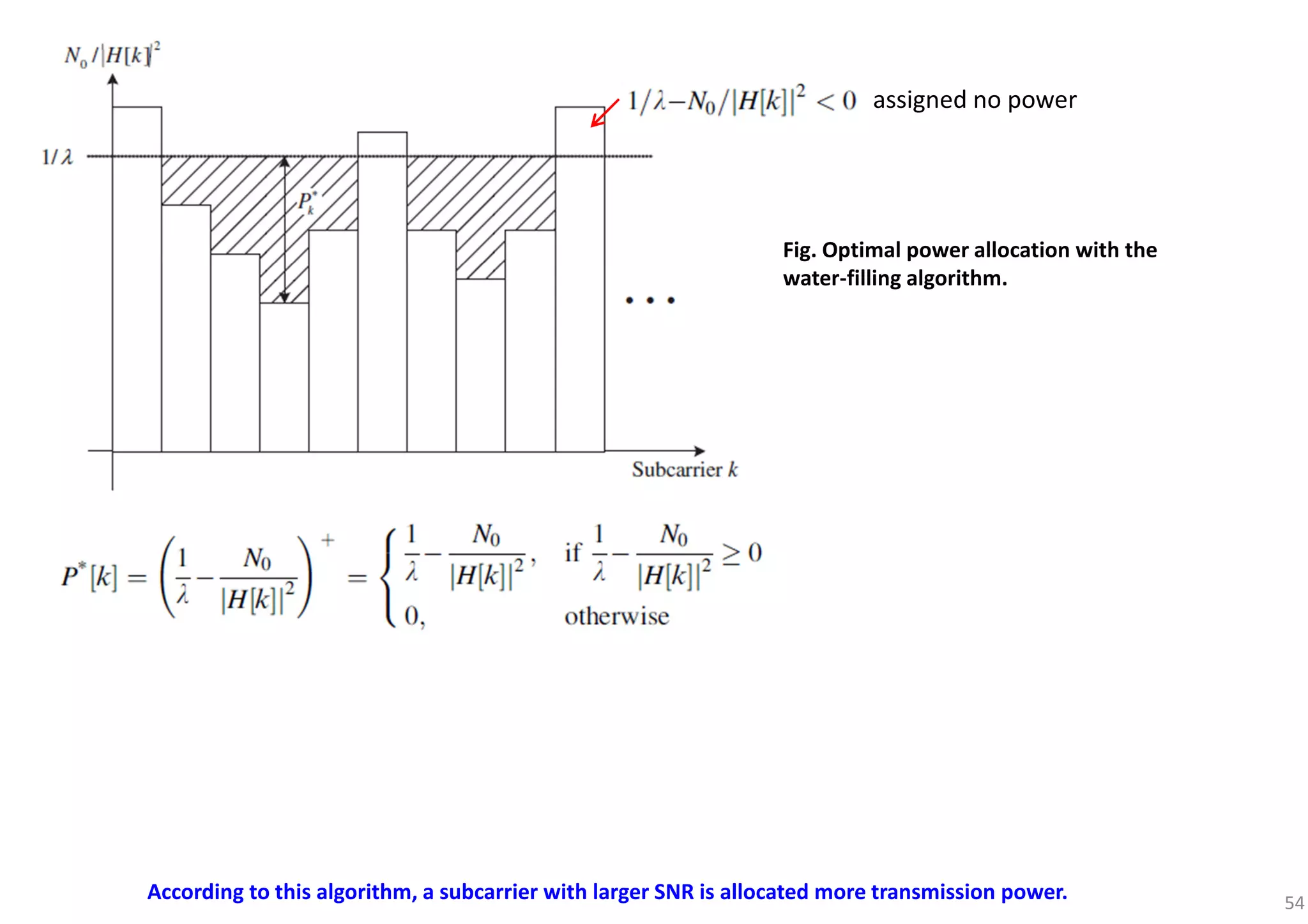
solution implies that the sums of power and NSR (noise-to-signal ratio) for each subcarrier must be the same for all subcarriers
According to this algorithm, a subcarrier with larger SNR is allocated more transmission power.

54
assigned no power
According to this algorithm, a subcarrier with larger SNR is allocated more transmission power.
Fig. Optimal power allocation with the
water-filling algorithm.

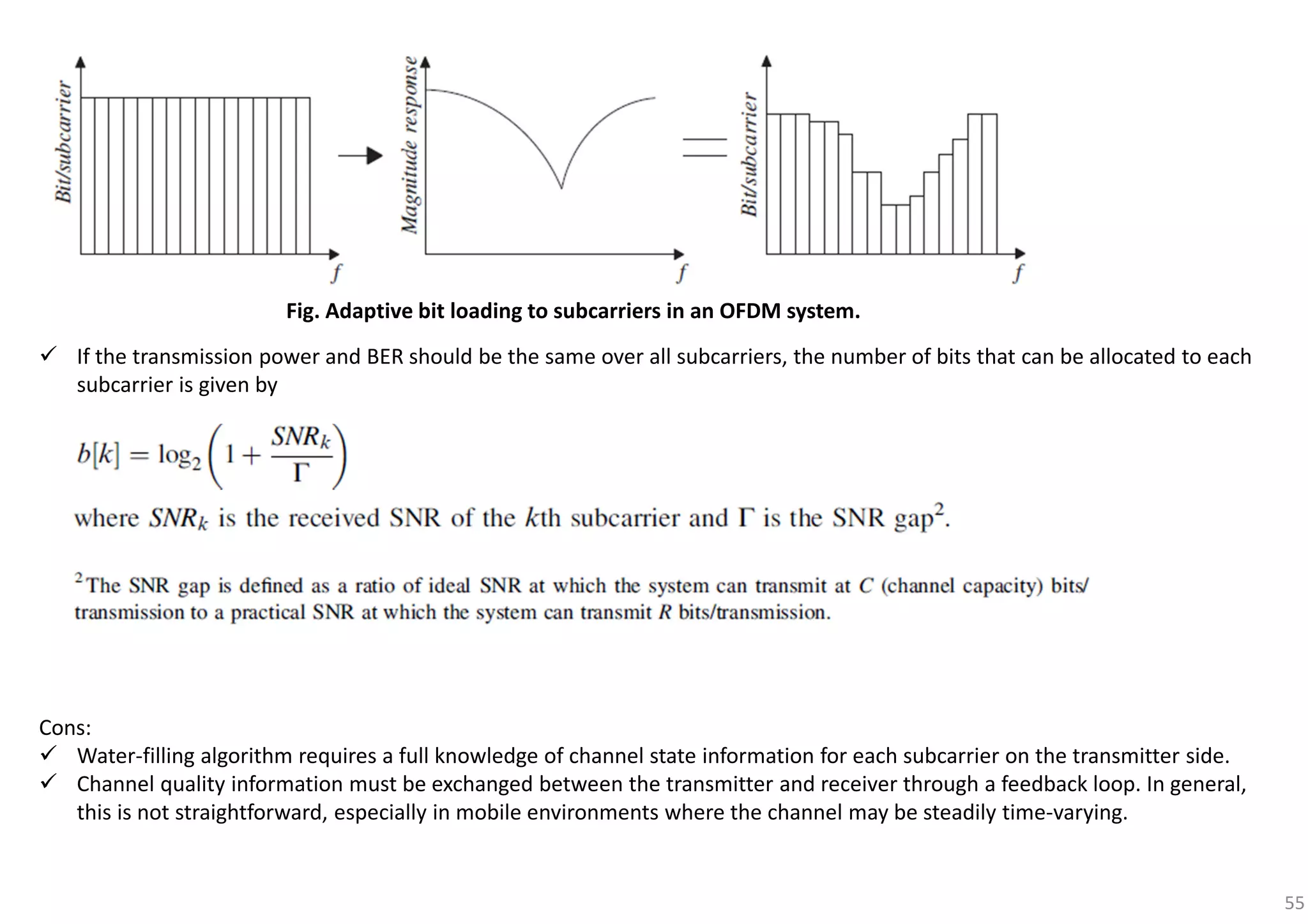
55
Fig. Adaptive bit loading to subcarriers in an OFDM system.
If the transmission power and BER should be the same over all subcarriers, the number of bits that can be allocated to each
subcarrier is given by
Cons:
Water-filling algorithm requires a full knowledge of channel state information for each subcarrier on the transmitter side.
Channel quality information must be exchanged between the transmitter and receiver through a feedback loop. In general,
this is not straightforward, especially in mobile environments where the channel may be steadily time-varying.

56
Coded OFDM
Duplexing
Agenda

57
Coded OFDM
Some consecutive subcarriers in OFDM system suffer from deep fading, in which the received SNR is below the required SNR level.
In order to deal with the burst symbol errors due to deep fading in this multi-carrier situation, it may be essential to employ FEC
(Forward Error Correction) codes.
The popular FEC codes associated with the coded OFDM systems include RS (Reed-Solomon) code, convolutional code, TCM
(Trellis-Coded Modulation), concatenated code, turbo code, and LDPC code.
The FEC codes can make error corrections only as far as the errors are within the error-correcting capability (that is defined as the
maximum number of guaranteed correctable errors per codeword), but they may fail with burst symbol errors.
In practice, interleaving is often employed to convert the burst errors into random errors. There are two types of interleaving:
block interleaving and convolutional interleaving.
Bit-wise, data symbol-wise, or OFDM symbol-wise interleavings can be used for block interleaving.
Interleaving type and size (depth) must be determined by the type of FEC code, degree of frequency and time fading, and delay
due to interleaving.

58
Fig. Example of coded OFDM: Eureka-147-based DAB.
• Figure shows FEC codes and interleaving techniques used in Eureka-147-based DAB (digital audio broadcasting), which
is a typical example of the coded OFDM system.
• Here, concatenated coding is used for FEC.
• An RS code is used for the outer code while TCM is used for the inner code.
• The outer interleaver and inner interleaver are used to separate error bursts from inner coding and to interleave
bits/symbols in the time/frequency domain, respectively.

59
OFDM (Orthogonal Frequency Division Multiplexing)
一種多載波調製技術
較強的抗多徑傳播, 抗頻率選擇性衰落
較高頻譜利用率
單載波單載波單載波單載波調製調製調製調製
將傳輸的data調製到單個載波上進行傳輸
前面介紹的ASK FSK PSK數字調製皆屬於單載波調製
|C(f)
|
t
f
f
B
TB
單單單單載波載波載波載波存在問題存在問題存在問題存在問題
高速data碼元持續時間TB短, 占用帶寬B大
信道特性|C(f)|不理想→碼間串擾ISI
TB < τmax(信道最大多徑延遲差) →產生頻率選擇性衰落, 需複雜的均衡
|C(f)
|

60
NTB
t
f
B/N
多載波調製子多載波調製子多載波調製子多載波調製子信信信信道道道道
頻寬: Bi = B/N < 信道的相干帶寬
碼元持續時間: Ti = NTB > 信道最大多徑時延τmax
資料傳輸速率: Ri = RB/N
|C(f)
|
t
f
f
B
TB
B
TB
多載波多載波多載波多載波調製調製調製調製
將信道分成N個子信道
高速串/並N路低速子數據流
分別調製到各個子載波上並行傳輸
單載波調製單載波調製單載波調製單載波調製多載波調製多載波調製多載波調製多載波調製

61
OFDM多多多多載波載波載波載波調製調製調製調製設計思想設計思想設計思想設計思想
將高速數據流分散調製到多個子載波上並行傳輸
子載波的信號速率大為降低, 子信道均衡也相對容易
∵子信道上的信號帶寬 < 信道的相干帶寬
∴每個子信道上可以看成是平坦衰落, 可消除ISI, 提高抗多徑抗衰落
OFDM的的的的特點特點特點特點:
提高頻譜利用率和增大傳輸速率, 各路子載波的已調信號頻譜有部分重疊
各路已調信號是嚴格正交的, 以便接收端能完全地分離各路信號, ICI↓
每路子載波的調製是多進制調製
每路子載波的調製制度可以不同，根據各個子載波處信道特性的優劣不同採用不同的體制。
並且可以自我調整地改變調製體制以適應信道特性的變化。
OFDM的的的的缺點缺點缺點缺點:
對信道產生的頻率偏移和相位雜訊很敏感
OFDM信號峰值功率和平均功率的比值(PAPR)較大, 這將會降低射頻功率放大器(RFPA)的效率
對同步要求嚴格

62
表表表表達達達達式式式式表表表表達達達達式式式式
設OFDM系統中有N個子信道，每個子信道採用的子載波子載波子載波子載波為：
( ) cos(2 ) 0,1,2 , -1k k k kx t B f t k Nπ φ= + = ⋯
Where Bk 、fk、ϕk －分別為第k路子載波的振幅、頻率、初始相位；
Bk 受基帶碼元的調製。則此系統中的 N 路子信號之和為：
1 1
0 0
( ) ( ) cos(2 )
N N
k k k k
k k
e t x t B f tπ φ
− −
= =
= +∑ ∑＝
可改寫成：
∑
−
=
+
=
1
0
2
B
N
k
tfj
k
kk
ete )(
)( ϕπ
Bk是一個複數, 為第k路子信道中的複輸入資料

63
0
1
{cos[(2 ( ) ] cos[(2 ( ) ]} 0
2
BT
k i k i k i k if f t f f t dtπ φ φ π φ φ− + − + + + + =∫
即
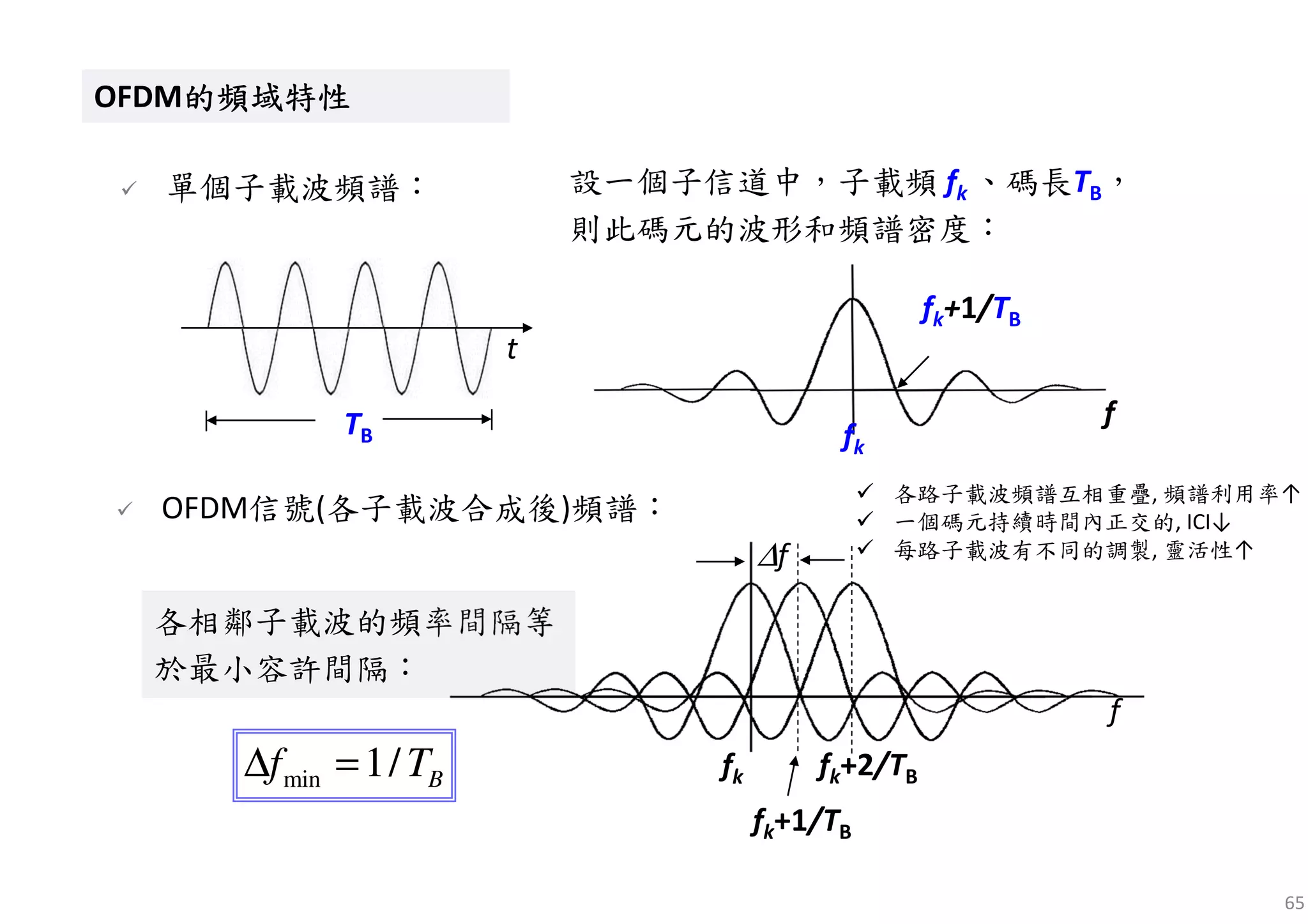
正交條件正交條件正交條件正交條件正交條件正交條件正交條件正交條件
為了使這N路子信道信號在接收時能夠完全分離, 要求它們滿
足正交條件。在TB內, 任意兩個子載波都正交的條件是:
[ ] [ ]
( ) ( )
sin 2 ( ) sin 2 ( )
2 ( ) 2 ( )
sin sin
0
2 ( ) 2 ( )
k i B k i k i B k i
k i k i
k i k i
k i k i
f f T f f T
f f f f
f f f f
π φ φ π φ φ
π π
φ φ φ φ
π π
+ + + − + −
+ −
+ −
+ −
− =
+ −
積分結果為
0
cos(2 )cos(2 ) 0
BT
k k i if t f t dtπ ϕ π ϕ+ + =∫

64
( ) and ( )k i B k i Bf f T m f f T n+ = − =
Where m = 整數和n = 整數；並且ϕk和ϕi可以取任意值
( ) / 2 , ( ) / 2k B i Bf m n T f m n T= + = −
上式等於0的條件：
這就是OFDM子載頻正交的條件子載頻正交的條件子載頻正交的條件子載頻正交的條件
即要求子載頻滿足 fk = k/2TB ，式中 k = 整數；且要求子載頻
間隔∆∆∆∆f = fk – fi = n/TB, 要求的最小子子子子載頻間隔為:
min 1/ Bf T∆ =

65
OFDM的頻域特性的頻域特性的頻域特性的頻域特性OFDM的頻域特性的頻域特性的頻域特性的頻域特性
TB
t
fk+1/TB
fk
f
OFDM信號(各子載波合成後)頻譜：
各相鄰子載波的頻率間隔等
於最小容許間隔：
fk+2/TBfk
∆f
f
fk+1/TB
單個子載波頻譜：設一個子信道中，子載頻 fk 、碼長TB，
則此碼元的波形和頻譜密度：
min 1/ Bf T∆ =
各路子載波頻譜互相重疊, 頻譜利用率↑
一個碼元持續時間內正交的, ICI↓
每路子載波有不同的調製, 靈活性↑

66
OFDM的頻帶利用率的頻帶利用率的頻帶利用率的頻帶利用率OFDM的頻帶利用率的頻帶利用率的頻帶利用率的頻帶利用率
設OFDM系統中共有N 路子載波, 子信道碼元間隔為TB,
每路子載波均採用M 進制的調製, 則佔用的頻帶寬度為
因為一路子信道的位元速率為 OFDM信號N 路的位元速率為
所以OFDM的頻帶利用率為
BOFDM = (N+1) RB

67
2log ( / )OFDM M bps Hzη ≈
當N 很大時
若用單載波的M進制碼元傳輸, 為得到相同的傳輸速率, 則碼元間
隔應縮短為(TB/N)，而佔用頻寬等於(2N/TB)，故頻帶利用率為
∴M-ary single carrier BW = 2Rb∵ Rb = (N/TB)log2M
OFDM和單載波體制相比, 頻帶利用率大約增至2倍

68
直到1971年, S. Weinstein and P. Ebert這兩位老兄提出
• 採用Discrete Fourier Transform (IDFT/DFT)實現多載波調製/解調解決方案
• 取代複雜的硬體結構
• 由於VLSI + DSP, OFDM代表的多載波調製技術實用化!!

69
OFDM的實現：以MQAM調製為例
複習DFT公式
設一個時間信號s(t)的抽樣函數為s(k)，其中k = 0, 1, 2, … , K– 1，
則s(k)的Discrete Fourier Transform (DFT)定義為：
並且S(n)的Inverse Discrete Fourier Transform (IDFT)為:
1
(2 / )
0
1
( ) ( )
K
j K nk
k
S n s k e
K
π
−
−
=
= ∑ )1,,2,1,0( −= Kn ⋯
∑
−
=
=
1
0
)/2(
)(
1
)(
K
n
nkKj
en
K
ks π
S )1,,2,1,0( −= Kk ⋯

70
若信號的抽樣函數s(k)是實函數，則其k點DFT的值S(n)一定滿足對稱性條件：
式中S*(k)是S(k)的複共軛。
令OFDM信號的ϕk＝0，則式
變為
上式和IDFT式非常相似。
若暫時不考慮兩式常數的差異以及求和項數(K和N)的不同則可以將IDFT式中的K個離散
值S(n)當作是K路OFDM並行信號的子信道中信號碼元取值
IDFT式的左端就相當上式左端的OFDM信號s(t)。這就是說，可以用計算IDFT的方法獲得
OFDM信號。
下面就來討論如何具體解決這個計算問題
)(*)1( kkK SS =−− )1,,2,1,0( −= Kk ⋯
1
2
0
( ) k k
N
j f t
k
k
e t e π φ
−
+
=
= ∑B
1
2
0
( ) k
N
j f t
k
k
e t e π
−
=
= ∑B

71
OFDM信號的產生
• 碼元分組：先將輸入碼元序列分成幀，每幀中有F個碼元，即有F比特
• 然後將此F比特分成N組，每組中的比特數可以不同，如下圖所示。
碼元的分組
………
………
t
t
t
B0 B1 B2 B3 BN-1
F比特 F比特 F比特
幀
t
B0
B1
BN-1
b0比特 b1比特 b3比特b2
TB
………
………
Tb
∑
−
=
=
1
0
2
)(
N
k
tfj
k
k
ets π
B
F比特分成N組(0~N-1)

72
設第i組中包含的比特數為bi，則有
將每組中的bi個比特看作是一個Mi進制碼元Bi，其中bi ＝ log2 Mi
並且經過串/並變換將F個串列碼元bi變為N個(路)並行碼元Bi。
各路並行碼元Bi持續時間相同，均為一幀時間TB = F⋅Tb，但是各路碼元Bi包含的比特數不同。
得到的N路並行碼元Bi用來對於N個子載波進行不同的M-QAM調製。
各個碼元Bi可能屬於不同的Mi進制，所以它們各自進行不同的M-QAM調製。
1
0
N
i
i
F b
−
=
= ∑
串/並變換
分幀
分組
串/並
變換
編碼
映射
.
.
.
.
.
.
IDFT .
.
.
並/串
變換
D/A
變換
上
變
頻
OFDM
信號
二進位
輸入信號

1011 1001 1110 1111
1010 1000 1100 1101
0001 0000 0100 0110
0011 0010 0101 0111
A
73
M-QAM調製中一個碼元可以用平面上的一個點表示。
而平面上的一個點可以用一個向量或複數表示。
下面用複數Bi表示此點。將Mi進制的碼元Bi變成一一對應的複數Bi的過程稱為映射過程。
例如，若有一個碼元Bi是16進制的，它由二進位的輸入碼元“1100”構成，則它應進行
16QAM調製。
設其星座圖如下圖所示，則此16進制碼元調製後的相位應該為45°，振幅為A/21/2。此映射
過程就應當將輸入碼元“1100”映射為
( ) /4
/ 2 j
i A e π
=B
分幀
分組
串/並
變換
編碼
映射
.
.
.
.
.
.
IDFT .
.
.
並/串
變換
D/A
變換
上
變
頻
OFDM
信號
二進位
輸入信號

74
用IDFT實現OFDM
1st 令OFDM的最低子載波頻率等於0，以滿足下式
右端第一項(即n = 0時)的指數因數等於1。
為了得到所需的已調信號最終頻位置，可以用上變頻的方法將所得OFDM信號的頻譜
向上搬移到指定的高頻上。
∑
−
=
=
1
0
)/2(
)(
1
)(
K
n
nkKj
en
K
ks π
S )1,,2,1,0( −= Kk ⋯
分幀
分組
串/並
變換
編碼
映射
.
.
.
.
.
.
IDFT .
.
.
並/串
變換
D/A
變換
上
變
頻
OFDM
信號
二進位
輸入信號

75
2nd 我們令K = 2N，使IDFT的項數K等於子信道數目N的2倍，並用對稱性條件:
由N個並行複數碼元序列{Bi}，(其中i = 0, 1, 2, …, N – 1)，生成K＝2N個等效的複數碼元序列
{B’n}，(其中n = 0, 1, 2, …, 2N – 1)，即令{B’n}中的元素等於：
這樣將生成的新碼元序列{B’n}作為S(n)，代入IDFT公式，得到
*
( ) ( )K k k− =S S )1,,2,1,0( −= Kk ⋯
*
1
1 1
0 0
1 2 1 0
, 1, 2, , 1
, , 1, 2, , 2 2
Re( )
Im( )
K n n
K n K n
K N
n N
n N N N N
− −
− − − −
− −
′ = = −
′ = = + + −
′ =
′ ′= =
B B
B B
B B
B B B
⋯
⋯
1
(2 / )
0
1
( )
K
j K nk
n
n
e k e
K
π
−
=
′= ∑B )1,,2,1,0( −= Kk ⋯
分幀
分組
串/並
變換
編碼
映射
.
.
.
.
.
.
IDFT .
.
.
並/串
變換
D/A
變換
上
變
頻
OFDM
信號
二進位
輸入信號
1
(2 / )
0
1
IDFT : ( ) ( )
K
j K nk
n
s k n e
K
π
−
=
= ∑S

76
式中
相當於OFDM信號e(t)的抽樣值。
故e(t)可以表示為
子載波頻率fk = n/TB，(n = 0, 1, 2, … , N - 1)。
離散抽樣信號e(k)經過D/A變換後就得到上式的OFDM信號e(t)。
3rd 進一步克服ISI, 在計算IDFT時加入CP, 在OFDM相鄰碼元間加入保護間隔(GI).
( ) ( / )Be k e kT K=
1
(2 / )
0
1
( )
K
j K nk
n
n
e k e
K
π
−
=
′= ∑B
1
(2 / )
0
1
( ) B
K
j T nt
n
n
e t e
K
π
−
=
′= ∑B (0 )Bt T≤ ≤
分幀
分組
串/並
變換
編碼
映射
.
.
.
.
.
.
IDFT .
.
.
並/串
變換
D/A
變換
上
變
頻
OFDM
信號
二進位
輸入信號

77
OFDM調製原理圖
分幀
分組
串/並
變換
編碼
映射
.
.
.
.
.
.
IDFT .
.
.
並/串
變換
D/A
變換
上
變
頻
OFDM
信號
二進位
輸入信號
0S
1S
1NS −
( ),OFDM RFs t{ }nS
cos2 cf tπ
sin 2 cf tπ−
{ }nb
0OFDMs
1OFDMs
( )1OFDM N
s −
( ),Re OFDM ks
( ),Im OFDM ks

80
For the same BW, the more # of channels, the more rectangular waveform is like.

Introduction to OFDM

More Related Content

What's hot

Similar to Introduction to OFDM

More from Pei-Che Chang

Recently uploaded

Introduction to OFDM