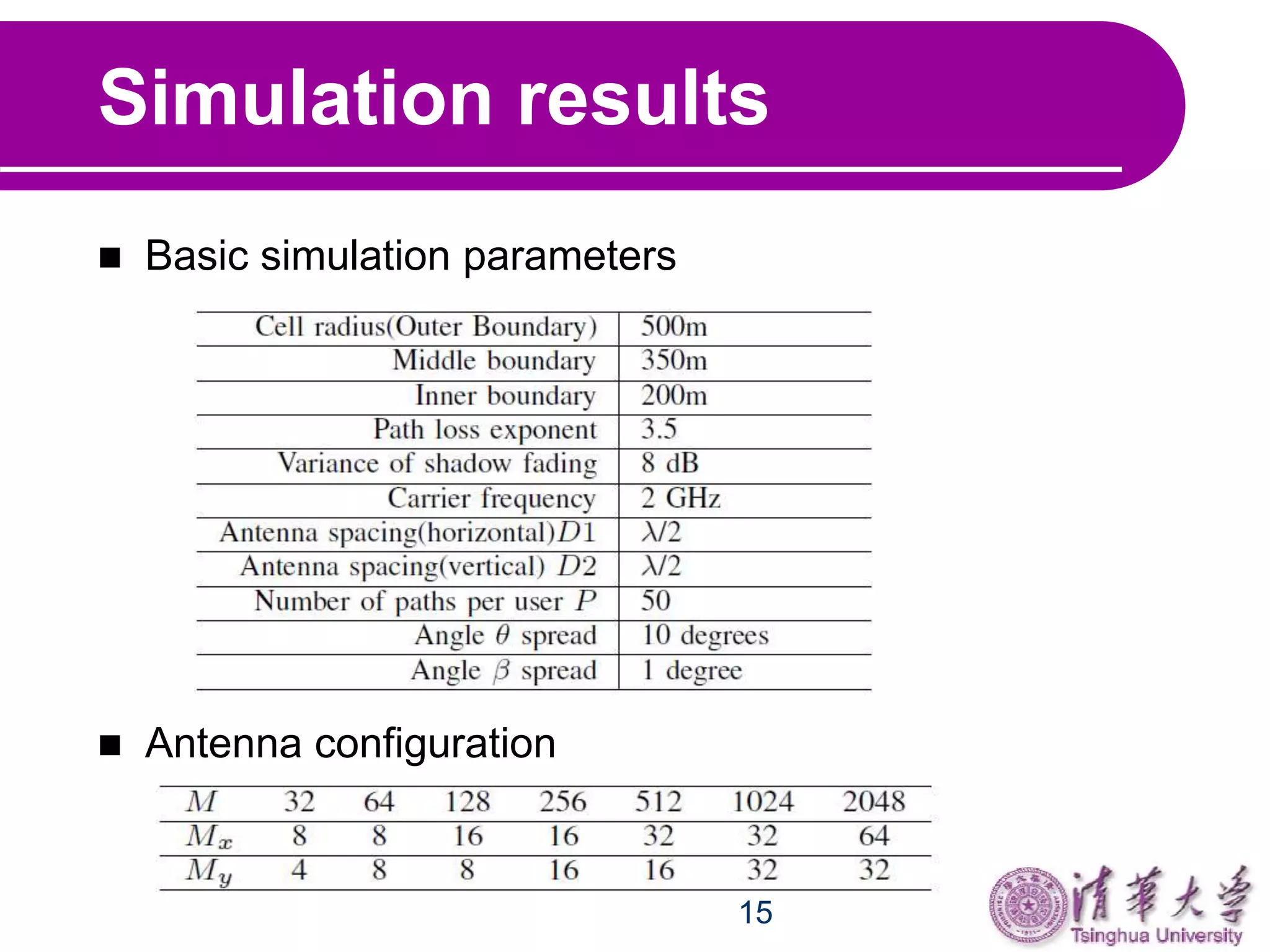
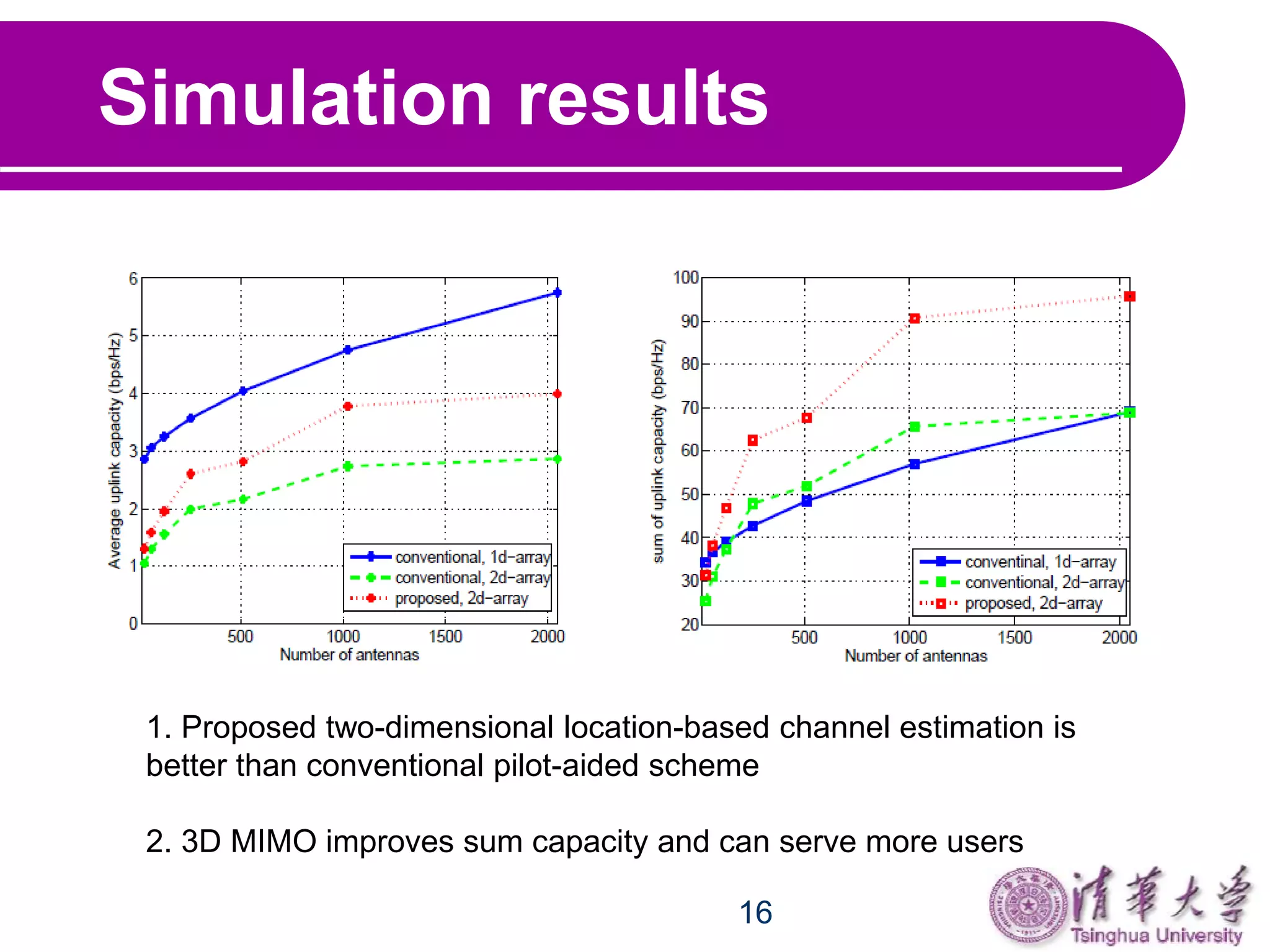
This document proposes a two-dimensional location-based channel estimation method for massive full-dimensional MIMO systems. It uses an intra-cell pilot reuse scheme where users with the same pilots can be distinguished by their unique azimuth and elevation angles of arrival. The method applies a 2D FFT to the pilot-aided channel estimates followed by a 2D window function in the angle domain to isolate the different users. Simulation results show the proposed method outperforms conventional pilot-aided estimation and that 3D MIMO can improve sum capacity and serve more users compared to traditional MIMO systems.

1. Location-based Channel Estimation
for Massive Full-Dimensional MIMO
Systems
Authors: Wendong Liu, Chen Qian and Zhaocheng Wang
Presenter: Qian Han

2. 2
Outline
 Abstract
 Introduction
 System model
 Proposal
 Simulation results
 References

3. 3
Abstract
 Propose a two-dimensional location-based
channel estimation for massive FD-MIMO
systems
 Intra-cell pilot reuse scheme is adopted
 Users with same pilots could be distinguished
by their non-overlapping A-AOAs and E-AOAs
 Interference is reduced and the sum capacity
could be improved

4. 4
Outline
 Abstract
 Introduction
 System model
 Proposal
 Simulation results
 References

5. 5
Introduction
 Massive MIMO is a promising technology for
next generation wireless communication
systems
 Space limitation for large antenna arrays
 FD-MIMO (full-dimensional MIMO, 3D-MIMO)
is proposed and rectangular antenna array
 Massive FD-MIMO systems reach high
capacity

6. 6
Introduction
 With the same number of antennas, ULA perfomrs
better than URA
 More work will focus on optimizing FD-MIMO including
better precoding strategies or elevation beamforming
 A two-dimensional location-based channel estimation
algorithm is proposed with 2D-FFT-based post-
processing is inserted after the conventional pilot-
aided channel estimation

7. 7
Outline
 Abstract
 Introduction
 System model
 Proposal
 Simulation results
 References

8. 8
System model
 A single-cell multi-user FD-MIMO system
 Pilot reuse: 2K users assigned with K orthogonal pilots
 Channel matrix between the l-th user and BS:
 Pilot-aided estimated channel matrix:
 Antenna array size:
 Simplified 3D SCM
Fig. 1 K=12, single-cell pilot reuse pattern
,{ }l l xyhH
lH
y xM M
, , ,
1
1
( , )
P
l l p l p l p
pP
  

 H B
P: number of paths,
: large-scale fading parameter
: A-AOA of the p-th path
: E-AOA of the p-th path
,l p
,l p
,l p
1 p P 

9. 9
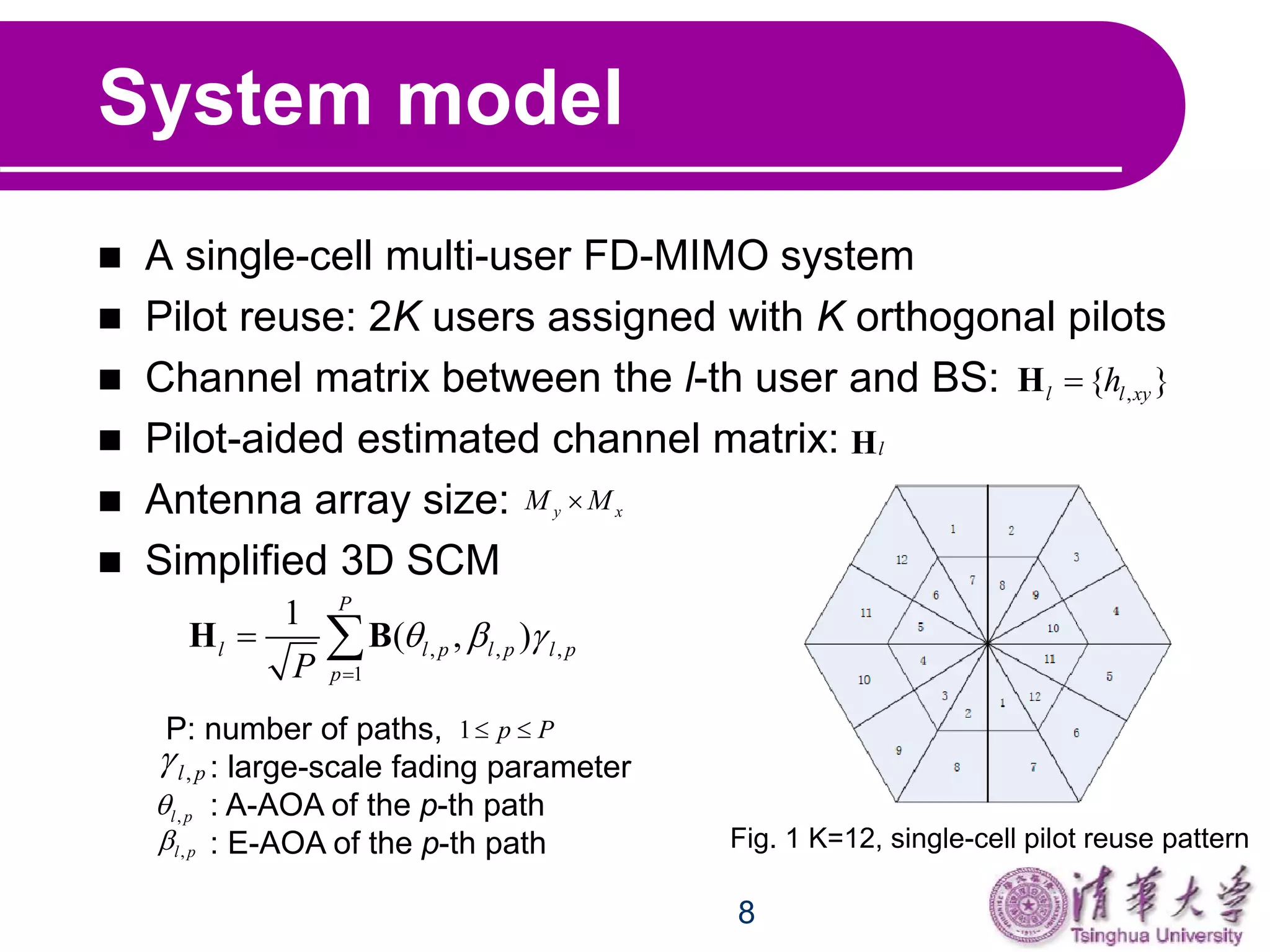
System model
 Steering matrix :
 Assumption: angular spread of A-AOA is small. E-
AOAs are determined by locations of users.
 Inner part user:
 Outer part user:
( , ) { }xyb  B
 cos cos sin
, ( , )
jkD x y
x yb e
  
   

0, 1, 0, 1x yx M y M     
D: antenna spacing, , is the wavelength2 /k   
, min max[ , ]l l
l p  
min max m
arctan ,arctan , arctan ,arctanin out
mid id
L L L L
r r r r
 
   
    
   
min m[ , ]in idd r r
m max[ , ]out idd r r

10. 10
Outline
 Abstract
 Introduction
 System model
 Proposal
 Simulation results
 References

11. 11
Proposal: 2D-DFT Analysis
 Horizontal domain:
 can be seen as a single-frequency signal with
 Vertical domain:
 : single-frequency signal with
 2D-DFT of tends to a 2D- function with infinity
number of antennas. Different users have different
impulse position and could be distinguished in angle
domain.
1 2[ , , , ]y
h h h
M B b b b
cos cos
sin
cos cos
1
y
jkD
h jkDy
y
jkDM
e
e
e
 

 



 
 
 
 
 
  
b
h
yb cos cosh
D
f  


sincos cos sin
1 yjkDMv jkDx jkD
x e e e
    
   b
v
xb sinv
D
f 


B 

12. 12
Proposal: 2D-DFT Analysis
Perform 2D-DFT of :
11
2 ( ) 2 ( )
0 0
11
2 ( ) 2 ( )
0 0
| ( , ) | | || |
| | | |
yx
h h v v
yx
h h v v
MM
j q k j q k
h v
x y
MM
j q k j q k
x y
x y
X k k e e
e e
M M M
 
 

 
 

 
 


  
 
 
Let and( ) cos cosh
x
D k
q k
N
 

  ( ) sinv
y
D k
q k
N


 
( , ) B
| ( , ) |h vX k k reaches maximum value when and both are integers( )hq k( )vq k
( , , )
( , )
h h x
v v y
k g N
k g N
 

    

   
cos cos , [0, )
2
( , , )
cos cos , [ , ]
2
x x
h x
x
D
N N
g N
D
N

  
 

   


 
 
 

min max( , ) sin , [ , ]v y y y
D
g N N N    

  Means rounding operation  

13. 13
Proposal: Procedure
 Calculate the 2D window function in angle domain
 : band-pass rectangle window
 : pilot-aided estimated channel
 : 2D-FFT of : final estimated channel
1,( , )
( , )
0,( , )
h v
I h v
h v
k k I
k k
k k I

 

W
max max min min min max
min min max max
0, ( , , ) ( , , ) , ,0
2
( , , ) , ( , , ) ,
l l l l l l
h x h x x
h
l l l l
h x h x
g N g N N
I
g N g N otherwise

      
   
                
 
        
max min( , ) , ( , )l l
v v y v yI g N g N          
IW
( , )h v
l l I I I h vk k F F W
lH
lF lH
2 ( )(1: ,1: )l l x yIFFT M MH F
lH

14. 14
Outline
 Abstract
 Introduction
 System model
 Proposal
 Simulation results
 References

15. 15
Simulation results
 Basic simulation parameters
 Antenna configuration

16. 16
Simulation results
1. Proposed two-dimensional location-based channel estimation is
better than conventional pilot-aided scheme
2. 3D MIMO improves sum capacity and can serve more users

17. 17
References

18. Thank you and
questions please!