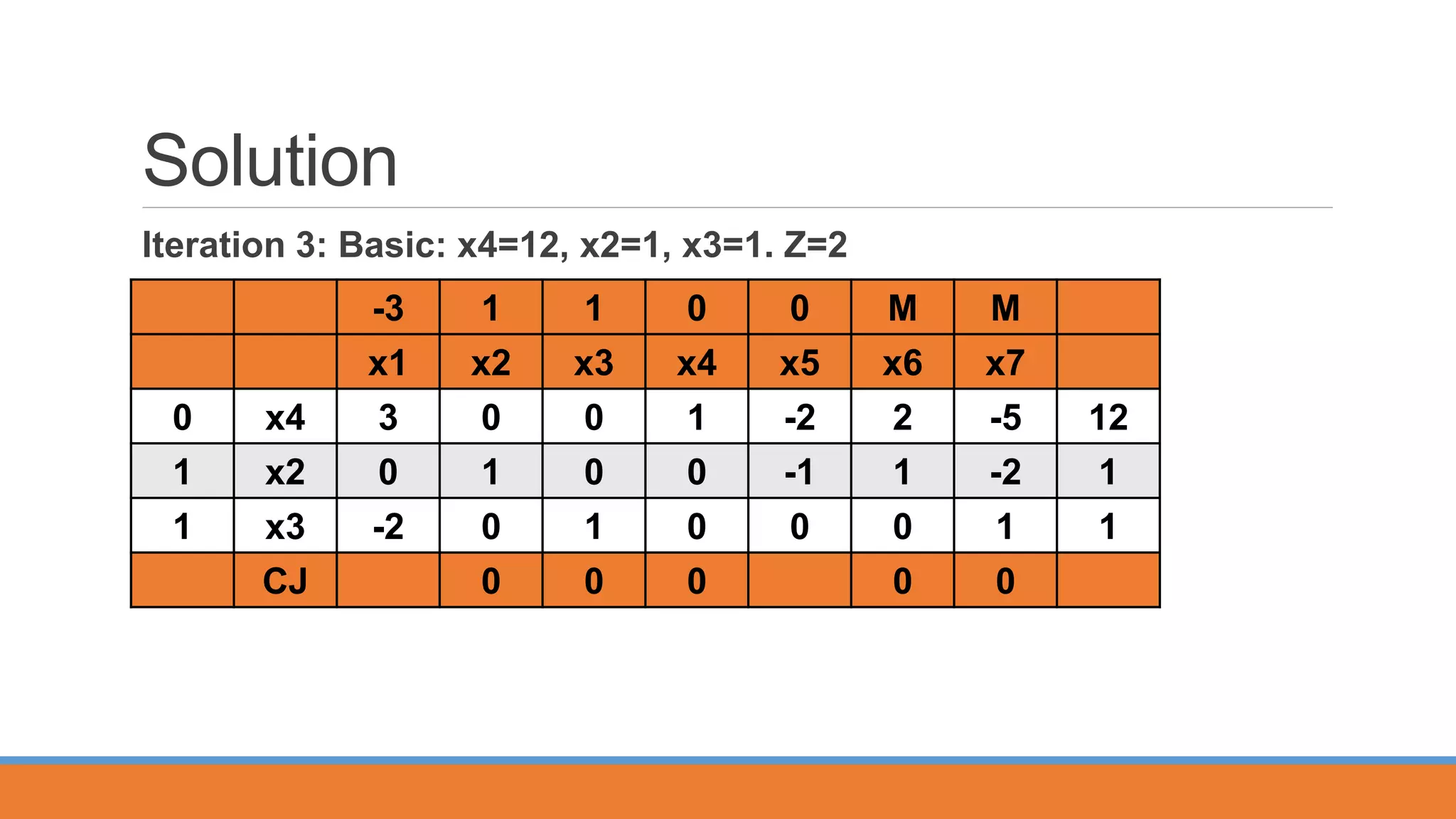
The Big M Method is used to solve linear programming problems with inequality constraints. It involves multiplying inequality constraints to make the right hand side positive, introducing surplus and slack variables, and adding a large penalty term M to the objective for any artificial variables. The example problem is solved using this method in multiple iterations of the simplex algorithm to find the optimal solution.

1. Operations Research
CHAPTER 06 - THE BIG M METHOD

2. The Big M Method
I. Multiply the inequality constraints to ensure that the right hand
side is positive.
II. For any greater-than or equal constraints, introduce surplus and
artificial variables.
III. Choose a large positive M and introduce a term in the objective of
the form M multiplying the artificial variables.
IV. For less-than constraints, introduce slack variables so that all
constraints are equalities.
V. Solve the problem using the usual simplex method.

3. Example
Min Z= -3x1 + x2 + x3
S.T. x1 – 2x2 + x3 <= 11
-4x1+ x2 + 2x3 >= 3
2x1 – x3 = -1

4. Solution
Write the problem in standard form and let the right hand side
positive.
Min Z= -3x1 + x2 + x3
S.T. x1 – 2x2 + x3 + x4 = 11, Slack
-4x1 + x2 +2x3 – x5 = 3, Surplus
-2x1 + x3 = 1

5. Solution
Write the problem in canonical form (add artificial variable to the 2nd
and to the 3rd constraints).
Add M to the artificial variables in the objective function
In case the problem is a maximization problem, add –M as a
coefficient to the artificial variables, Otherwise add M.
Min Z= -3x1 + x2 + x3 + Mx6 + Mx7
S.T. x1 – 2x2 + x3 + x4 = 11
-4x1 + x2 +2x3 – x5 + x6 = 3
-2x1 + x3 + x7 = 1

6. Solution
Iteration 1: Basic: x4=11, x6=3, x7=1. Z=Mx6+Mx7=3M+M=4M
-3 1 1 0 0 M M
x1 x2 x3 x4 x5 x6 x7
0 x4 1 -2 1 1 0 0 0 11
M x6 -4 1 2 0 -1 1 0 3
M x7 -2 0 1 0 0 0 1 1
CJ 0 0 0

7. Solution
C1= -3 – (0,M,M) = 6M-3 >0
C2= 1 – (0,M,M) = 1-M <0
C3= 1 – (0,M,M) = 1-3M <0
C5= 0 – (0,M,M) = M >0
x3 is entering, x3= min{11,3/2,1}=1, x7 is leaving.
1
-4
-2
-2
1
0
1
2
1
0
-1
0

8. Solution
Iteration 2: Basic: x4=11-1=10, x6=3-2=1, x3=1. Z=1+M
-3 1 1 0 0 M M
x1 x2 x3 x4 x5 x6 x7
0 x4 3 -2 0 1 0 0 -1 10
M x6 0 1 0 0 -1 1 -2 1
1 x3 -2 0 1 0 0 0 1 1
CJ 0 0 0 0

9. Solution
C1= -3 – (0,M,1) = -1 <0
C2= 1 – (0,M,1) = 1-M <0
C5= 0 – (0,M,1) = M >0
x2 is entering, x2= min{-5,1,inf.}=1, x6 is leaving.
Basic: x4=12, x2=1, x3=1. Z=2.
3
0
-2
-2
1
0
0
-1
0

10. Solution
Iteration 3: Basic: x4=12, x2=1, x3=1. Z=2
-3 1 1 0 0 M M
x1 x2 x3 x4 x5 x6 x7
0 x4 3 0 0 1 -2 2 -5 12
1 x2 0 1 0 0 -1 1 -2 1
1 x3 -2 0 1 0 0 0 1 1
CJ 0 0 0 0 0

11. Solution
C1= -3 – (0,1,1) = -1 <0
C5= 0 – (0,1,1) = 1 >0
x1 is entering, x1= min{4,inf.,-1/2}=4, x4 is leaving.
Basic: x1=4, x2=1, x3=9. Z=-2.
3
0
-2
-2
-1
0

12. Solution
Iteration 4: Basic: x1=4, x2=1, x3=9. Z=-2
-3 1 1 0 0 M M
x1 x2 x3 x4 x5 x6 x7
-3 x1 1 0 0 1/3 -2/3 2/3 -5/3 4
1 x2 0 1 0 0 -1 1 -2 1
1 x3 0 0 1 2/3 -4/3 4/3 -7/3 9
CJ 0 0 0 0 0 0

13. Solution
C5= 0 – (-3,1,1) = 1/3 >0
No entering variables.
The current solution is optimal.
x1=4, x2=1, x3=9, Z=-2
-2/3
-1
-4/3

14. Example 2
Max Z= x1 + 2x2 + x3
S.T. x1 + x2 + x3 = 7
2x1 – 5x2 +x3 >= 10
In standard form: Max Z= x1 + 2x2 + x3
S.T. x1 + x2 + x3 = 7
2x1 – 5x2 +x3 – x4 = 10
In chanocial form: Max Z= x1 + 2x2 + x3 – Mx5 – Mx6 (Minus cuz its
max
S.T. x1 + x2 + x3 + x5 = 7
2x1 – 5x2 +x3 – x4 + x6 = 10

15. Solution
Iteration 1: Basic: x5=7, x6=10. Z=-17M
1 2 1 0 -M -M
x1 x2 x3 x4 x5 x6
-M x5 1 1 1 0 1 0 7
-M x6 2 -5 1 -1 0 1 10
CJ 0 0 -
17M

16. Solution
C1= 1 – (-M,-M) = 1+3M
C2= 2 – (-M,-M) = 2-4M
C3= 1 – (-M,-M) = 1+2M
C4= 0 – (-M,-M) = -M
x1 is entering, x1= min{7,5}=5, x6 is leaving.
1
2
1
-5
1
1
0
-1

17. Solution
Iteration 2: Basic: x5=2, x1=5. Z=5-2M
1 2 1 0 -M -M
x1 x2 x3 x4 x5 x6
-M x5 0 7/2 1/2 1/2 1 -1/2 2
1 x1 1 -5/2 1/2 -1/2 0 1/2 5
CJ 0 0 0

18. Solution
C2= 2 – (-M,1 ) = (9+7M)/2
C3= 1 – (-M,1 ) = (1+M)/2
C4= 0 – (-M,1 ) = (1+M)/2
x2 is entering, x2= min{4/7,-2}=4/7, x5 is leaving.
7/2
-5/2
1/2
1/2
1/2
-1/2

19. Solution
Iteration 3: Basic: x2=4/7, x1=45/7. Z=53/7
1 2 1 0 -M -M
x1 x2 x3 x4 x5 x6
2 x2 0 1 1/7 1/7 2/7 -1/7 4/7
1 x1 1 0 6/7 -1/7 5/7 1/7 45/7
CJ 0 0 0 0 53/7

20. Solution
C3= 1 – ( 2,1 ) = -1/7
C4= 0 – ( 2,1 ) = -1/7
No entering variables, the current solution is optimal.
x2=4/7, x1=45/7, z= 53/7
1/7
6/7
1/7
-1/7

21. Example of unrestricted variables
Min Z= 3x1 + 2x2 + x3
S.T. 2x1 + 5x2 + x3 = 12
3x1+ 4x2 = 11
x2,x3 >=0, x1 is unrestricted
x1= x1’ – x1’’

22. Example of unrestricted variables
Min Z= 3x1’ – 3x1’’ + 2x2 + x3 + Mx4 + Mx5
S.T. 2x1’ – 2x1’’ + 5x2 + x3 + x4 = 12
3x1’ – 3x1’’ + 4x2 + x5 = 11
x1’, x1’’, x2, x3 >=0

23. Solution
Iteration 1: Basic: x4=12, x5=11. Z=-Mx4-Mx5=23M
X2 is entering and its equal to min{12/5,11/4}=12/5, so x4 is leaving
ZJ is obtained by adding the products of the elements under that
column with the corresponding CB values (the first column: 2M+3M)
CJ 3 -3 2 1 M M
CB Basis x1’ x1’’ x2 x3 x4 x5
M x4 2 -2 5 1 1 0 12
M x5 3 -3 4 0 0 1 11
ZJ 5M -5M 9M M M M 23M
CJ-ZJ 3-5M -3+5M 2-9M 1-M 0 0

24. Solution
Iteration 2: Basic: x2 and x5
X1’ is entering and its equal to min{6,1}=1, so x5 is leaving
CJ 3 -3 2 1 M M
C
B
Basi
s
x1’ x1’’ x2 x3 x4 x5
2 x2 2/5 -2/5 1 1/5 1/5 0 12/5
M x5 7/5 -7/5 0 -4/5 -4/5 1 7/5
ZJ 4/5-7/5M -4/5+7/5M 2 2/5+4/5M 2/5+4/5M -M 24/5-7/5M
CJ-
ZJ
11/5-7/5M -11/5+7/5M 0 3/5+4/5M 9/5M-2/5 0

25. Solution
Iteration 1: Basic: x1’ and x2.
X3 is entering and its equal to min{14/3,-7/4}=14/3, so x2 is leaving
CJ 3 -3 2 1 M M
CB Basis x1’ x1’’ x2 x3 x4 x5
2 x2 0 0 1 3/7 3/7 -2/7 2
3 x1’ 1 -1 0 -4/7 -4/7 5/7 1
ZJ 3 -3 2 -6/7 -6/7 11/7 7
CJ-
ZJ
0 0 0 13/7 -M+6/7 -M-11/7

26. Solution
Iteration 1: Basic: x4=12, x5=11. Z=-Mx4-Mx5=-23M
No entering variables so the solution is optimal
CJ 3 -3 2 1 -M -M
CB Basis x1’ x1’’ x2 x3 x4 x5
1 x3 0 0 7/3 1 1 -2/3 14/3
3 x1’ 1 -1 4/3 0 0 1/3 11/3
ZJ 3 -3 19/3 1 1 -2/3 1
CJ-
ZJ
0 0 -13/3 0 -M-1 -M-1/3