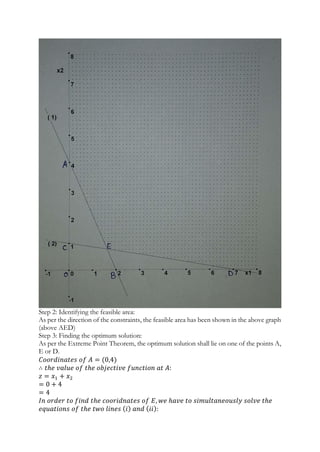
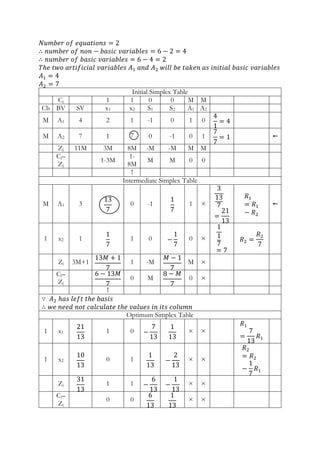
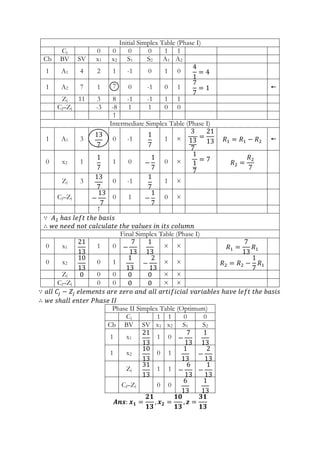
The document presents a two-phase method for solving a linear programming problem (LPP), specifically minimizing the objective function z=x1+x2 under certain constraints. It details the graphical method to identify feasible regions and optimal solutions, including the use of simplex tables for calculations. Additionally, it outlines steps for introducing surplus and artificial variables to convert inequalities into equalities for further analysis.

1. Two-Phase Method of solving an LPP
Solve the following problem by using Two-Phase method (2018, 7 marks)
Minimize z=x1+x2
subject to 2x1+x2≥4,
x1+7x2≥7,
and x1, x2≥0
Graphical Method
Step 1: Plotting the graph
𝑇𝑎𝑘𝑖𝑛𝑔 𝑡ℎ𝑒 𝑡𝑤𝑜 𝑒𝑥𝑝𝑙𝑖𝑐𝑖𝑡 𝑐𝑜𝑛𝑠𝑡𝑟𝑎𝑖𝑛𝑡𝑠 𝑎𝑠 𝑒𝑞𝑢𝑎𝑙𝑖𝑡𝑖𝑒𝑠:
2𝑥1 + 𝑥2 = 4 … (𝑖)
𝑥1 + 7𝑥2 = 7 … ( 𝑖𝑖)
𝐼𝑛 𝑜𝑟𝑑𝑒𝑟 𝑡𝑜 𝑝𝑙𝑜𝑡 𝑡ℎ𝑒 𝑙𝑖𝑛𝑒𝑠 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑒𝑑 𝑏𝑦 𝑡ℎ𝑒𝑠𝑒 𝑡𝑤𝑜 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛𝑠, 𝑤𝑒 𝑛𝑒𝑒𝑑 𝑡𝑤𝑜
𝑝𝑜𝑖𝑛𝑡𝑠 𝑒𝑎𝑐ℎ, 𝑡ℎ𝑟𝑜𝑢𝑔ℎ 𝑤ℎ𝑖𝑐ℎ 𝑡ℎ𝑒𝑦 𝑝𝑎𝑠𝑠.
𝐼𝑛 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 ( 𝑖):
𝐿𝑒𝑡 𝑥1 = 0
𝑇ℎ𝑒𝑛
2 × 0 + 𝑥2 = 4
𝑜𝑟 0 + 𝑥2 = 4
∴ 𝑥2 = 4
∴ 𝑓𝑖𝑟𝑠𝑡 𝑝𝑜𝑖𝑛𝑡 = (0,4)
𝑁𝑒𝑥𝑡, 𝑙𝑒𝑡 𝑥2 = 0
𝑇ℎ𝑒𝑛
2𝑥1 + 0 = 4
𝑜𝑟 2𝑥1 = 4
𝑜𝑟 𝑥1 =
4
2
∴ 𝑥1 = 2
∴ 𝑠𝑒𝑐𝑜𝑛𝑑 𝑝𝑜𝑖𝑛𝑡 = (2,0)
𝐼𝑛 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 ( 𝑖𝑖):
𝐿𝑒𝑡 𝑥1 = 0
𝑇ℎ𝑒𝑛
0 + 7𝑥2 = 7
𝑜𝑟 7𝑥2 = 7
𝑜𝑟 𝑥2 =
7
7
∴ 𝑥2 = 1
∴ 𝑓𝑖𝑟𝑠𝑡 𝑝𝑜𝑖𝑛𝑡 = (0,1)
𝑁𝑒𝑥𝑡, 𝑙𝑒𝑡 𝑥2 = 0
𝑇ℎ𝑒𝑛
𝑥1 + 7 × 0 = 7
𝑜𝑟 𝑥1 + 0 = 7
∴ 𝑥1 = 7
∴ 𝑠𝑒𝑐𝑜𝑛𝑑 𝑝𝑜𝑖𝑛𝑡 = (7,0)
𝑇ℎ𝑒 𝑔𝑟𝑎𝑝ℎ:

2. Step 2: Identifying the feasible area:
As per the direction of the constraints, the feasible area has been shown in the above graph
(above AED)
Step 3: Finding the optimum solution:
As per the Extreme Point Theorem, the optimum solution shall lie on one of the points A,
E or D.
𝐶𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠 𝑜𝑓 𝐴 = (0,4)
∴ 𝑡ℎ𝑒 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑡ℎ𝑒 𝑜𝑏𝑗𝑒𝑐𝑡𝑖𝑣𝑒 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑎𝑡 𝐴:
𝑧 = 𝑥1 + 𝑥2
= 0 + 4
= 4
𝐼𝑛 𝑜𝑟𝑑𝑒𝑟 𝑡𝑜 𝑓𝑖𝑛𝑑 𝑡ℎ𝑒 𝑐𝑜𝑜𝑟𝑖𝑑𝑛𝑎𝑡𝑒𝑠 𝑜𝑓 𝐸, 𝑤𝑒 ℎ𝑎𝑣𝑒 𝑡𝑜 𝑠𝑖𝑚𝑢𝑙𝑡𝑎𝑛𝑒𝑜𝑢𝑠𝑙𝑦 𝑠𝑜𝑙𝑣𝑒 𝑡ℎ𝑒
𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑡𝑤𝑜 𝑙𝑖𝑛𝑒𝑠 ( 𝑖) 𝑎𝑛𝑑 ( 𝑖𝑖):

3. 2𝑥1 + 𝑥2 = 4 … (𝑖)
𝑥1 + 7𝑥2 = 7 … ( 𝑖𝑖)
𝑀𝑢𝑙𝑡𝑖𝑝𝑙𝑦𝑖𝑛𝑔 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 ( 𝑖𝑖) 𝑏𝑦 2 𝑎𝑛𝑑 𝑠𝑢𝑏𝑡𝑟𝑎𝑐𝑡𝑖𝑛𝑔 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 ( 𝑖) 𝑓𝑟𝑜𝑚 𝑖𝑡:
2𝑥1 + 14𝑥2 = 14
2𝑥1 + 𝑥2 = 4
− − −
0 + 13𝑥2 = 10̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅
𝑜𝑟 13𝑥2 = 10
𝑜𝑟 𝑥2 =
10
13
𝑆𝑢𝑏𝑠𝑡𝑖𝑡𝑢𝑡𝑖𝑛𝑔 𝑡ℎ𝑖𝑠 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑥2 𝑖𝑛 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 ( 𝑖𝑖):
𝑥1 + 7 ×
10
13
= 7
𝑜𝑟 𝑥1 +
70
13
= 7
𝑜𝑟 𝑥1 = 7 −
70
13
=
13 × 7 − 70
13
=
91 − 70
13
=
21
13
∴ 𝑐𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠 𝑜𝑓 𝐸 = (
21
13
,
10
13
)
∴ 𝑡ℎ𝑒 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑡ℎ𝑒 𝑜𝑏𝑗𝑒𝑐𝑡𝑖𝑣𝑒 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑎𝑡 𝐸:
𝑧 = 𝑥1 + 𝑥2 =
21
13
+
10
13
=
31
13
= 2
5
13
𝐶𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠 𝑜𝑓 𝐷 = (7,0)
∴ 𝑡ℎ𝑒 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑡ℎ𝑒 𝑜𝑏𝑗𝑒𝑐𝑡𝑖𝑣𝑒 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑎𝑡 𝐷:
𝑧 = 𝑥1 + 𝑥2
= 7 + 0
= 7
∵ 𝑡ℎ𝑒 𝑜𝑏𝑗𝑒𝑐𝑡𝑖𝑣𝑒 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑖𝑠 𝑜𝑓 𝑚𝑖𝑛𝑖𝑚𝑖𝑠𝑎𝑡𝑖𝑜𝑛 𝑡𝑦𝑝𝑒
∴ 𝑡ℎ𝑒 𝑜𝑝𝑡𝑖𝑚𝑢𝑚 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑧 = 𝑡ℎ𝑒 𝑚𝑖𝑛𝑖𝑚𝑢𝑚 𝑝𝑜𝑠𝑠𝑖𝑏𝑙𝑒 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑧 = 2
5
13
𝑨𝒏𝒔: 𝑻𝒉𝒆 𝒎𝒊𝒏𝒊𝒎𝒖𝒎 𝒗𝒂𝒍𝒖𝒆 𝒐𝒇 𝒛 𝒊𝒔 𝟐
𝟓
𝟏𝟑
𝒇𝒐𝒓 𝒙 𝟏 𝒆𝒒𝒖𝒂𝒍 𝒕𝒐
𝟐𝟏
𝟏𝟑
𝒂𝒏𝒅 𝒙 𝟐 𝒆𝒒𝒖𝒂𝒍 𝒕𝒐
𝟏𝟎
𝟏𝟑
Simplex Method
𝐼𝑛𝑡𝑟𝑜𝑑𝑢𝑐𝑖𝑛𝑔 𝑠𝑢𝑟𝑝𝑙𝑢𝑠 𝑎𝑛𝑑 𝑎𝑟𝑡𝑖𝑓𝑖𝑐𝑖𝑎𝑙 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠:
𝑀𝑖𝑛𝑖𝑚𝑖𝑠𝑒 𝑧 = 𝑥1 + 𝑥2 + 0𝑆1 + 0𝑆2 + 𝑀𝐴1 + 𝑀𝐴2
𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜:
2𝑥1 + 𝑥2 − 𝑆1 + 𝐴1 = 4 … (𝑖)
𝑥1 + 7𝑥2 − 𝑆2 + 𝐴2 = 7 … (𝑖𝑖)
𝑥1, 𝑥2, 𝑆1, 𝑆2, 𝐴1, 𝐴2 ≥ 0
𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 = 6

4. 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛𝑠 = 2
∴ 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑛𝑜𝑛 − 𝑏𝑎𝑠𝑖𝑐 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 = 6 − 2 = 4
∴ 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑠𝑖𝑐 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 = 6 − 4 = 2
𝑇ℎ𝑒 𝑡𝑤𝑜 𝑎𝑟𝑡𝑖𝑓𝑖𝑐𝑖𝑎𝑙 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 𝐴1 𝑎𝑛𝑑 𝐴2 𝑤𝑖𝑙𝑙 𝑏𝑒 𝑡𝑎𝑘𝑒𝑛 𝑎𝑠 𝑖𝑛𝑖𝑡𝑖𝑎𝑙 𝑏𝑎𝑠𝑖𝑐 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠
𝐴1 = 4
𝐴2 = 7
Initial Simplex Table
Cj 1 1 0 0 M M
Cb BV SV x1 x2 S1 S2 A1 A2
M A1 4 2 1 -1 0 1 0
4
1
= 4
M A2 7 1 7 0 -1 0 1
7
7
= 1 
Zj 11M 3M 8M -M -M M M
Cj–
Zj
1-3M
1-
8M
M M 0 0

Intermediate Simplex Table
M A1 3
13
7
0 -1
1
7
1 ×
3
13
7
=
21
13
𝑅1
= 𝑅1
− 𝑅2

1 x2 1
1
7
1 0 −
1
7
0 ×
1
1
7
= 7
𝑅2 =
𝑅2
7
Zj 3M+1
13𝑀 + 1
7
1 -M
𝑀 − 1
7
M ×
Cj–
Zj
6 − 13𝑀
7
0 M
8 − 𝑀
7
0 ×

∵ 𝐴2 ℎ𝑎𝑠 𝑙𝑒𝑓𝑡 𝑡ℎ𝑒 𝑏𝑎𝑠𝑖𝑠
∴ 𝑤𝑒 𝑛𝑒𝑒𝑑 𝑛𝑜𝑡 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒 𝑡ℎ𝑒 𝑣𝑎𝑙𝑢𝑒𝑠 𝑖𝑛 𝑖𝑡𝑠 𝑐𝑜𝑙𝑢𝑚𝑛
Optimum Simplex Table
1 x1
21
13
1 0 −
7
13
1
13
× ×
𝑅1
=
7
13
𝑅1
1 x2
10
13
0 1
1
13
−
2
13
× ×
𝑅2
= 𝑅2
−
1
7
𝑅1
Zj
31
13
1 1 −
6
13
−
1
13
× ×
Cj–
Zj
0 0
6
13
1
13
× ×

5. 𝑨𝒏𝒔: 𝒙 𝟏 =
𝟐𝟏
𝟏𝟑
, 𝒙 𝟐 =
𝟏𝟎
𝟏𝟑
, 𝒛 =
𝟑𝟏
𝟏𝟑
Two-Phase Method
Here the solution of the LPP is completed in two phases. In the first phase of the method,
the sum of the artificial variables is minimised subject to the given constraints to get a basic
feasible solution. Th second phase minimises the original objective function starting with
the basic feasible solution obtained at the end of the first phase.
Steps of the Algorithm (Phase I)
1. Express the given LPP in the standard form.
2. Convert each of the constraints into equality by introducing slack, surplus or artificial
variables.
3. Solve the LPP by assigning a coefficient of ‘-1’ to each artificial variable in case of
maximisation problem and ‘+1’ in case of minimisation problem and zero to all other
variables in the objective function.
4. Apply the simplex algorithm to solve this LPP.
5. If Cj–Zj row indicates optimal solution and
a. the artificial variable appears as a basic variable, the given LPP has non-feasible
solution.
b. the artificial variable does not appear as a basic variable, the given LPP has a feasible
solution and we proceed to Phase II.
Phase II
6. Assign actual coefficients to the variables in the objective function and zero to the
artificial variables. That is, the last simplex table of phase I is used as the initial simplex
table for phase II. Now apply the usual simplex algorithm to the modified simplex table
to get the optimal solution to the original problem.
𝑀𝑖𝑛. 𝑧 = 𝑥1 + 𝑥2
𝑠/𝑡
2𝑥1 + 𝑥2 ≥ 4
𝑥1 + 7𝑥2 ≥ 7
𝑥1, 𝑥2 ≥ 0
𝐼𝑛𝑡𝑟𝑜𝑑𝑢𝑐𝑖𝑛𝑔 𝑠𝑢𝑟𝑝𝑙𝑢𝑠 𝑎𝑛𝑑 𝑎𝑟𝑡𝑖𝑓𝑖𝑐𝑖𝑎𝑙 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 (𝑃ℎ𝑎𝑠𝑒 𝐼 𝑜𝑓 𝑡ℎ𝑒 𝑡𝑤𝑜 − 𝑝ℎ𝑎𝑠𝑒
𝑚𝑒𝑡ℎ𝑜𝑑)
𝑀𝑖𝑛. 𝑧 = 0𝑥1 + 0𝑥2 + 0𝑆1 + 0𝑆2 + 𝐴1 + 𝐴2
𝑠/𝑡
2𝑥1 + 𝑥2 − 𝑆1 + 𝐴1 = 4
𝑥1 + 7𝑥2 − 𝑆2 + 𝐴2 = 7
𝑥1, 𝑥2, 𝑆1, 𝑆2, 𝐴1, 𝐴2 ≥ 0
𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 = 6
𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛𝑠 = 2
∴ 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑛𝑜𝑛 − 𝑏𝑎𝑠𝑖𝑐 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 = 6 − 2 = 4
∴ 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑎𝑠𝑖𝑐 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 = 6 − 4 = 2
𝑇ℎ𝑒 𝑡𝑤𝑜 𝑎𝑟𝑡𝑖𝑓𝑖𝑐𝑖𝑎𝑙 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 𝐴1 𝑎𝑛𝑑 𝐴2 𝑤𝑖𝑙𝑙 𝑏𝑒 𝑡𝑎𝑘𝑒𝑛 𝑎𝑠 𝑖𝑛𝑖𝑡𝑖𝑎𝑙 𝑏𝑎𝑠𝑖𝑐 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠
𝐴1 = 4
𝐴2 = 7

6. Initial Simplex Table (Phase I)
Cj 0 0 0 0 1 1
Cb BV SV x1 x2 S1 S2 A1 A2
1 A1 4 2 1 -1 0 1 0
4
1
= 4
1 A2 7 1 7 0 -1 0 1
7
7
= 1 
Zj 11 3 8 -1 -1 1 1
Cj–Zj -3 -8 1 1 0 0

Intermediate Simplex Table (Phase I)
1 A1 3
13
7
0 -1
1
7
1 ×
3
13
7
=
21
13 𝑅1 = 𝑅1 − 𝑅2 
0 x2 1
1
7
1 0 −
1
7
0 ×
1
1
7
= 7 𝑅2 =
𝑅2
7
Zj 3
13
7
0 -1
1
7
1 ×
Cj–Zj −
13
7
0 1 −
1
7
0 ×

∵ 𝐴2 ℎ𝑎𝑠 𝑙𝑒𝑓𝑡 𝑡ℎ𝑒 𝑏𝑎𝑠𝑖𝑠
∴ 𝑤𝑒 𝑛𝑒𝑒𝑑 𝑛𝑜𝑡 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒 𝑡ℎ𝑒 𝑣𝑎𝑙𝑢𝑒𝑠 𝑖𝑛 𝑖𝑡𝑠 𝑐𝑜𝑙𝑢𝑚𝑛
Final Simplex Table (Phase I)
0 x1
21
13
1 0 −
7
13
1
13
× × 𝑅1 =
7
13
𝑅1
0 x2
10
13
0 1
1
13
−
2
13
× × 𝑅2 = 𝑅2 −
1
7
𝑅1
Zj 0 0 0 0 0 × ×
Cj–Zj 0 0 0 0 × ×
∵ 𝑎𝑙𝑙 𝐶𝑗 − 𝑍𝑗 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑠 𝑎𝑟𝑒 𝑧𝑒𝑟𝑜 𝑎𝑛𝑑 𝑎𝑙𝑙 𝑎𝑟𝑡𝑖𝑓𝑖𝑐𝑖𝑎𝑙 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 ℎ𝑎𝑣𝑒 𝑙𝑒𝑓𝑡 𝑡ℎ𝑒 𝑏𝑎𝑠𝑖𝑠
∴ 𝑤𝑒 𝑠ℎ𝑎𝑙𝑙 𝑒𝑛𝑡𝑒𝑟 𝑃ℎ𝑎𝑠𝑒 𝐼𝐼
Phase II Simplex Table (Optimum)
Cj 1 1 0 0
Cb BV SV x1 x2 S1 S2
1 x1
21
13
1 0 −
7
13
1
13
1 x2
10
13
0 1
1
13
−
2
13
Zj
31
13
1 1 −
6
13
−
1
13
Cj–Zj 0 0
6
13
1
13
𝑨𝒏𝒔: 𝒙 𝟏 =
𝟐𝟏
𝟏𝟑
, 𝒙 𝟐 =
𝟏𝟎
𝟏𝟑
, 𝒛 =
𝟑𝟏
𝟏𝟑

7. Solve the following using two-phase method:
Maximise: z = 30x + 40y + 35z
Subject to the constraints:
3x + 4y +2z ≤ 90
2x + y +2z ≤ 54
X + 3y + 2z ≤ 93
x, y, z ≥ 0 (2013)