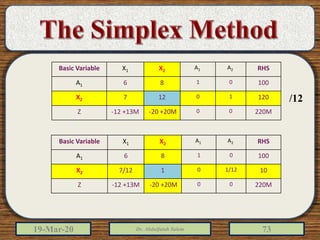
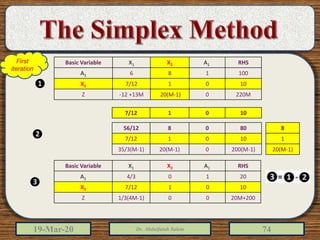
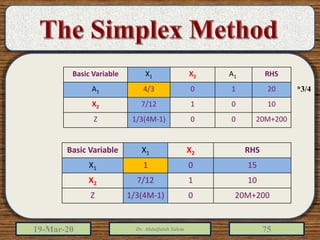
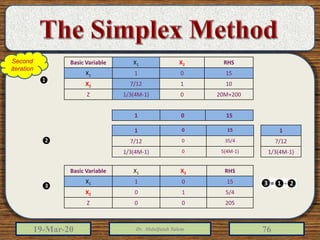
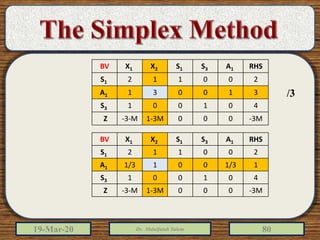
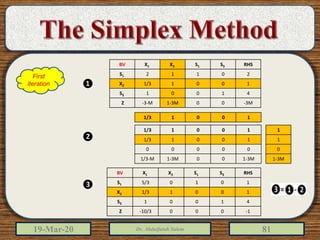
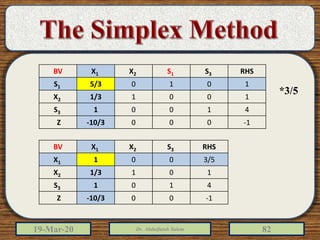
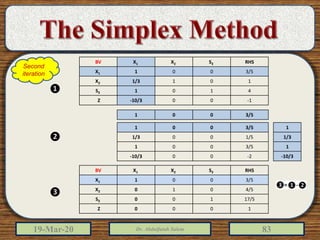
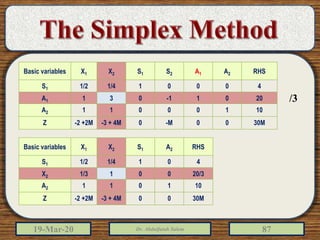
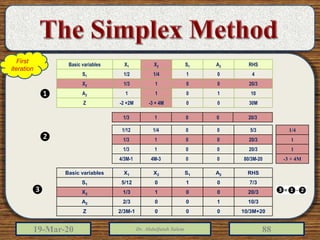
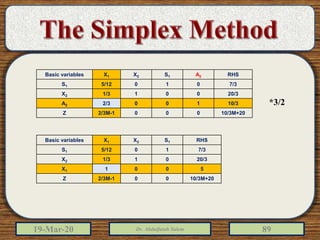
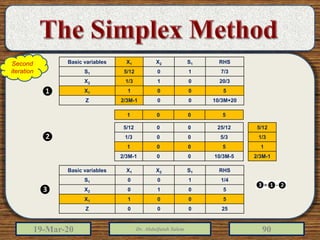
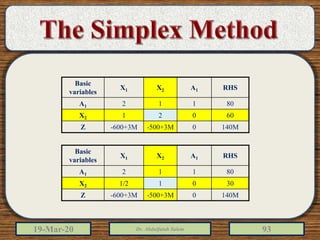
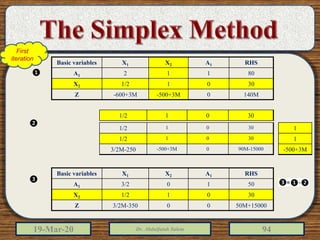
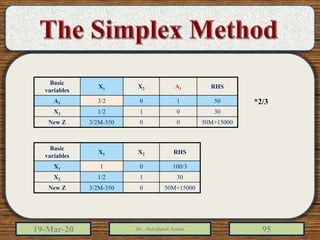
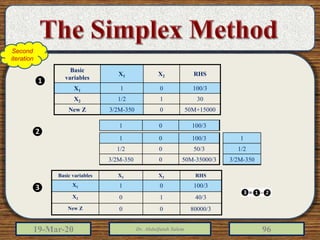
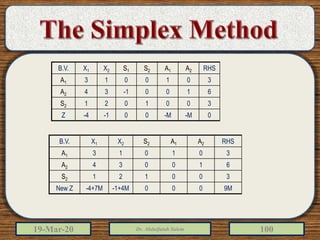
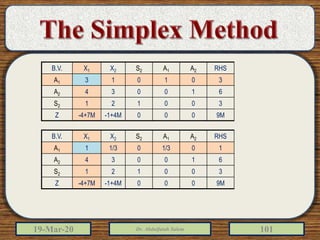
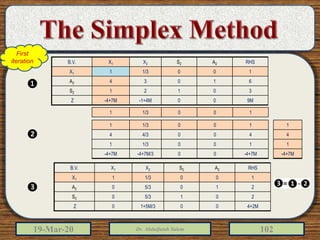
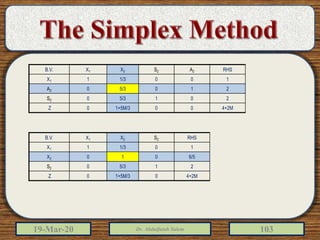
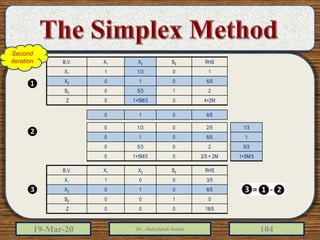
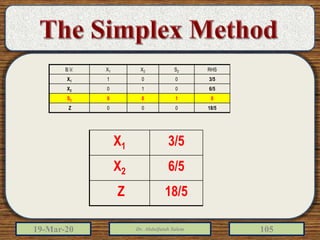
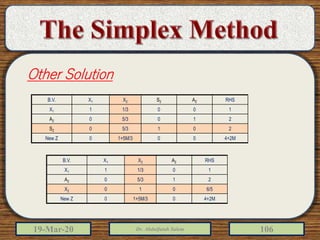
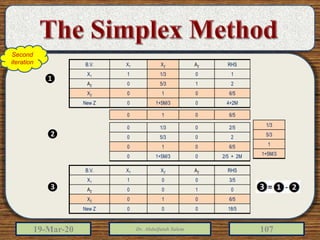
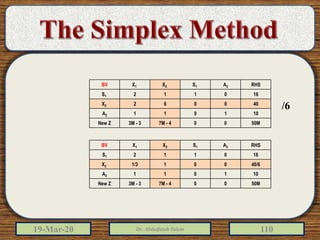
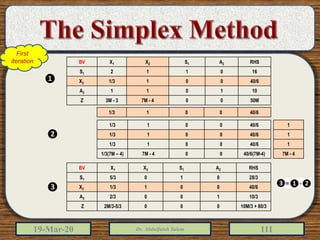
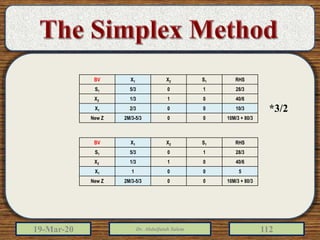
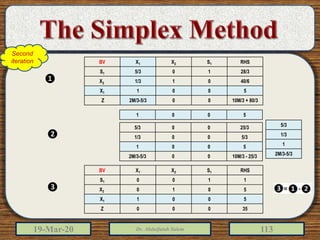
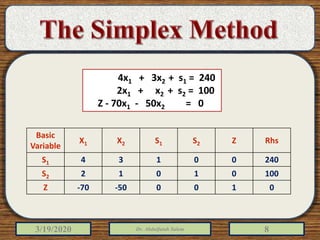
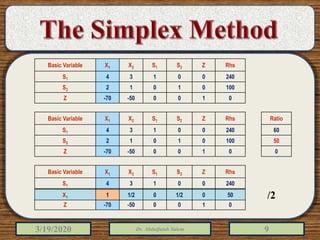
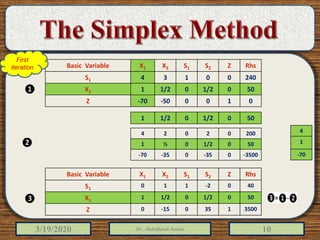
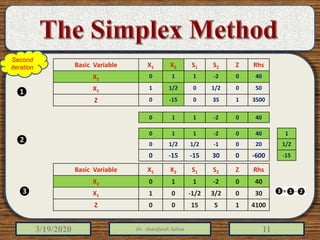
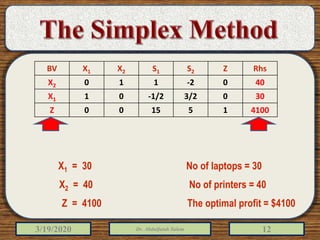
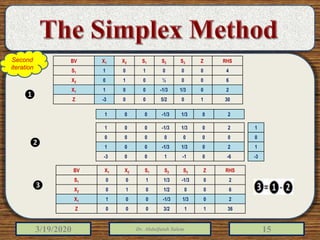
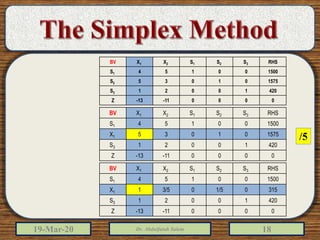
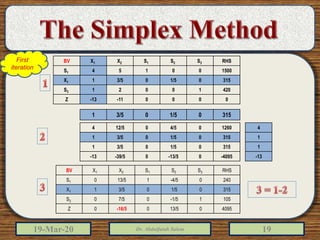
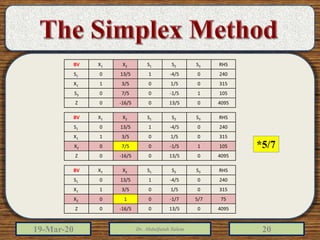
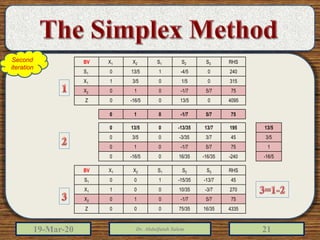
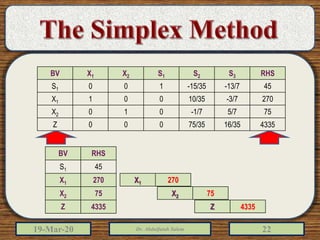
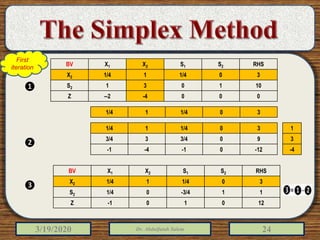
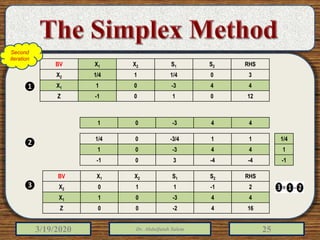
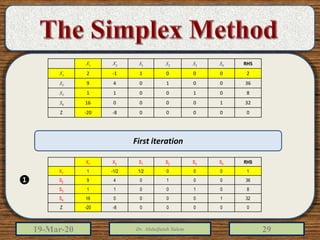
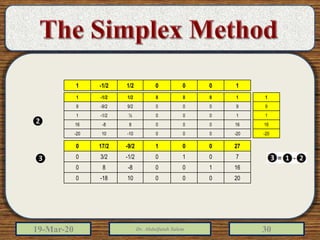
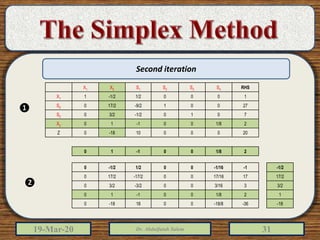
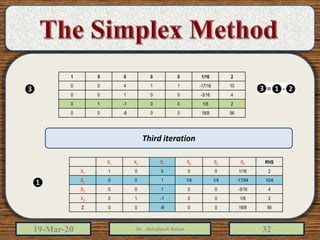
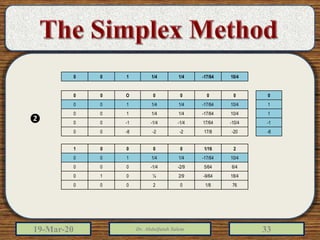
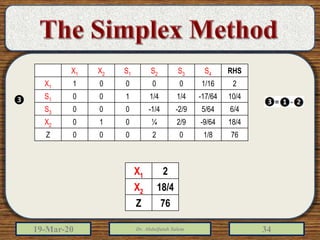
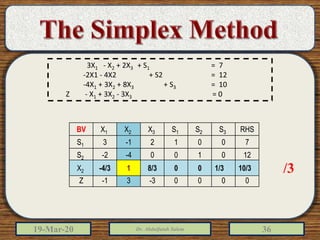
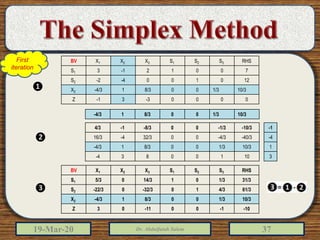
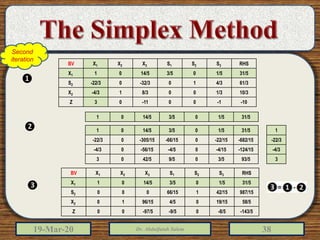
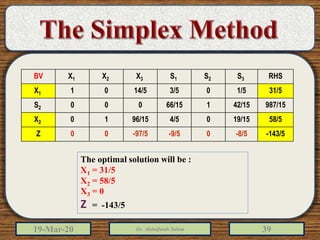
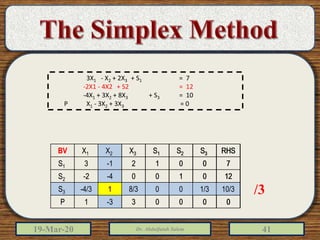
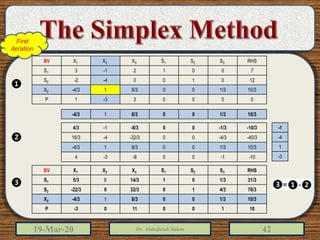
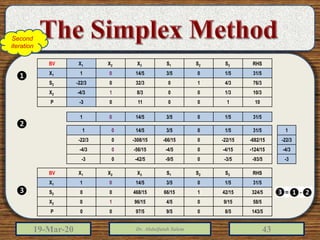
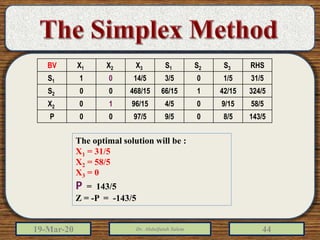
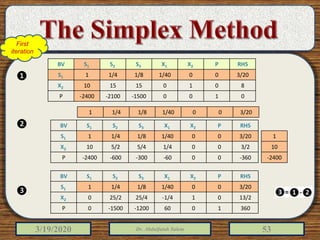
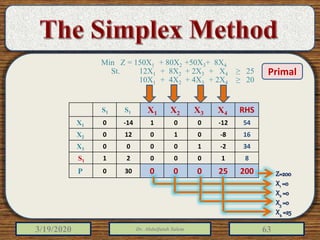
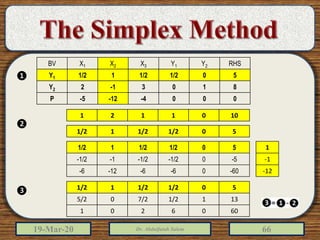
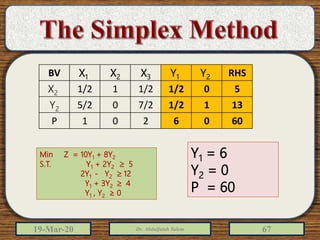
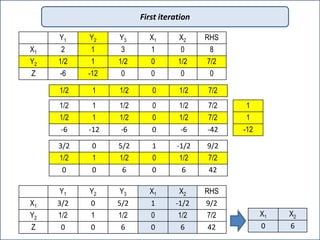
The document discusses the simplex method for solving linear programming problems. It explains that the simplex method is an iterative procedure developed by George Dantzig in 1946 to systematically examine the vertices of the feasible region to determine the optimal value of the objective function. The document then provides steps for applying the simplex method, including preparing the problem in standard form, creating an initial simplex tableau, selecting pivot columns and rows, and using row operations to solve for an optimal solution. An example problem is presented and solved using the simplex method in 3 iterations to find the optimal values.
































![19-Mar-20 Dr. Abdulfatah Salem 69
Solving the non standard LP model
The Method
Suppose that you add n artificial variables A1 , A2 , …. , An to the LP model
Build the initial tableau representing the LP model with rows representing the
constraints’ equations and last row representing the modified objective function
Ž where :
Model modification
Add M[A1 + A2 + …. + An]to the objective function Eqn. if the model is Min.
Subtract M[A1 + A2 + …. + An] from the objective function Eqn. if the model is Max.
Ž row = Z row + M[A1row + A2row + …. + Anrow] if the model is Min.
Ž row = Z row - M[A1row + A2row + …. + Anrow] if the model is Max.](https://image.slidesharecdn.com/linearprogramming-simplexmethod-200319210511/85/Linear-programming-simplex-method-69-320.jpg)