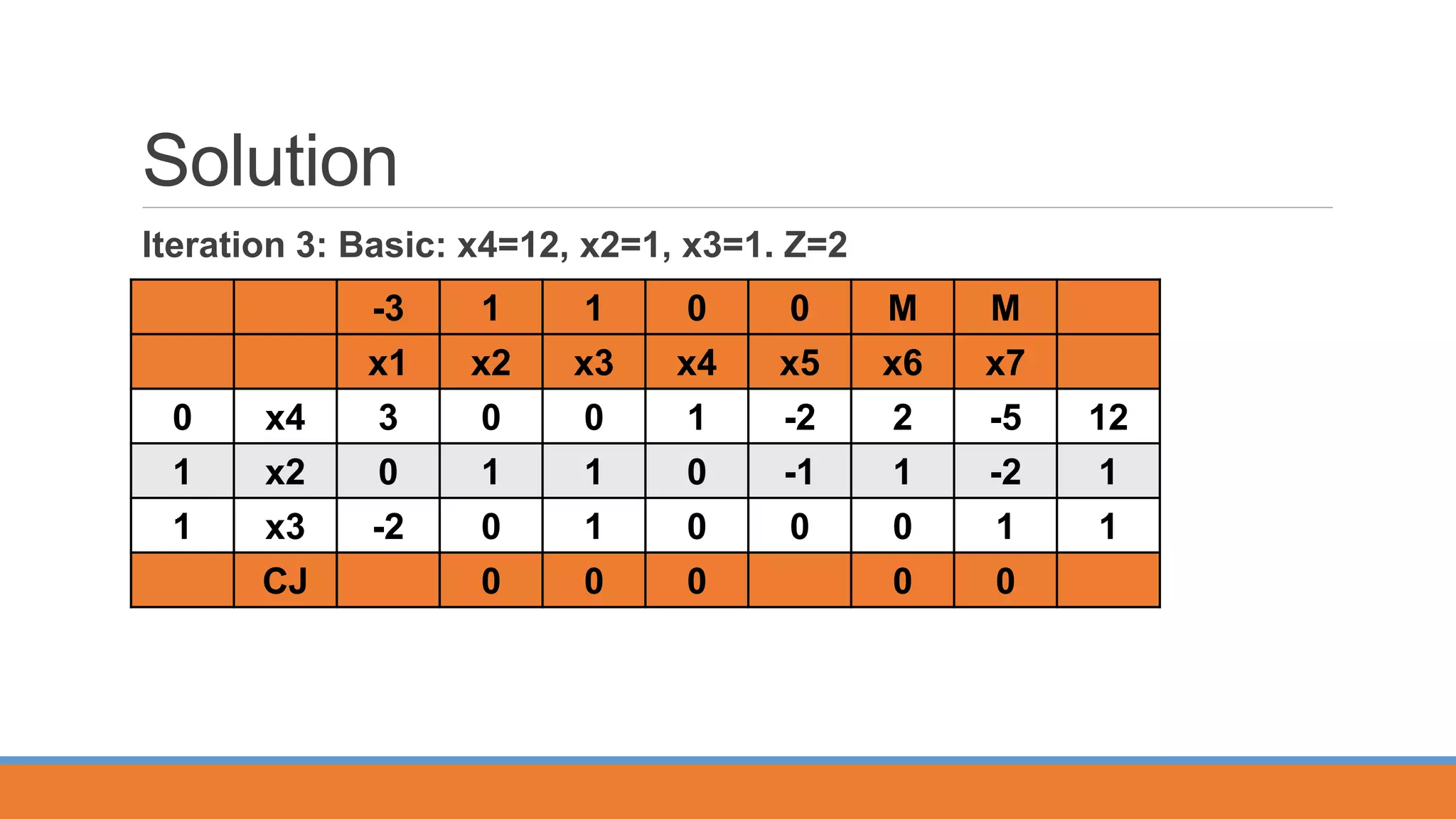
The Big M Method is used to solve linear programming problems with inequality constraints. It involves (1) multiplying inequality constraints to make the right hand side positive, (2) introducing surplus and artificial variables for greater-than constraints, (3) adding a large penalty M to the objective for artificial variables, and (4) introducing slack variables to convert all constraints to equalities. The method is demonstrated on a sample minimization problem that is converted to standard form and solved using the simplex method.

1. Operation Research
CHAPTER 06 - THE BIG M METHOD

2. The Big M Method
I. Multiply the inequality constraints to ensure that the right hand
side is positive.
II. For any greater-than or equal constraints, introduce surplus and
artificial variables.
III. Choose a large positive M and introduce a term in the objective of
the form M multiplying the artificial variables.
IV. For less-than constraints, introduce slack variables so that all
constraints are equalities.
V. Solve the problem using the usual simplex method.

3. Example
Min Z= -3x1 + x2 + x3
S.T. x1 – 2x2 + x3 <= 11
-4x1+ x2 + 2x3 >= 3
2x1 – x3 = -1

4. Solution
Write the problem in standard form and let the right hand side
positive.
Min Z= -3x1 + x2 + x3
S.T. x1 – 2x2 + x3 + x4 = 11, Slack
-4x1 + x2 +2x3 – x5 = 3, Surplus
-2x1 + x3 = 1

5. Solution
Write the problem in canonical form (add artificial variable to the 2nd
and to the 3rd constraints).
Add M to the artificial variables in the objective function
In case the problem is a maximization problem, add –M as a
coefficient to the artificial variables, Otherwise add M.
Min Z= -3x1 + x2 + x3 + Mx6 + Mx7
S.T. x1 – 2x2 + x3 + x4 = 11
-4x1 + x2 +2x3 – x5 + x6 = 3
-2x1 + x3 + x7 = 1

6. Solution
Iteration 1: Basic: x4=11, x6=3, x7=1. Z=Mx6+Mx7=3M+M=4M
-3 1 1 0 0 M M
x1 x2 x3 x4 x5 x6 x7
0 x4 1 -2 1 1 0 0 0 11
M x6 -4 1 2 0 -1 1 0 3
M x7 -2 0 1 0 0 0 1 1
CJ 0 0 0

7. Solution
C1= -3 – (0,M,M) = 6M-3 >0
C2= 1 – (0,M,M) = 1-M <0
C3= 1 – (0,M,M) = 1-3M <0
C5= 0 – (0,M,M) = M >0
x3 is entering, x3= min{11,3/2,1}=1, x7 is leaving.
1
-4
-2
-2
1
0
1
2
1
0
-1
0

8. Solution
Iteration 2: Basic: x4=11-1=10, x6=3-2=1, x3=1. Z=1+M
-3 1 1 0 0 M M
x1 x2 x3 x4 x5 x6 x7
0 x4 3 -2 0 1 0 0 -1 10
M x6 0 1 0 0 -1 1 -2 1
1 x3 -2 0 1 0 0 0 1 1
CJ 0 0 0 0

9. Solution
C1= -3 – (0,M,1) = -1 <0
C2= 1 – (0,M,1) = 1-M <0
C5= 0 – (0,M,1) = M >0
x2 is entering, x2= min{-5,1,inf.}=1, x6 is leaving.
Basic: x4=12, x2=1, x3=1. Z=2.
3
0
-2
-2
1
0
0
-1
0

10. Solution
Iteration 3: Basic: x4=12, x2=1, x3=1. Z=2
-3 1 1 0 0 M M
x1 x2 x3 x4 x5 x6 x7
0 x4 3 0 0 1 -2 2 -5 12
1 x2 0 1 1 0 -1 1 -2 1
1 x3 -2 0 1 0 0 0 1 1
CJ 0 0 0 0 0

11. Solution
C1= -3 – (0,1,1) = -1 <0
C5= 0 – (0,1,1) = 1 >0
x1 is entering, x1= min{4,inf.,-1/2}=4, x4 is leaving.
Basic: x1=4, x2=1, x3=9. Z=-2.
3
0
-2
-2
-1
0

12. Solution
Iteration 4: Basic: x1=4, x2=1, x3=9. Z=-2
-3 1 1 0 0 M M
x1 x2 x3 x4 x5 x6 x7
-3 x1 1 0 0 1/3 -2/3 2/3 -5/3 4
1 x2 0 1 0 0 -1 1 -2 1
1 x3 0 0 1 2/3 -4/3 4/3 -7/3 9
CJ 0 0 0 0 0 0

13. Solution
C5= 0 – (-3,1,1) = 1/3 >0
No entering variables.
The current solution is optimal.
x1=4, x2=1, x3=9, Z=-2
-2/3
-1
-4/3