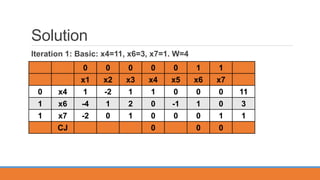
The two phase simplex method is used to solve linear programming problems. Phase I creates an artificial objective function to find a basic feasible solution. If the minimum is zero, a basic feasible solution exists and phase II begins. Phase II uses the original objective function and tableau from phase I to find an optimal solution. The example problem is solved using this two phase method, with phase I minimizing artificial variables to find a basic feasible solution, then phase II optimizing the original objective function.

1. Operations Research
CHAPTER 07 - THE TWO PHASE SIMPLEX METHOD

2. The Two Phase Simplex Method
Phase I: We create an artificial objective function as the sum of all
the artificial variables, and we minimize this objective function using
the tableau simplex method.
If the minimum value of this artificial objective function is zero, then
this means that all the artificial variables have been reduced to zero,
and we have a basic feasible solution to the original problem, and
we proceed to phase II. If this minimum value is positive, then this
means that the original problem is infeasible, so we terminate.
Phase II: The final tableau of phase I becomes the first tableau of
phase II using the original objective function now. Use the tableau
method again to obtain an optimal solution.

3. Example
Min Z= -3x1 + x2 + x3
S.T. x1 – 2x2 + x3 <= 11
-4x1 + x2 +2x3 >= 3
-2x1 + x3 = 1

4. Solution
Write the problem in standard form
Min Z= -3x1 + x2 + x3
S.T. x1 – 2x2 + x3 + x4 = 11
-4x1 + x2 +2x3 - x5 = 3
-2x1 + x3 = 1

5. Solution
Write the problem in canonical form (add artificial variable to the 2nd
and to the 3rd constraints)
Min Z= -3x1 + x2 + x3
S.T. x1 – 2x2 + x3 + x4 = 11
-4x1 + x2 +2x3 - x5 + x6 = 3
-2x1 + x3 + x7 = 1

6. Solution
Phase 1: -Change Z to W and add to it the artificial variables
-W is always minimized
-Keep the constraints
Min W= x6 + x7
S.T. x1 – 2x2 + x3 + x4 = 11
-4x1 + x2 +2x3 - x5 + x6 = 3
-2x1 + x3 + x7 = 1

7. Solution
Iteration 1: Basic: x4=11, x6=3, x7=1. W=4
0 0 0 0 0 1 1
x1 x2 x3 x4 x5 x6 x7
0 x4 1 -2 1 1 0 0 0 11
1 x6 -4 1 2 0 -1 1 0 3
1 x7 -2 0 1 0 0 0 1 1
CJ 0 0 0

8. Solution
C1= 0 – (0,1,1) = 6
C2= 0 – (0,1,1) = -1
C3= 0 – (0,1,1) = -3
C5= 0 – (0,1,1) = 1
x3 is entering, x3= min{11,3/2,1}=1, x7 is leaving.
1
-4
-2
-2
1
0
1
2
1
0
-1
0

9. Solution
Iteration 2: Basic: x4=11-1=10, x6=3-2=1, x3=1. W=1
0 0 0 0 0 1 1
x1 x2 x3 x4 x5 x6 x7
0 x4 3 -2 0 1 0 0 -1 10
1 x6 0 1 0 0 -1 1 -2 1
0 x3 -2 0 1 0 0 0 1 1
CJ 0 0 0 0

10. Solution
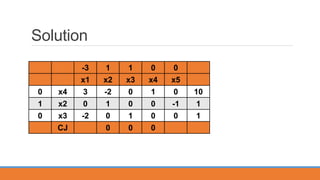
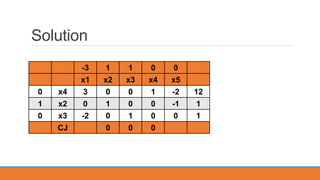
C1= 0 – (0,1,1) = 0
C2= 0 – (0,1,1) = -1
C5= 0 – (0,1,1) = 1
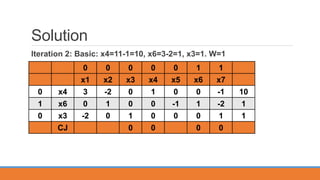
x2 is entering, x2= min{-5,1,inf.}=1, x6 is leaving.
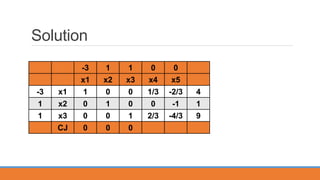
Basic: x4=12, x2=1, x3=1. W=0 [End of phase 1 because W is zero].
3
0
-2
-2
1
0
0
-1
0

11. Solution
Phase 2: -Change W to Z and remove the artificial variables
-The same last table but remove the artificial variables
columns

12. Solution
-3 1 1 0 0
x1 x2 x3 x4 x5
0 x4 3 -2 0 1 0 10
1 x2 0 1 0 0 -1 1
0 x3 -2 0 1 0 0 1
CJ 0 0 0

13. Solution
-3 1 1 0 0
x1 x2 x3 x4 x5
0 x4 3 0 0 1 -2 12
1 x2 0 1 0 0 -1 1
0 x3 -2 0 1 0 0 1
CJ 0 0 0

14. Solution
C1= -3 – (0,1,1) = -1
C5= 0 – (0,1,1) = 1
x1 is entering, x1= min{4,inf.,-1/2}=4, x4 is leaving.
Basic: x1=4, x2=1, x3=9. Z=-12+1+9=-2.
3
0
-2
-2
-1
0

15. Solution
-3 1 1 0 0
x1 x2 x3 x4 x5
-3 x1 1 0 0 1/3 -2/3 4
1 x2 0 1 0 0 -1 1
1 x3 0 0 1 2/3 -4/3 9
CJ 0 0 0

16. Solution
C4= 0 – (-3,1,1) = 1/3 > 0
C5= 0 – (-3,1,1) = 1/3 > 0
No entering variables, and the current solution is optimal.
Basic: x1=4, x2=1, x3=9. Z=-12+1+9=-2.
1/3
0
2/3
-2/3
-1
-4/3