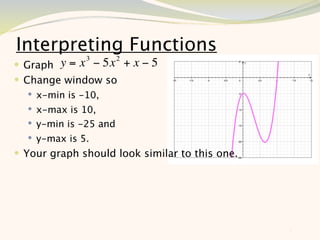
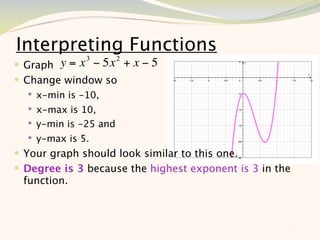
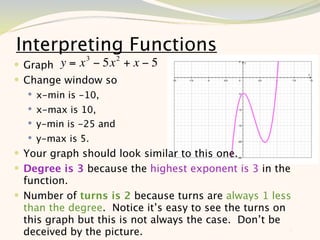
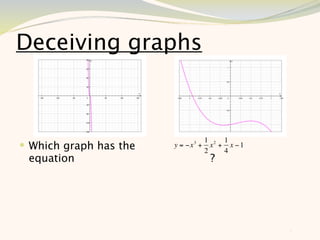
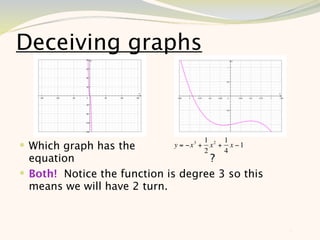
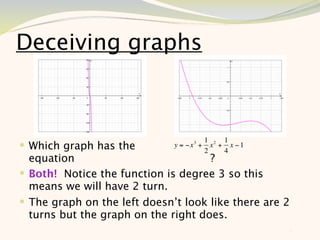
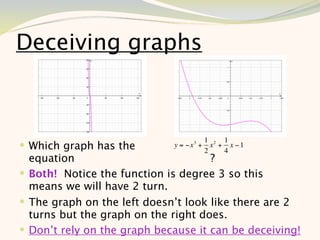
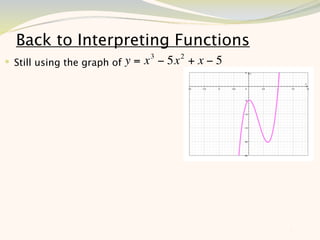
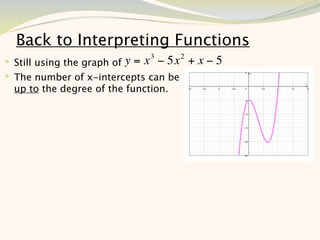
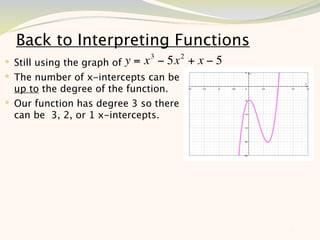
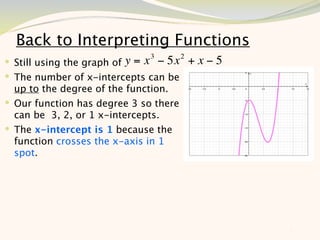
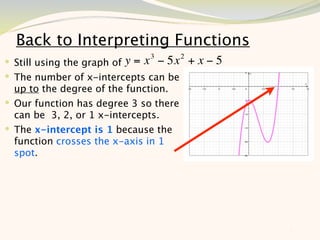
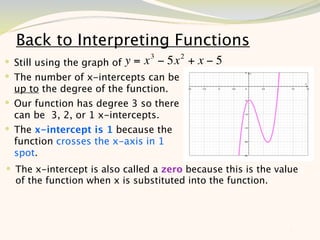
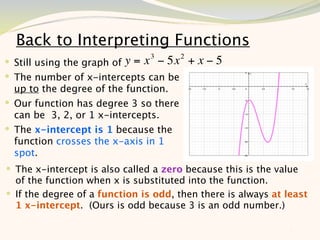
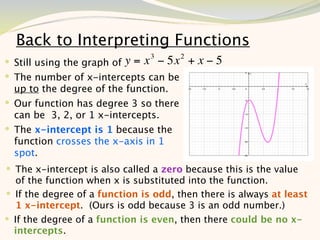
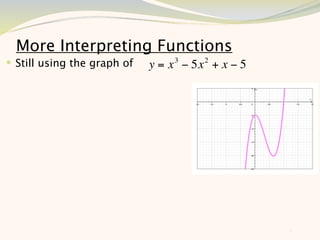
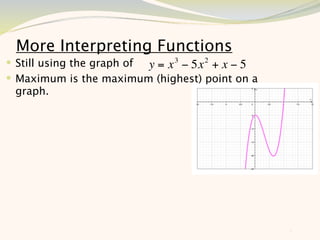
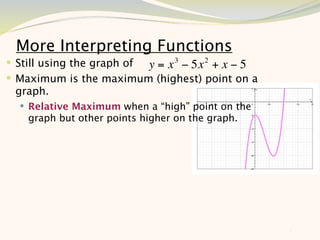
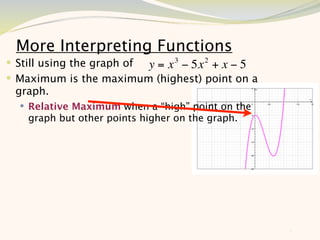
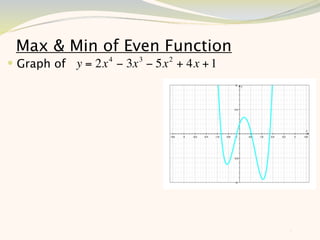
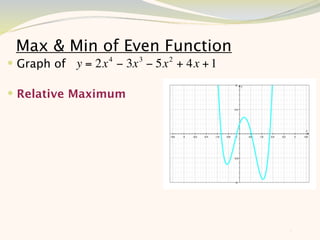
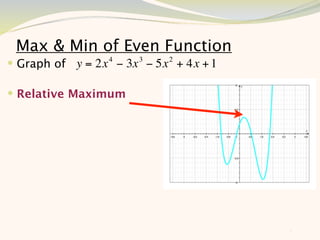
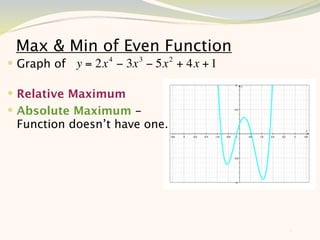
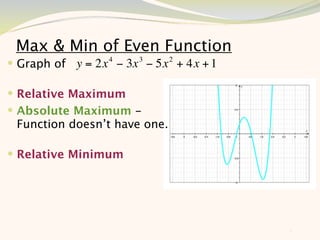
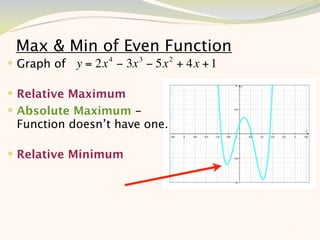
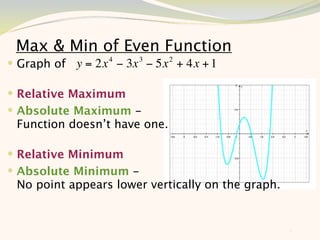
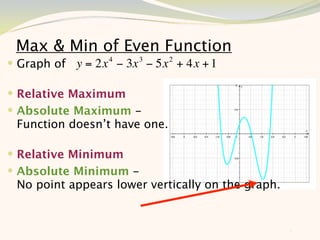
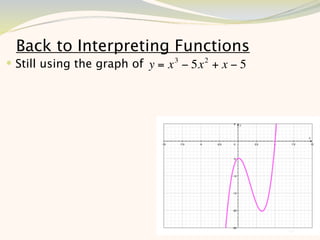
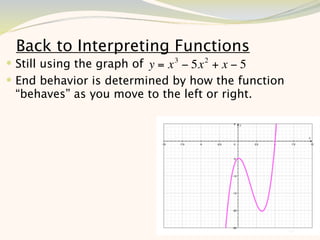
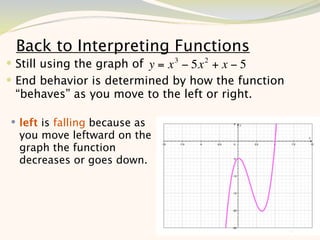
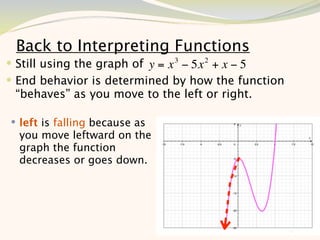
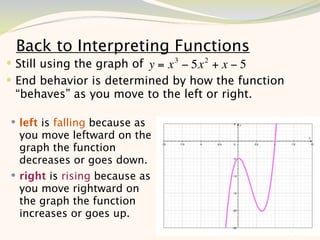
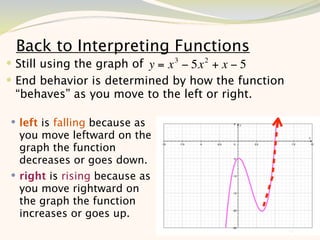
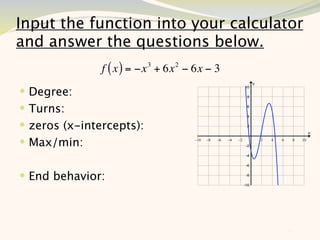
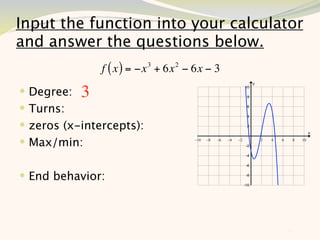
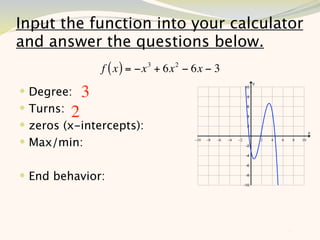
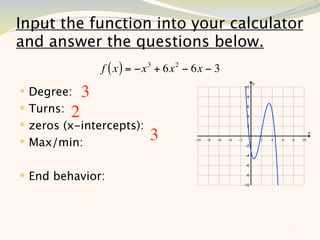
The document discusses graphing and interpreting various polynomial functions using a graphing calculator. It examines the graphs of y=x-1, y=x^2-4, and y=x^3+x^2-12 to note their similarities and differences in terms of degree, number of turns, and x-intercepts. It then explores how changing the coefficients of a cubic function impacts its graph. Finally, it interprets key features of the graph of y=x^3-5x^2+x-5 such as its degree, number of turns, x-intercept, maximum and minimum points.

2. Polynomial Functions
Using a graphing calculator , graph each equation
below separately.

3. Polynomial Functions
Using a graphing calculator , graph each equation
below separately.
1. Note and Similarities and Differences

4. Polynomial Functions
Using a graphing calculator , graph each equation
below separately.
1. Note and Similarities and Differences
2. Compare the number of x-intercepts, number
of turns, and the degree of the polynomial.
Y=x-1
 Y = x2 - 4
 Y = x3 + x2 - 12

5. Polynomial Functions

6. Polynomial Functions
Y = x – 1
The graph is a line with degree 1, 0 turns,
and 1 x-intercept.

7. Polynomial Functions
Y = x – 1
The graph is a line with degree 1, 0 turns,
and 1 x-intercept.
 Y = x2 – 4
The graph is a parabola with degree 2, 1
turn, and 2 x-intercepts.

8. Polynomial Functions
Y = x – 1
The graph is a line with degree 1, 0 turns,
and 1 x-intercept.
 Y = x2 – 4
The graph is a parabola with degree 2, 1
turn, and 2 x-intercepts.
 Y = x3 + x2 - 12
The graph is curvy with degree 3, 2 turns,
and 3 x-intercepts.

9. Exploring Graphs of
Polynomial Functions
Use the link below to explore an interactive Gizmo
to see how the graph changes as you change the
coefficients
of the cubic (degree 3) function.
EXPLORING GRAPHS OF POLYNOMIALS

10. Interpreting Functions
 Graph y = x 3 − 5x 2 + x − 5
5

11. Interpreting Functions
 Graph y = x 3 − 5x 2 + x − 5
 Change window so
 x-min is -10,
 x-max is 10,
 y-min is -25 and
 y-max is 5.
5

12. Interpreting Functions
 Graph y = x 3 − 5x 2 + x − 5
 Change window so
 x-min is -10,
 x-max is 10,
 y-min is -25 and
 y-max is 5.
 Your graph should look similar to this one.
5

13. Interpreting Functions
 Graph y = x 3 − 5x 2 + x − 5
 Change window so
 x-min is -10,
 x-max is 10,
 y-min is -25 and
 y-max is 5.
 Your graph should look similar to this one.
 Degree is 3 because the highest exponent is 3 in the
function.
5

14. Interpreting Functions
 Graph y = x 3 − 5x 2 + x − 5
 Change window so
 x-min is -10,
 x-max is 10,
 y-min is -25 and
 y-max is 5.
 Your graph should look similar to this one.
 Degree is 3 because the highest exponent is 3 in the
function.
 Number of turns is 2 because turns are always 1 less
than the degree. Notice it’s easy to see the turns on
this graph but this is not always the case. Don’t be
deceived by the picture. 5

15. Deceiving graphs
1 2 1
 Which graph has the y = −x 3 +
2
x + x −1
4
equation ?
6

16. Deceiving graphs
1 2 1
 Which graph has the y = −x 3 +
2
x + x −1
4
equation ?
 Both! Notice the function is degree 3 so this
means we will have 2 turn.
6

17. Deceiving graphs
1 2 1
 Which graph has the y = −x 3 +
2
x + x −1
4
equation ?
 Both! Notice the function is degree 3 so this
means we will have 2 turn.
 The graph on the left doesn’t look like there are 2
turns but the graph on the right does.
6

18. Deceiving graphs
1 2 1
 Which graph has the y = −x 3 +
2
x + x −1
4
equation ?
 Both! Notice the function is degree 3 so this
means we will have 2 turn.
 The graph on the left doesn’t look like there are 2
turns but the graph on the right does.
 Don’t rely on the graph because it can be deceiving!
6

19. Back to Interpreting Functions
3 2
 Still using the graph of y = x − 5x + x − 5
7

20. Back to Interpreting Functions
3 2
 Still using the graph of y = x − 5x +x−5
 The number of x-intercepts can be
up to the degree of the function.
7

21. Back to Interpreting Functions
3 2
 Still using the graph of y = x − 5x +x−5
 The number of x-intercepts can be
up to the degree of the function.
 Our function has degree 3 so there
can be 3, 2, or 1 x-intercepts.
7

22. Back to Interpreting Functions
3 2
 Still using the graph of y = x − 5x +x−5
 The number of x-intercepts can be
up to the degree of the function.
 Our function has degree 3 so there
can be 3, 2, or 1 x-intercepts.
 The x-intercept is 1 because the
function crosses the x-axis in 1
spot.
7

23. Back to Interpreting Functions
3 2
 Still using the graph of y = x − 5x +x−5
 The number of x-intercepts can be
up to the degree of the function.
 Our function has degree 3 so there
can be 3, 2, or 1 x-intercepts.
 The x-intercept is 1 because the
function crosses the x-axis in 1
spot.
7

24. Back to Interpreting Functions
3 2
 Still using the graph of y = x − 5x +x−5
 The number of x-intercepts can be
up to the degree of the function.
 Our function has degree 3 so there
can be 3, 2, or 1 x-intercepts.
 The x-intercept is 1 because the
function crosses the x-axis in 1
spot.
 The x-intercept is also called a zero because this is the value
of the function when x is substituted into the function.
7

25. Back to Interpreting Functions
3 2
 Still using the graph of y = x − 5x +x−5
 The number of x-intercepts can be
up to the degree of the function.
 Our function has degree 3 so there
can be 3, 2, or 1 x-intercepts.
 The x-intercept is 1 because the
function crosses the x-axis in 1
spot.
 The x-intercept is also called a zero because this is the value
of the function when x is substituted into the function.
 If the degree of a function is odd, then there is always at least
1 x-intercept. (Ours is odd because 3 is an odd number.)
7

26. Back to Interpreting Functions
3 2
 Still using the graph of y = x − 5x +x−5
 The number of x-intercepts can be
up to the degree of the function.
 Our function has degree 3 so there
can be 3, 2, or 1 x-intercepts.
 The x-intercept is 1 because the
function crosses the x-axis in 1
spot.
 The x-intercept is also called a zero because this is the value
of the function when x is substituted into the function.
 If the degree of a function is odd, then there is always at least
1 x-intercept. (Ours is odd because 3 is an odd number.)
 If the degree of a function is even, then there could be no x-
intercepts. 7

27. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
8

28. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 Maximum is the maximum (highest) point on a
graph.
8

29. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 Maximum is the maximum (highest) point on a
graph.
 Relative Maximum when a “high” point on the
graph but other points higher on the graph.
8

30. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 Maximum is the maximum (highest) point on a
graph.
 Relative Maximum when a “high” point on the
graph but other points higher on the graph.
8

31. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 Maximum is the maximum (highest) point on a
graph.
 Relative Maximum when a “high” point on the
graph but other points higher on the graph.
 Absolute Maximum is when there is no point
higher any where on the graph. Our function
doesn’t have one.
8

32. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 Maximum is the maximum (highest) point on a
graph.
 Relative Maximum when a “high” point on the
graph but other points higher on the graph.
 Absolute Maximum is when there is no point
higher any where on the graph. Our function
doesn’t have one.
 Minimum is a minimum point on a graph.
8

33. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 Maximum is the maximum (highest) point on a
graph.
 Relative Maximum when a “high” point on the
graph but other points higher on the graph.
 Absolute Maximum is when there is no point
higher any where on the graph. Our function
doesn’t have one.
 Minimum is a minimum point on a graph.
 Relative Minimum when a “low” but other points are
lower on the graph.
8

34. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 Maximum is the maximum (highest) point on a
graph.
 Relative Maximum when a “high” point on the
graph but other points higher on the graph.
 Absolute Maximum is when there is no point
higher any where on the graph. Our function
doesn’t have one.
 Minimum is a minimum point on a graph.
 Relative Minimum when a “low” but other points are
lower on the graph.
8

35. More Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 Maximum is the maximum (highest) point on a
graph.
 Relative Maximum when a “high” point on the
graph but other points higher on the graph.
 Absolute Maximum is when there is no point
higher any where on the graph. Our function
doesn’t have one.
 Minimum is a minimum point on a graph.
 Relative Minimum when a “low” but other points are
lower on the graph.
 Absolute Minimum is when not point is lower on
the graph. Our function doesn’t have a minimum.
8

36. Max & Min of Even Function
 Graph of y = 2x 4 − 3x 3 − 5x 2 + 4x + 1
9

37. Max & Min of Even Function
 Graph of y = 2x 4 − 3x 3 − 5x 2 + 4x + 1
 Relative Maximum
9

38. Max & Min of Even Function
 Graph of y = 2x 4 − 3x 3 − 5x 2 + 4x + 1
 Relative Maximum
9

39. Max & Min of Even Function
 Graph of y = 2x 4 − 3x 3 − 5x 2 + 4x + 1
 Relative Maximum
 Absolute Maximum -
Function doesn’t have one.
9

40. Max & Min of Even Function
 Graph of y = 2x 4 − 3x 3 − 5x 2 + 4x + 1
 Relative Maximum
 Absolute Maximum -
Function doesn’t have one.
 Relative Minimum
9

41. Max & Min of Even Function
 Graph of y = 2x 4 − 3x 3 − 5x 2 + 4x + 1
 Relative Maximum
 Absolute Maximum -
Function doesn’t have one.
 Relative Minimum
9

42. Max & Min of Even Function
 Graph of y = 2x 4 − 3x 3 − 5x 2 + 4x + 1
 Relative Maximum
 Absolute Maximum -
Function doesn’t have one.
 Relative Minimum
 Absolute Minimum -
No point appears lower vertically on the graph.
9

43. Max & Min of Even Function
 Graph of y = 2x 4 − 3x 3 − 5x 2 + 4x + 1
 Relative Maximum
 Absolute Maximum -
Function doesn’t have one.
 Relative Minimum
 Absolute Minimum -
No point appears lower vertically on the graph.
9

44. Back to Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
10

45. Back to Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 End behavior is determined by how the function
“behaves” as you move to the left or right.
10

46. Back to Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 End behavior is determined by how the function
“behaves” as you move to the left or right.
 left is falling because as
you move leftward on the
graph the function
decreases or goes down.
10

47. Back to Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 End behavior is determined by how the function
“behaves” as you move to the left or right.
 left is falling because as
you move leftward on the
graph the function
decreases or goes down.
10

48. Back to Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 End behavior is determined by how the function
“behaves” as you move to the left or right.
 left is falling because as
you move leftward on the
graph the function
decreases or goes down.
 right is rising because as
you move rightward on
the graph the function
increases or goes up.
10

49. Back to Interpreting Functions
 Still using the graph of y = x 3 − 5x 2 + x − 5
 End behavior is determined by how the function
“behaves” as you move to the left or right.
 left is falling because as
you move leftward on the
graph the function
decreases or goes down.
 right is rising because as
you move rightward on
the graph the function
increases or goes up.
10

50. Input the function into your calculator
and answer the questions below.
f ( x ) = −x 3 + 6x 2 − 6x − 3
 Degree:
 Turns:
 zeros (x-intercepts):
 Max/min:
 End behavior:
11

51. Input the function into your calculator
and answer the questions below.
f ( x ) = −x 3 + 6x 2 − 6x − 3
 Degree:
 Turns:
 zeros (x-intercepts):
 Max/min:
 End behavior:
11

52. Input the function into your calculator
and answer the questions below.
f ( x ) = −x 3 + 6x 2 − 6x − 3
 Degree: 3
 Turns:
 zeros (x-intercepts):
 Max/min:
 End behavior:
11

53. Input the function into your calculator
and answer the questions below.
f ( x ) = −x 3 + 6x 2 − 6x − 3
 Degree: 3
 Turns: 2
 zeros (x-intercepts):
 Max/min:
 End behavior:
11

54. Input the function into your calculator
and answer the questions below.
f ( x ) = −x 3 + 6x 2 − 6x − 3
 Degree: 3
 Turns: 2
 zeros (x-intercepts):
 Max/min: 3
 End behavior:
11

55. Input the function into your calculator
and answer the questions below.
f ( x ) = −x 3 + 6x 2 − 6x − 3
 Degree: 3
 Turns: 2
 zeros (x-intercepts):
 Max/min: 3
1 relative minimum &
1 relative maximum
 End behavior:
11

56. Input the function into your calculator
and answer the questions below.
f ( x ) = −x 3 + 6x 2 − 6x − 3
 Degree: 3
 Turns: 2
 zeros (x-intercepts):
 Max/min: 3
1 relative minimum &
1 relative maximum
 End behavior:
left rises &
right falls
11

57. Input the function into your calculator
and answer the questions below.
f ( x ) = x 3 − x 2 − 8x + 12
 Degree:
 Turns:
 zeros:
 Max/min:
 End behavior:
12

58. Input the function into your calculator
and answer the questions below.
f ( x ) = x 3 − x 2 − 8x + 12
 Degree: 3
 Turns:
 zeros:
 Max/min:
 End behavior:
12

59. Input the function into your calculator
and answer the questions below.
f ( x ) = x 3 − x 2 − 8x + 12
 Degree: 3
 Turns:2
 zeros:
 Max/min:
 End behavior:
12

60. Input the function into your calculator
and answer the questions below.
f ( x ) = x 3 − x 2 − 8x + 12
 Degree: 3
 Turns: 2
 zeros:
2
 Max/min:
 End behavior:
12

61. Input the function into your calculator
and answer the questions below.
f ( x ) = x 3 − x 2 − 8x + 12
 Degree: 3
 Turns: 2
 zeros:
2
 Max/min:
1 relative maximum &
1 relative minimum
 End behavior:
12

62. Input the function into your calculator
and answer the questions below.
f ( x ) = x 3 − x 2 − 8x + 12
 Degree: 3
 Turns: 2
 zeros:
2
 Max/min:
1 relative maximum &
1 relative minimum
 End behavior:
left falls &
right rises
12

63. Comparing Models

64. Comparing Models
You have looked at best-fit models of linear and
quadratic functions in previous Modules.
Sometimes you can fit data more closely by
using a polynomial model of degree 3 or
greater.

65. Comparing Models
You have looked at best-fit models of linear and
quadratic functions in previous Modules.
Sometimes you can fit data more closely by
using a polynomial model of degree 3 or
greater.
Watch the video below on modeling functions.
VIDEO1

66. Comparing Models
You have looked at best-fit models of linear and
quadratic functions in previous Modules.
Sometimes you can fit data more closely by
using a polynomial model of degree 3 or
greater.
Watch the video below on modeling functions.
VIDEO1
VIDEO 2

67. Comparing Models
You have looked at best-fit models of linear and
quadratic functions in previous Modules.
Sometimes you can fit data more closely by
using a polynomial model of degree 3 or
greater.
Watch the video below on modeling functions.
VIDEO1
VIDEO 2
Now let’s practice finding our own models!

68. Modeling Polynomial
Functions
Sketch a graph and visually determine which
model is a better fit? Linear, Quadratic or
Cubic?
X Y
0 10
5 3
10 8
15 16
20 18

69. Polynomial Functions
Solution: CUBIC MODEL
Find the equation that best models the data in
the table.

70. Polynomial Functions
Solution: CUBIC MODEL
Find the equation that best models the data in
the table.
Reminder:
To enter data: STAT  1:Edit  L1 and L2
To get model: STAT  CALC 
6:CubicReg

71. Polynomial Functions
Solution: CUBIC MODEL
Find the equation that best models the data in
the table.
Reminder:
To enter data: STAT  1:Edit  L1 and L2
To get model: STAT  CALC 
6:CubicReg

72. 3 2
y = −0.012x + 0.42x − 3.2x + 10

73. You finished the notes!
Please complete the
Assignment.