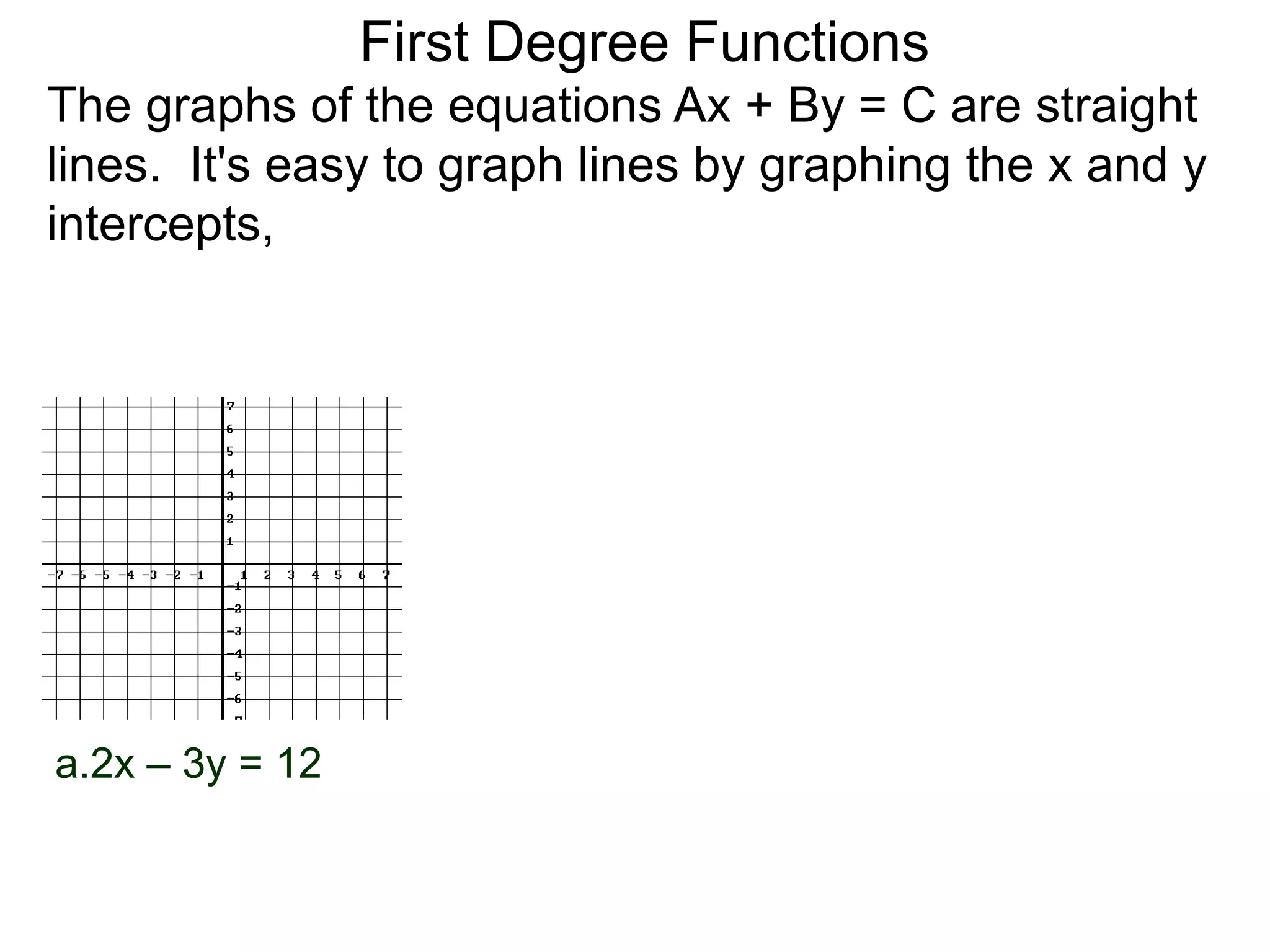
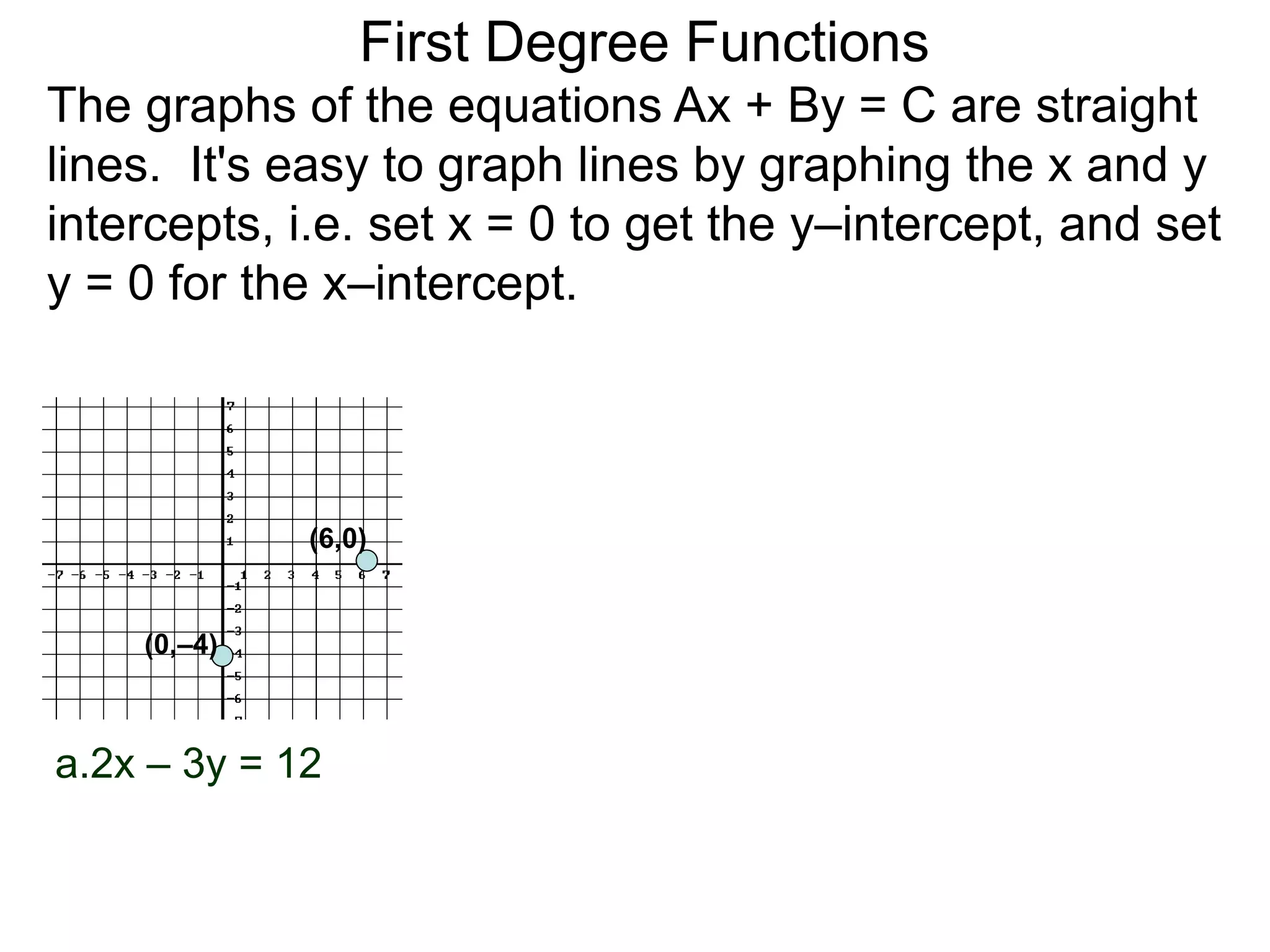
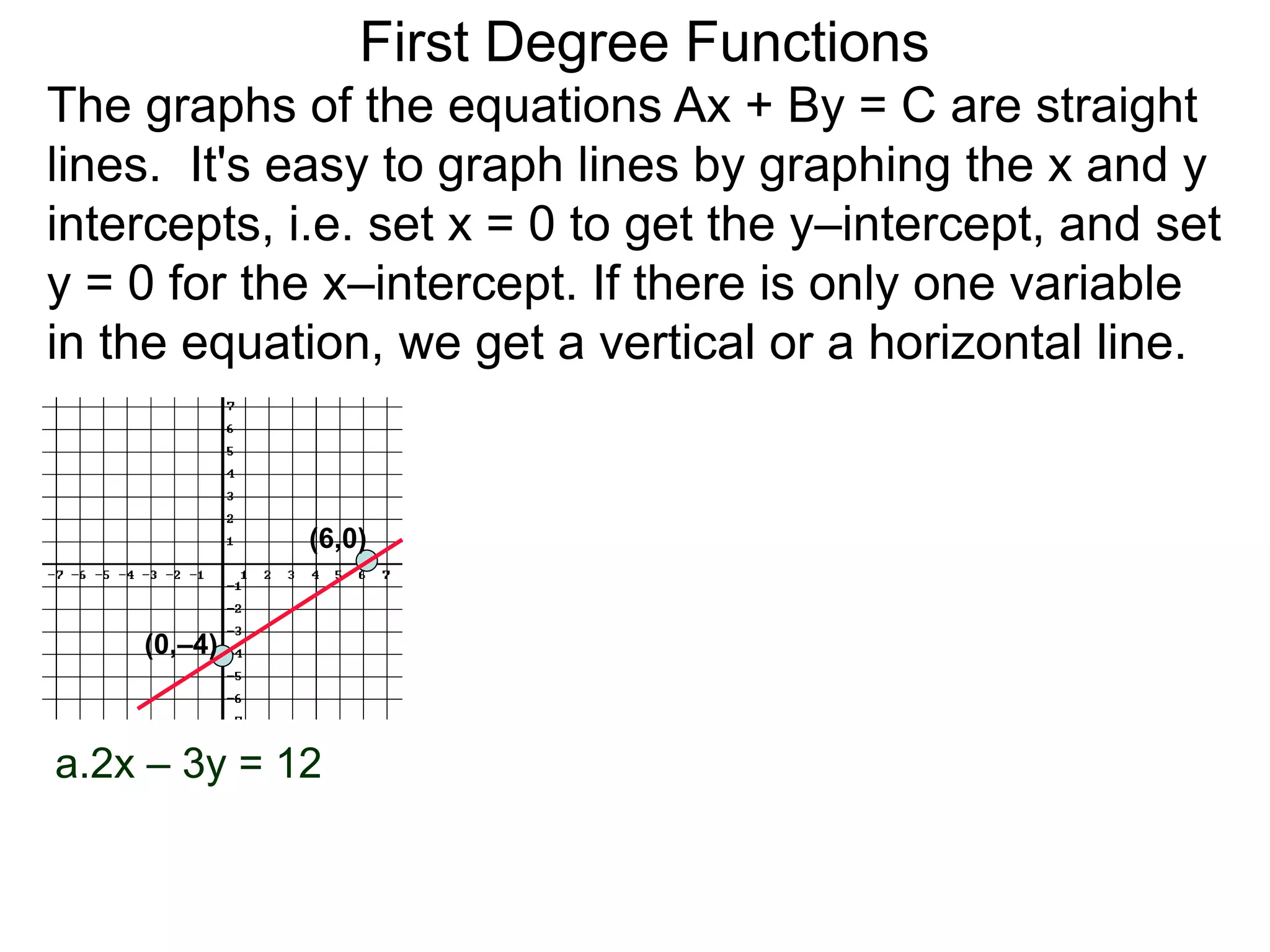
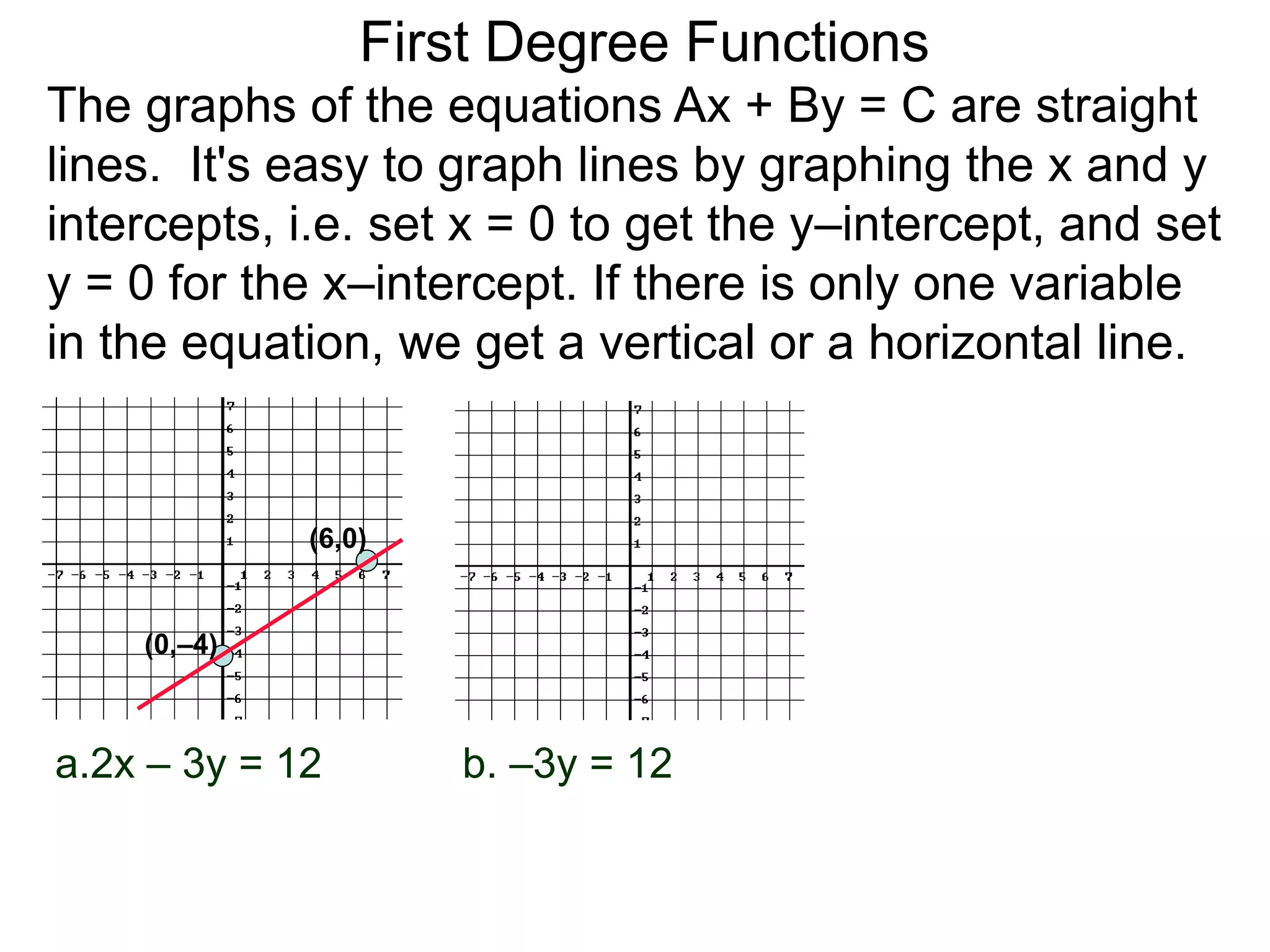
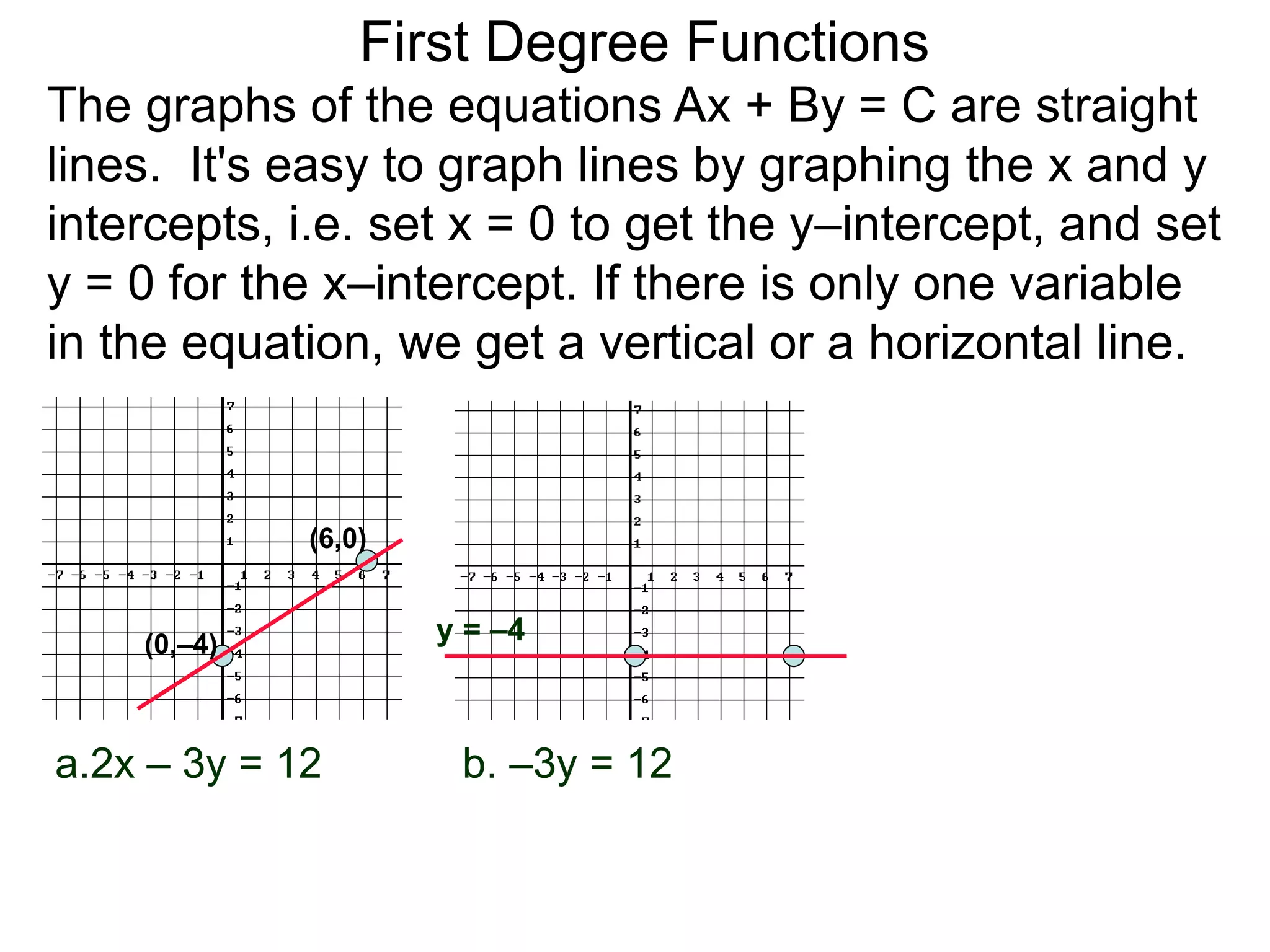
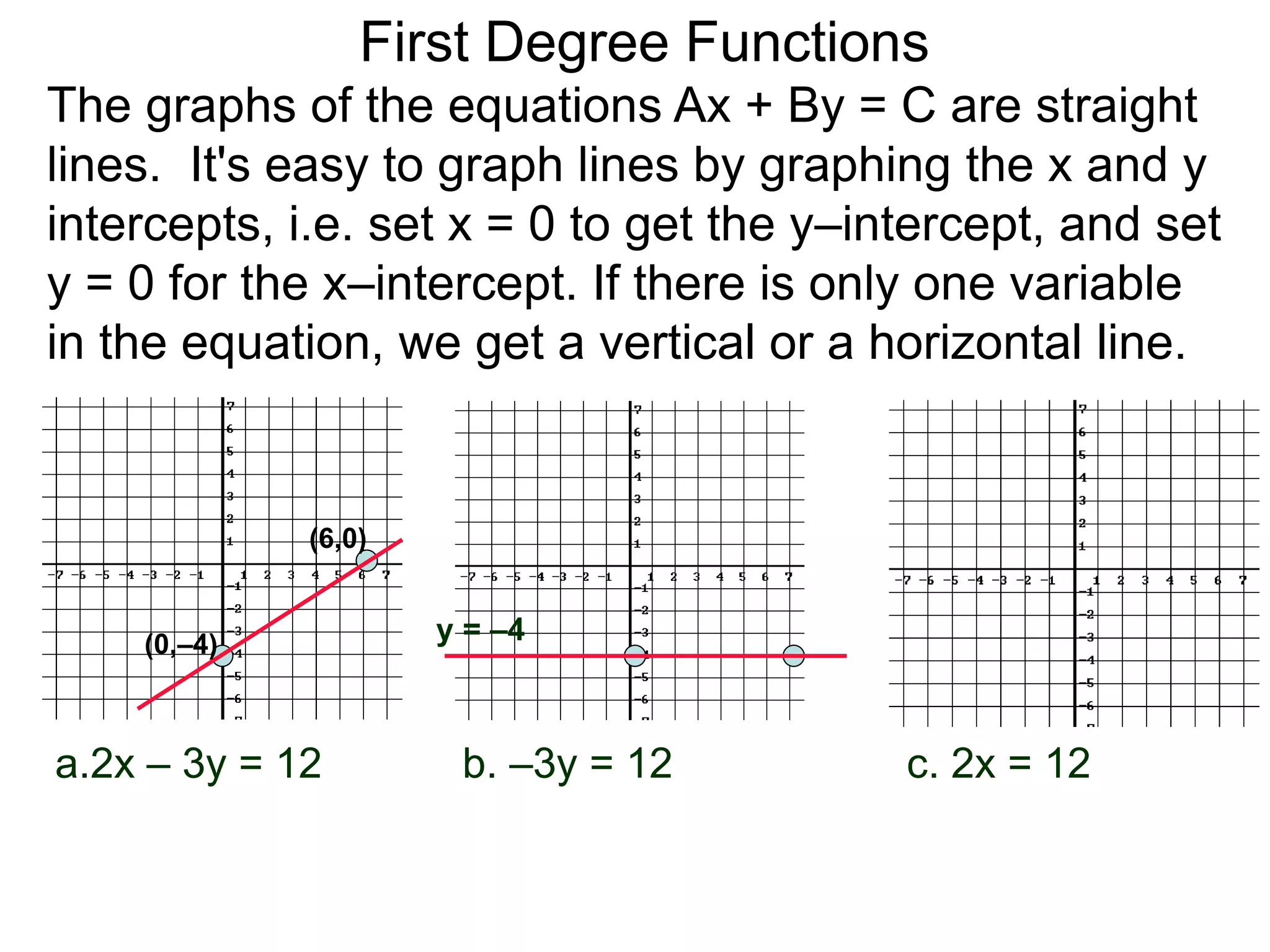
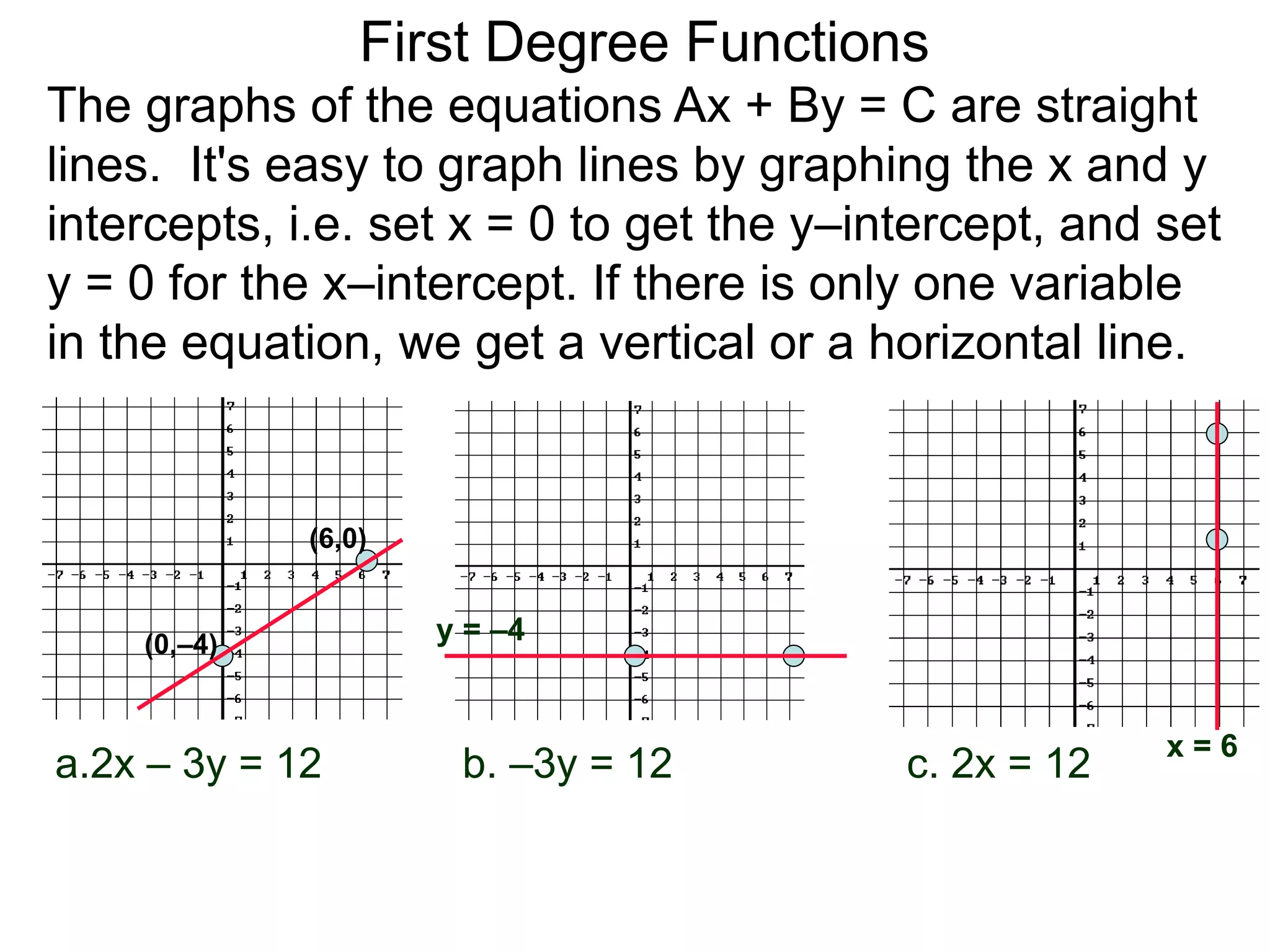
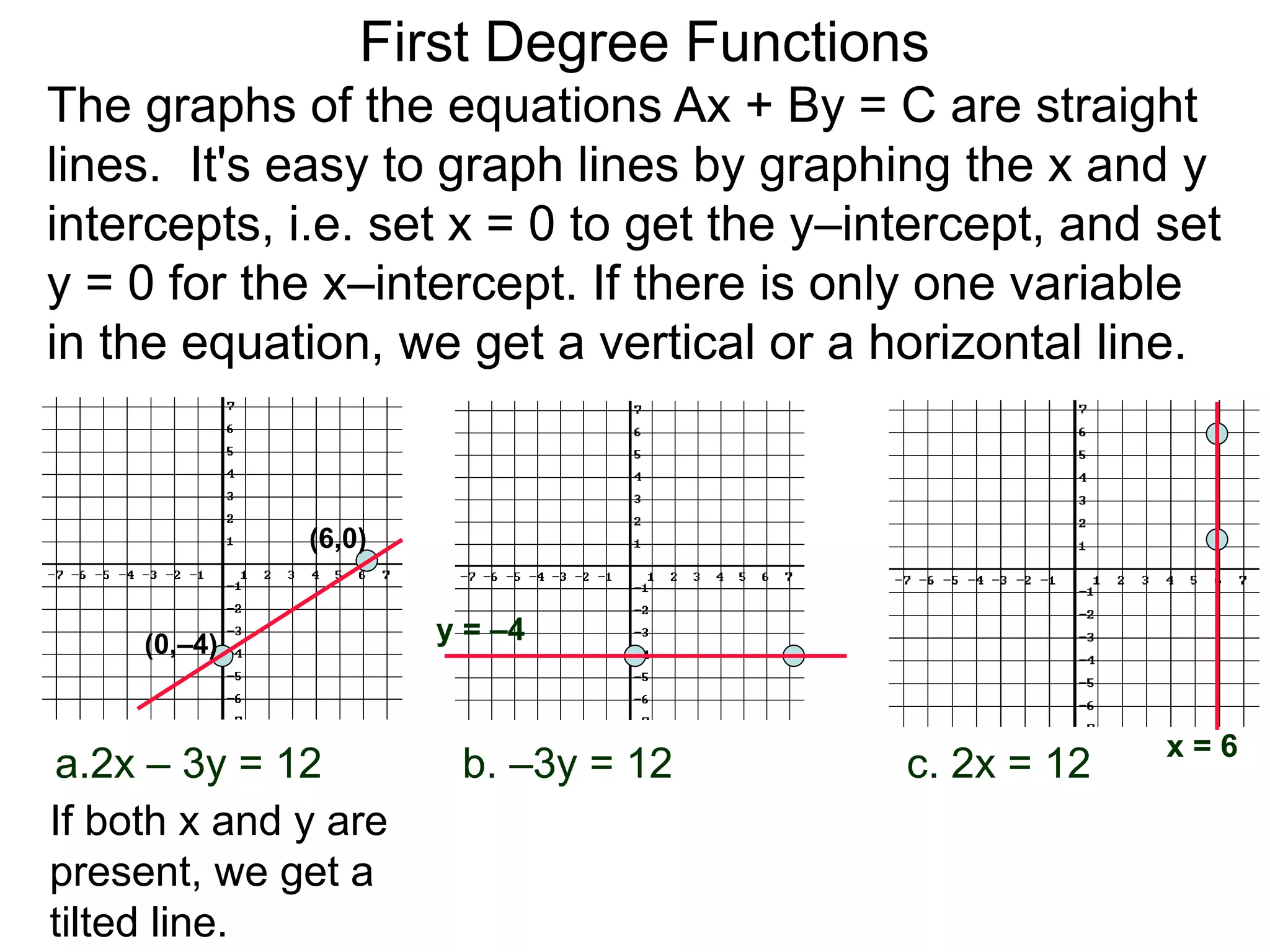
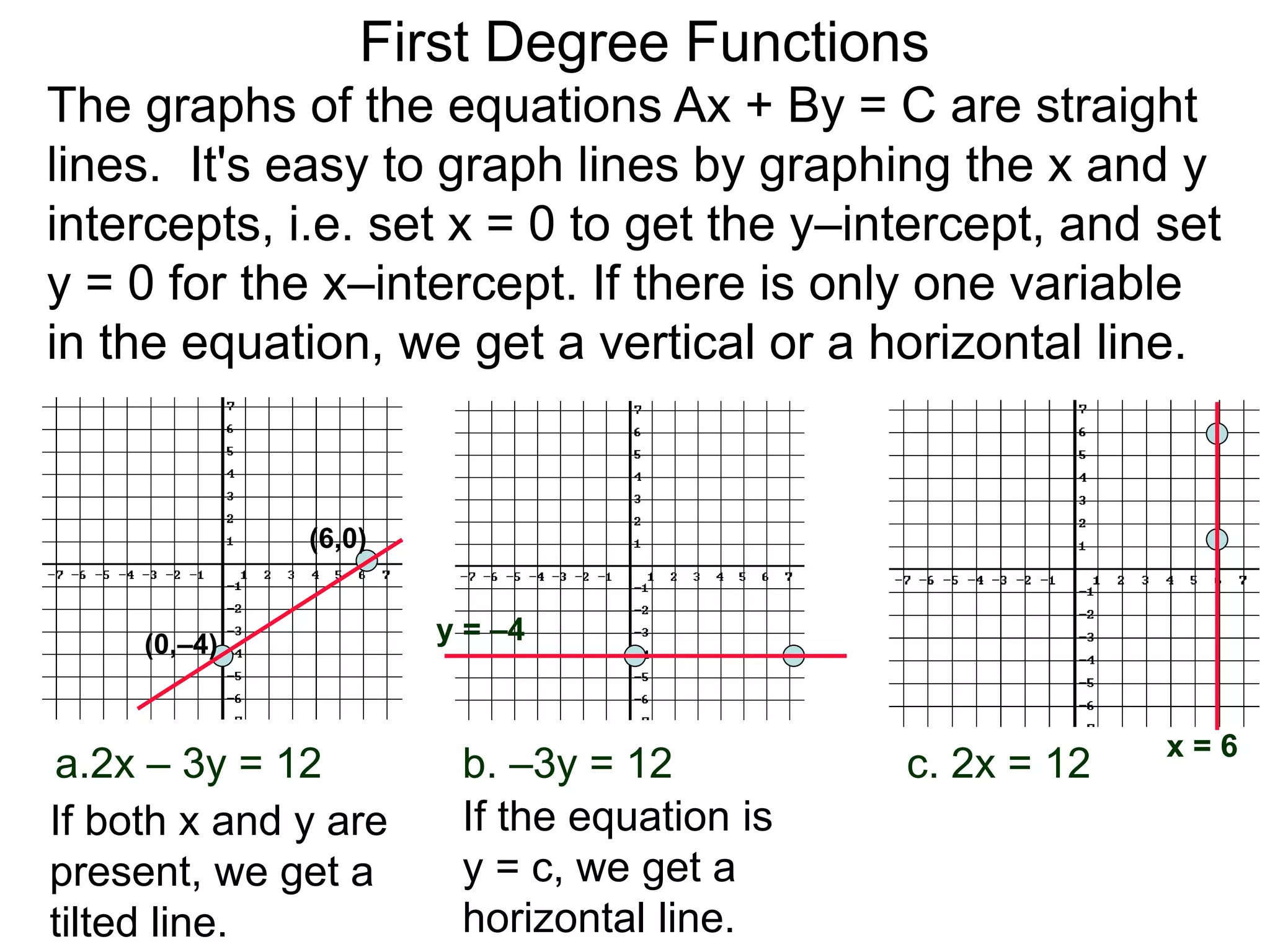
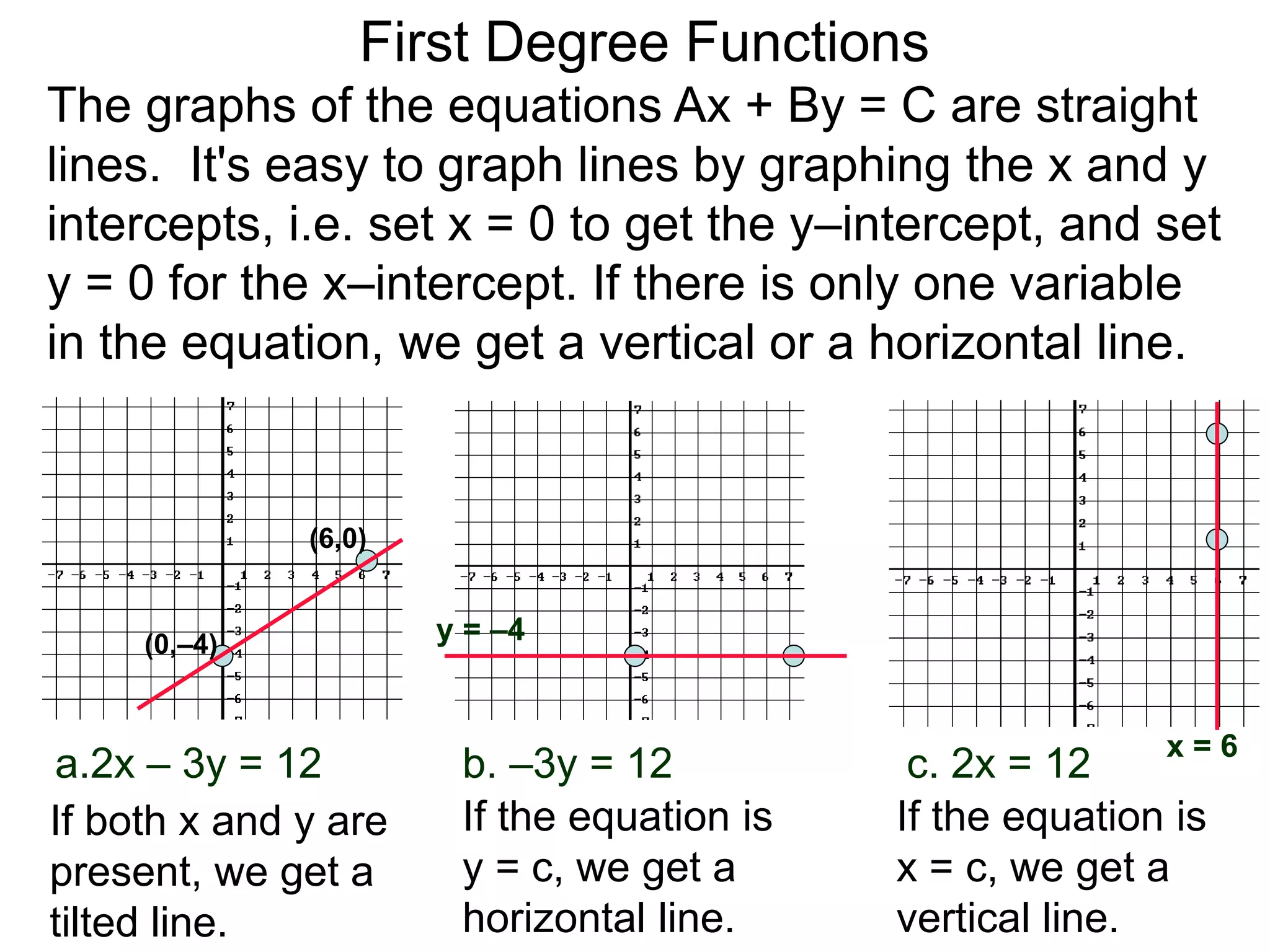
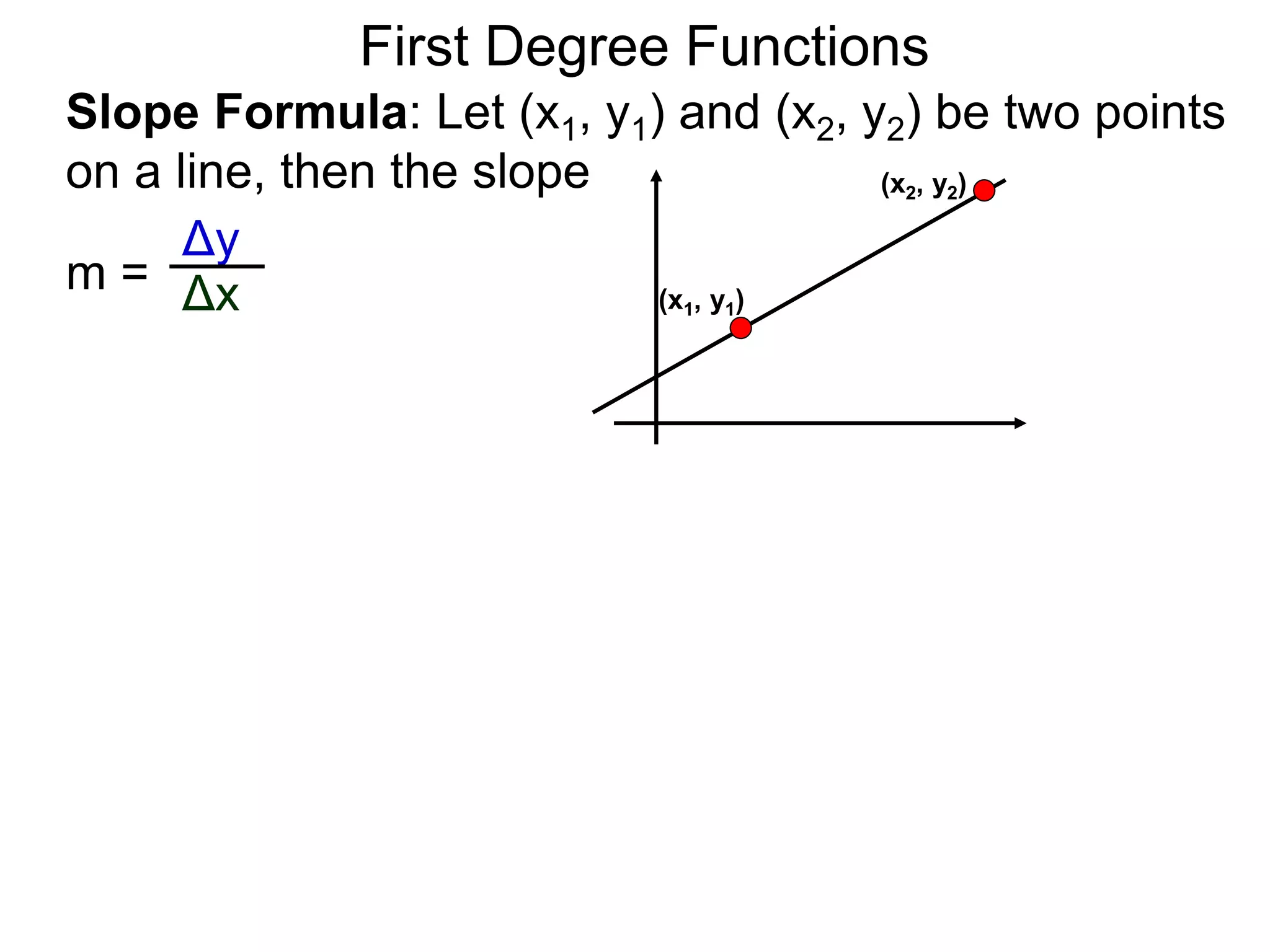
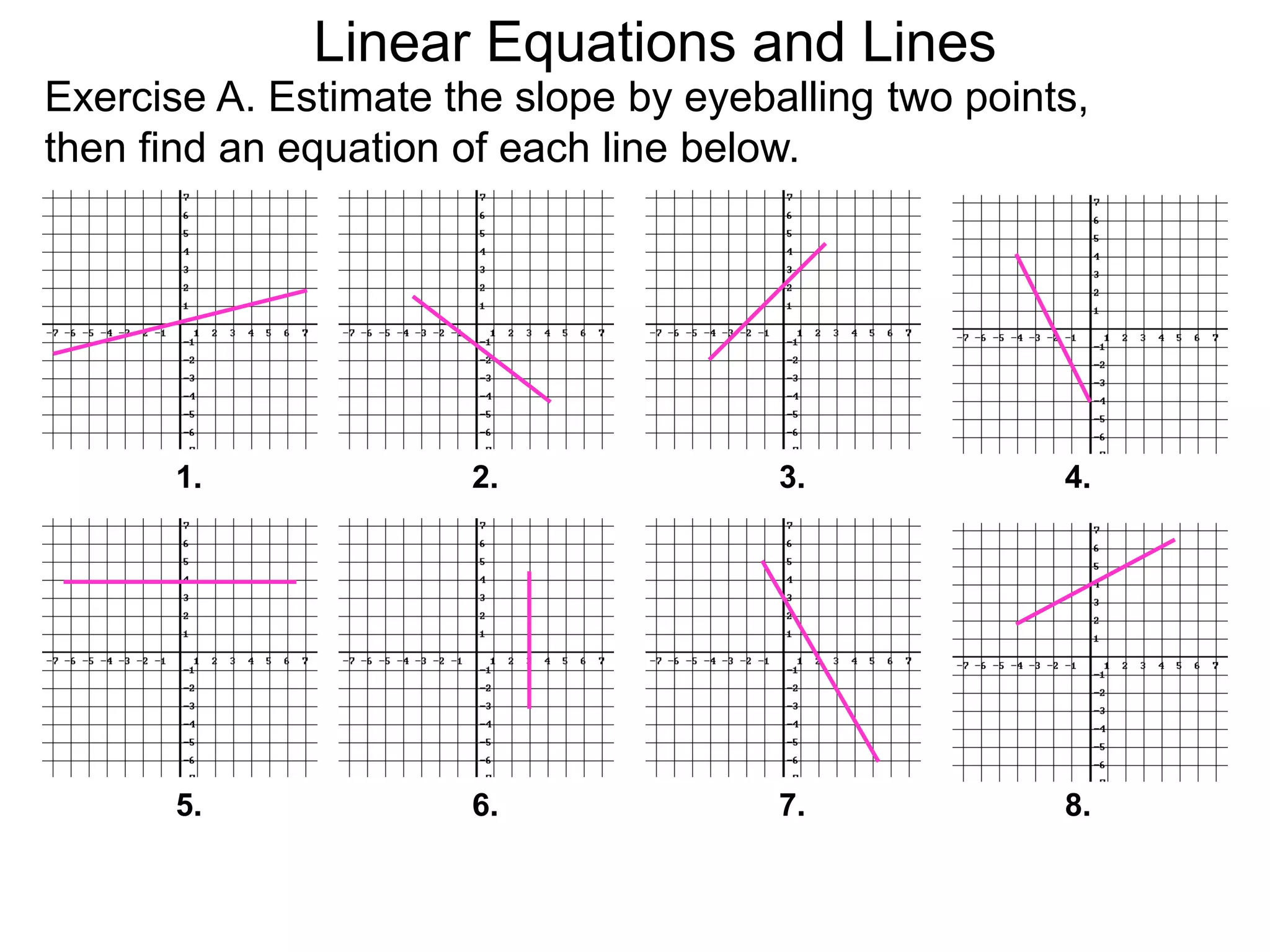
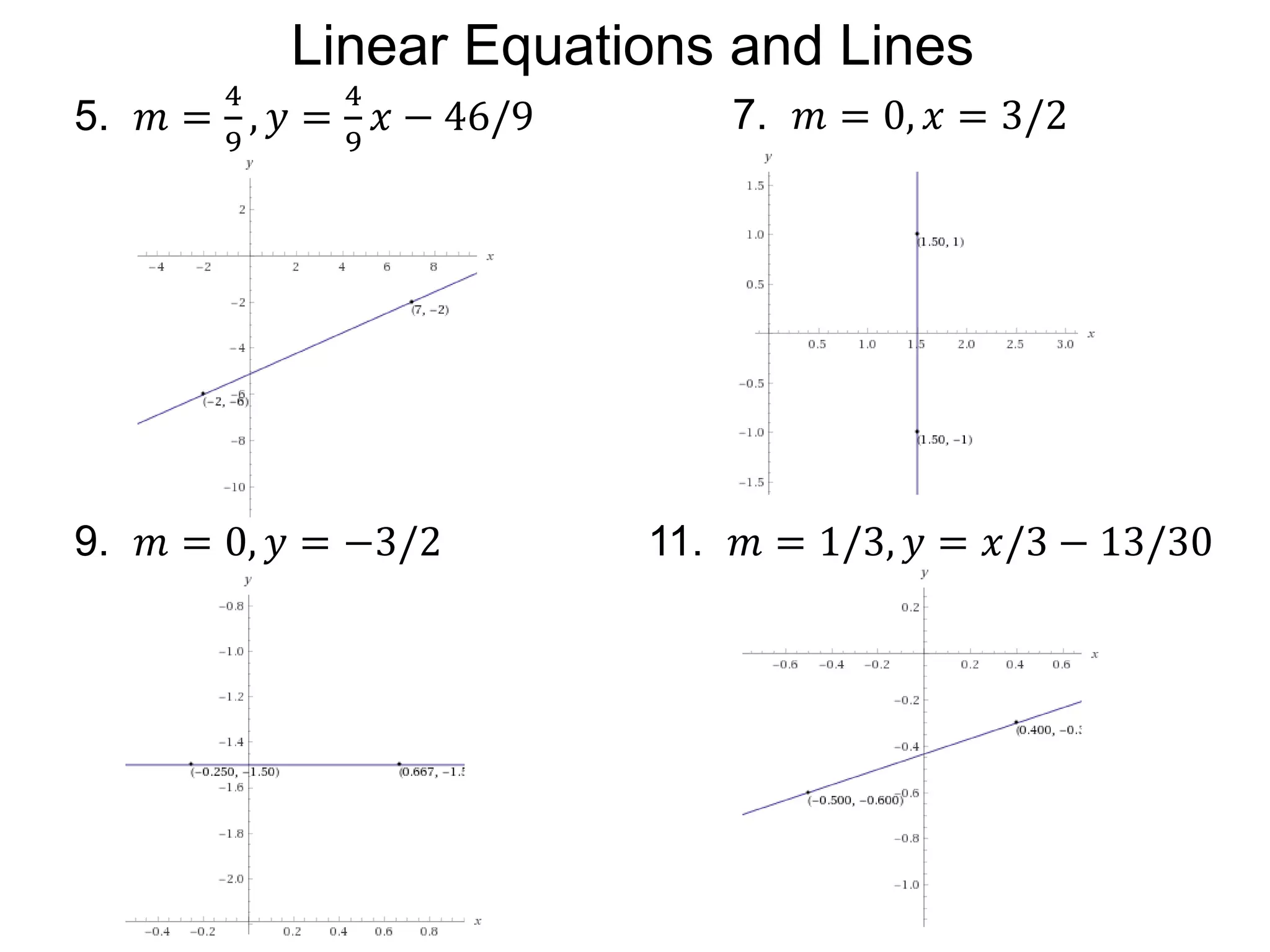
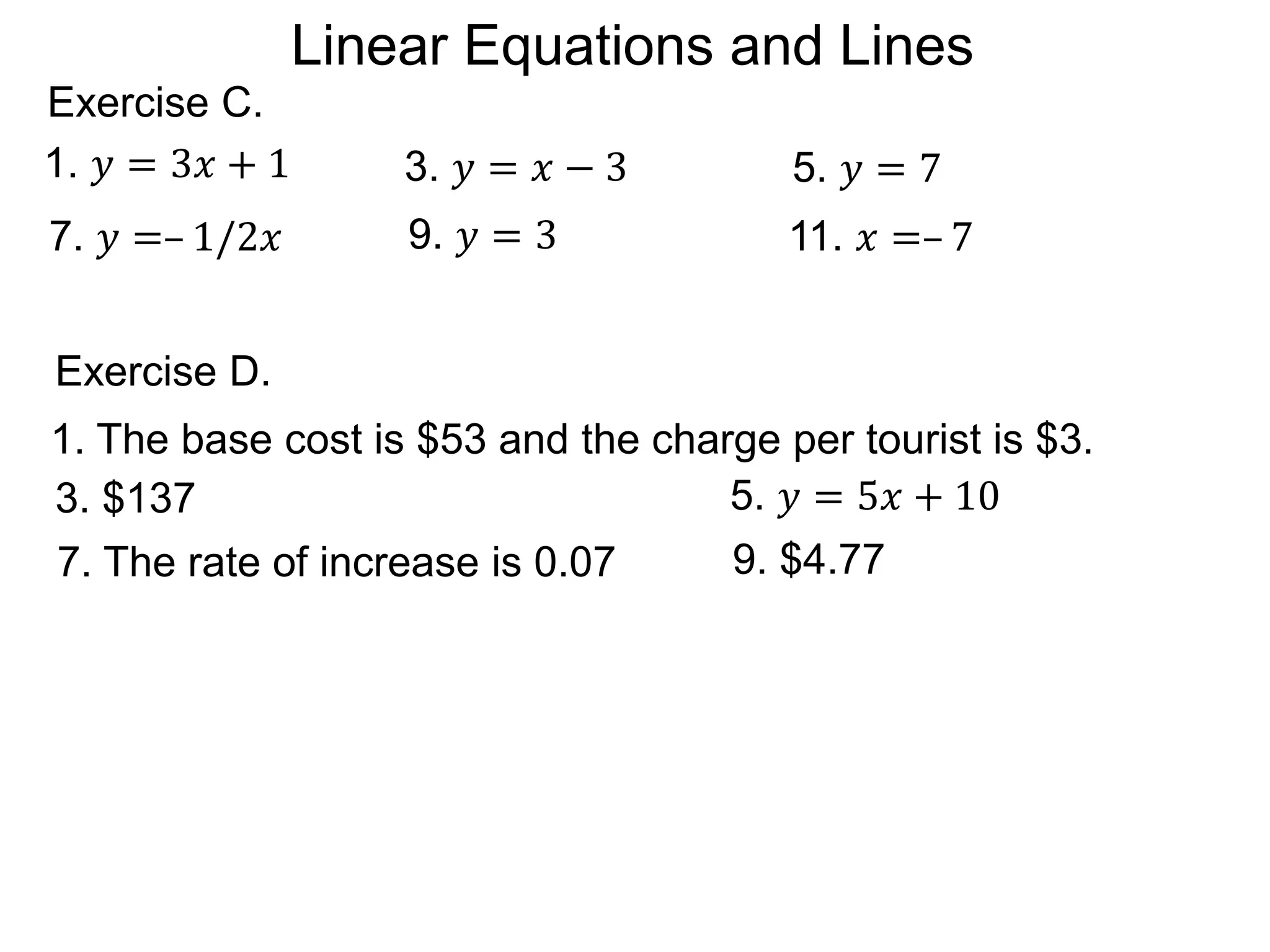The document discusses first degree (linear) functions. It explains that most real-world mathematical functions can be composed of formulas from three groups: algebraic, trigonometric, and exponential-log. Linear functions of the form f(x)=mx+b are especially important, where m is the slope and b is the y-intercept. The graphs of equations of the form Ax+By=C are straight lines. The slope formula for calculating the slope between two points (x1,y1) and (x2,y2) on a line is given as m=(y2-y1)/(x2-x1).