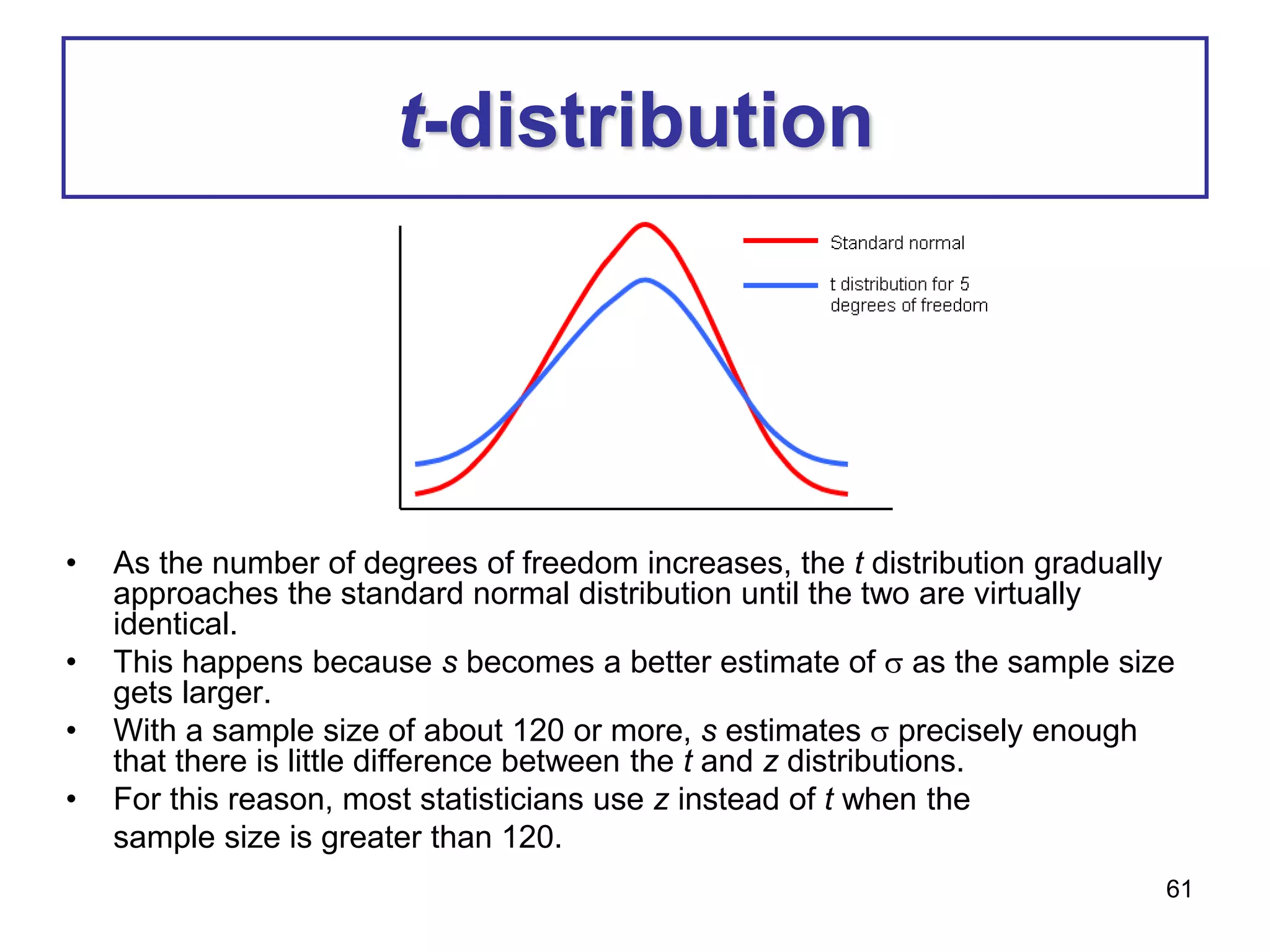
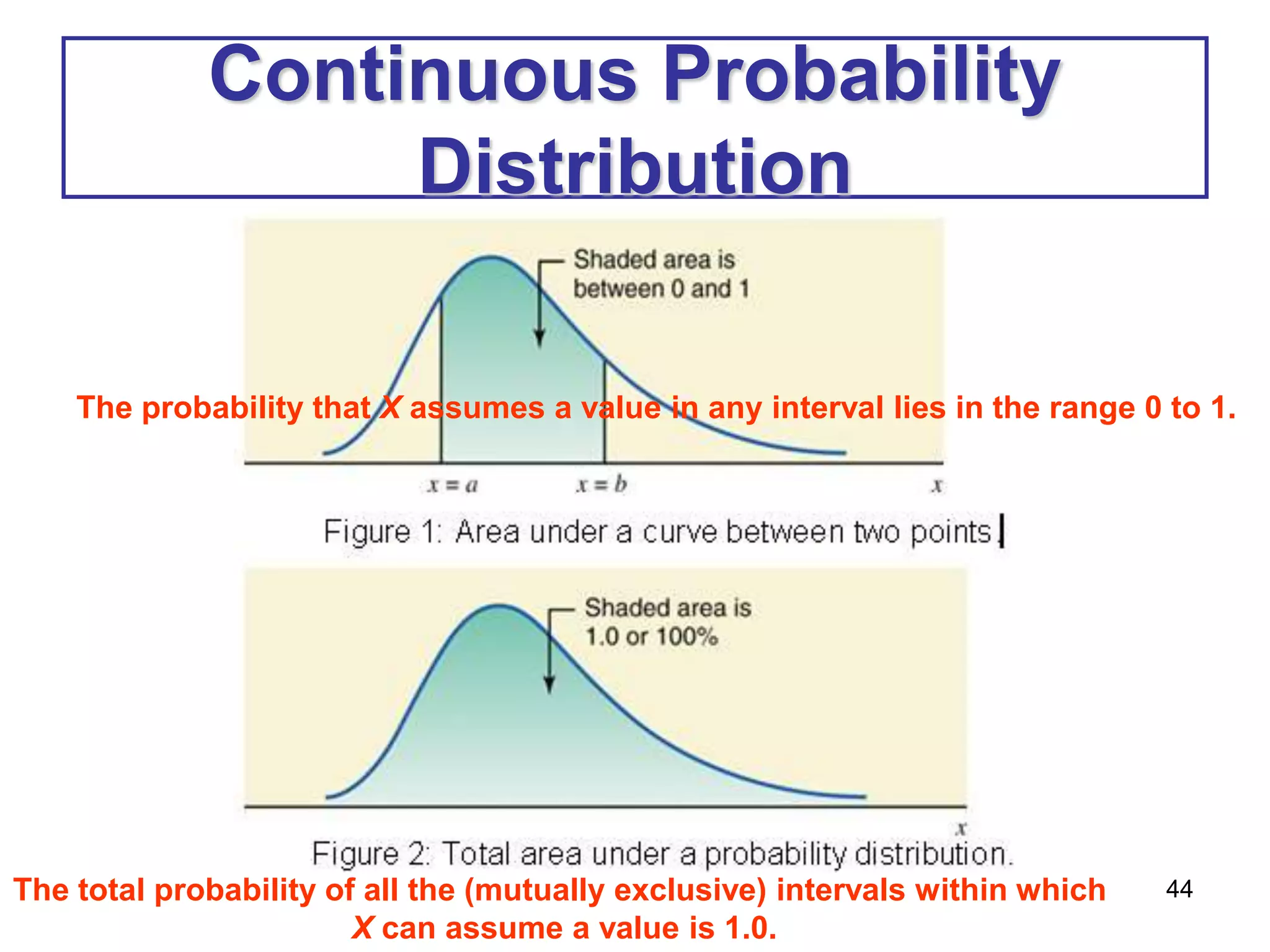
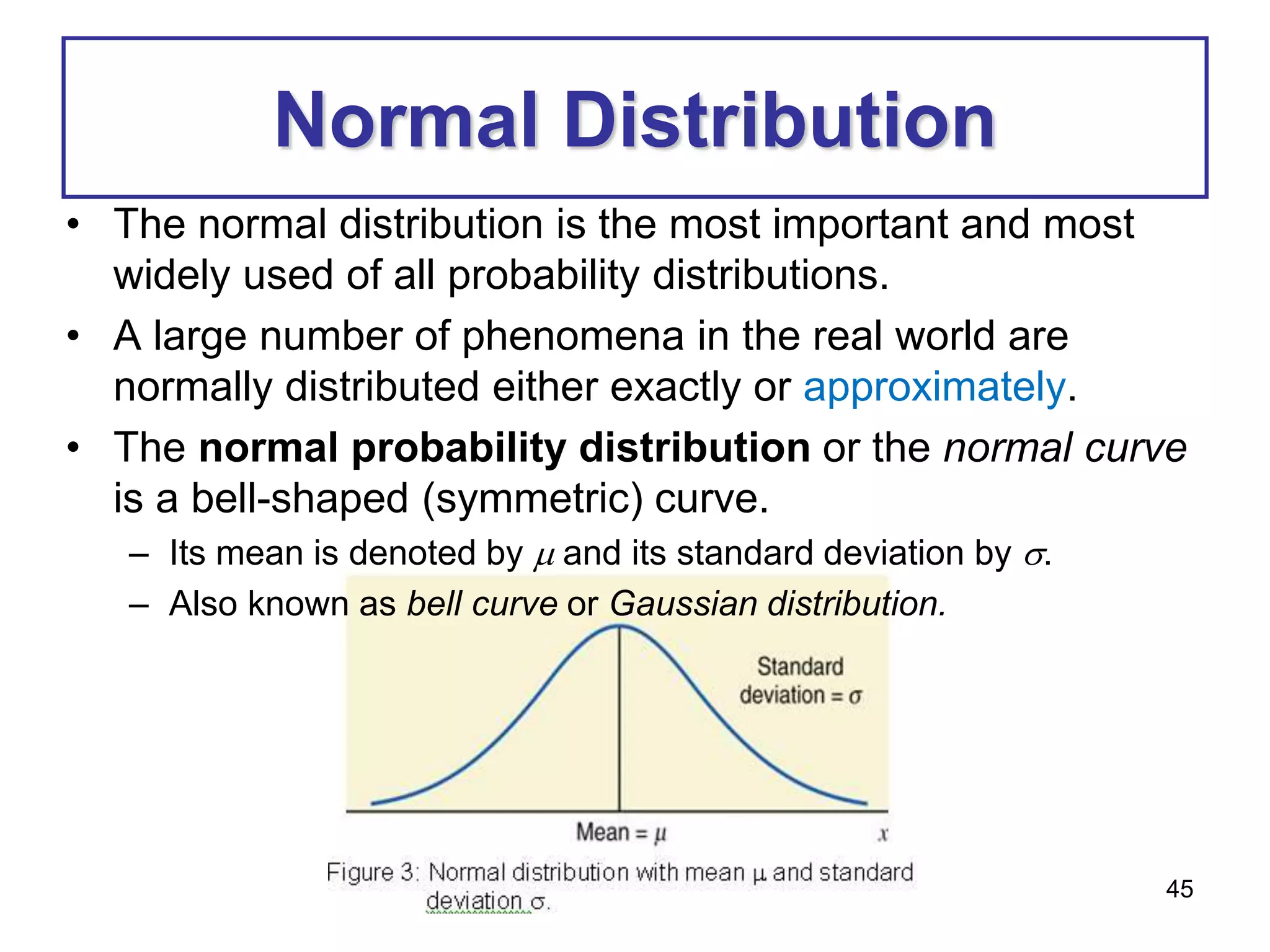
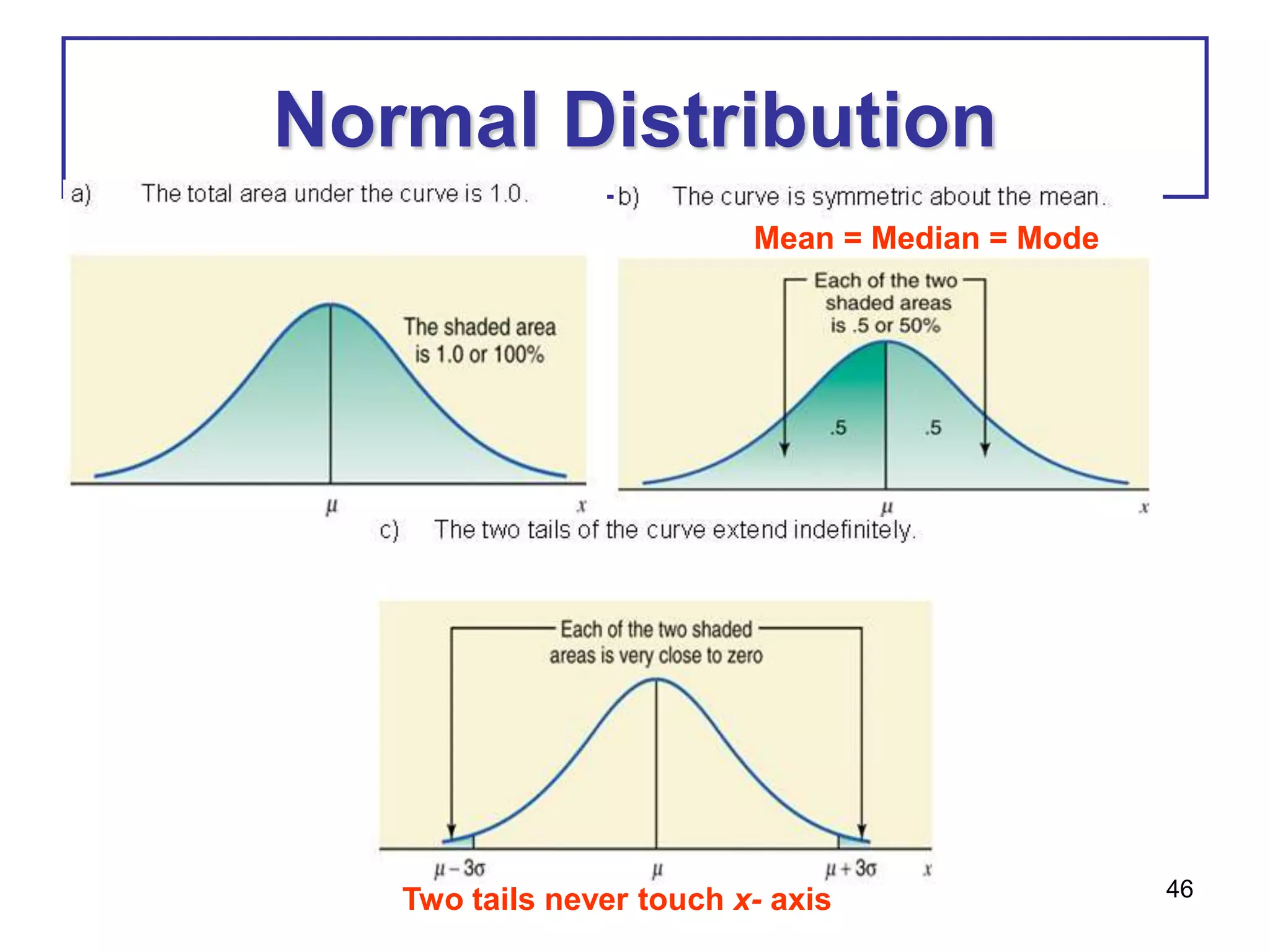
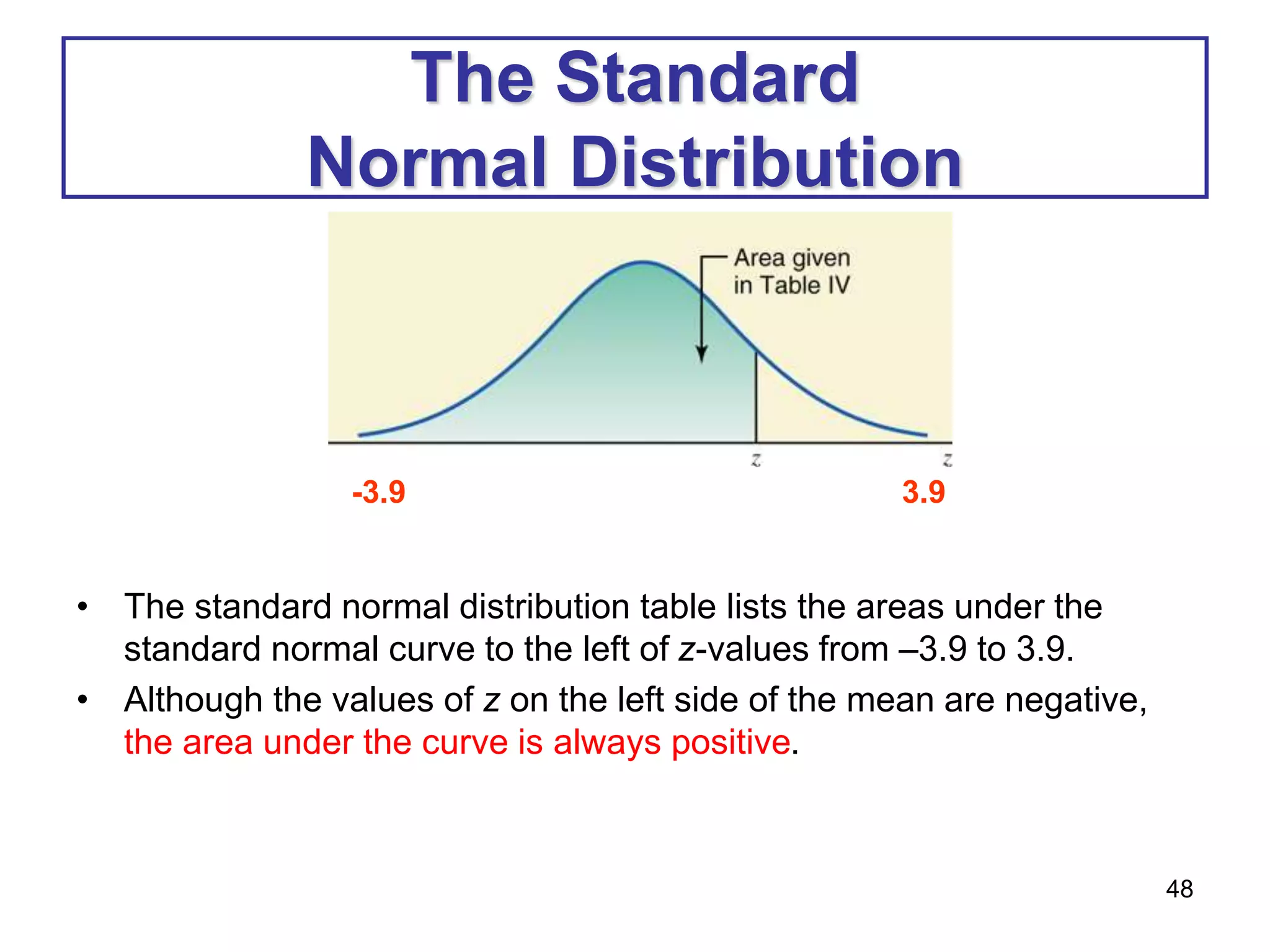
This document provides information about binomial and Poisson distributions. It includes examples of calculating probabilities for binomial distributions using the binomial probability formula and binomial tables. It also provides the key characteristics and formula for the Poisson distribution. The mean, variance and standard deviation are defined for binomial distributions. Examples are provided to demonstrate calculating these values.













































![56
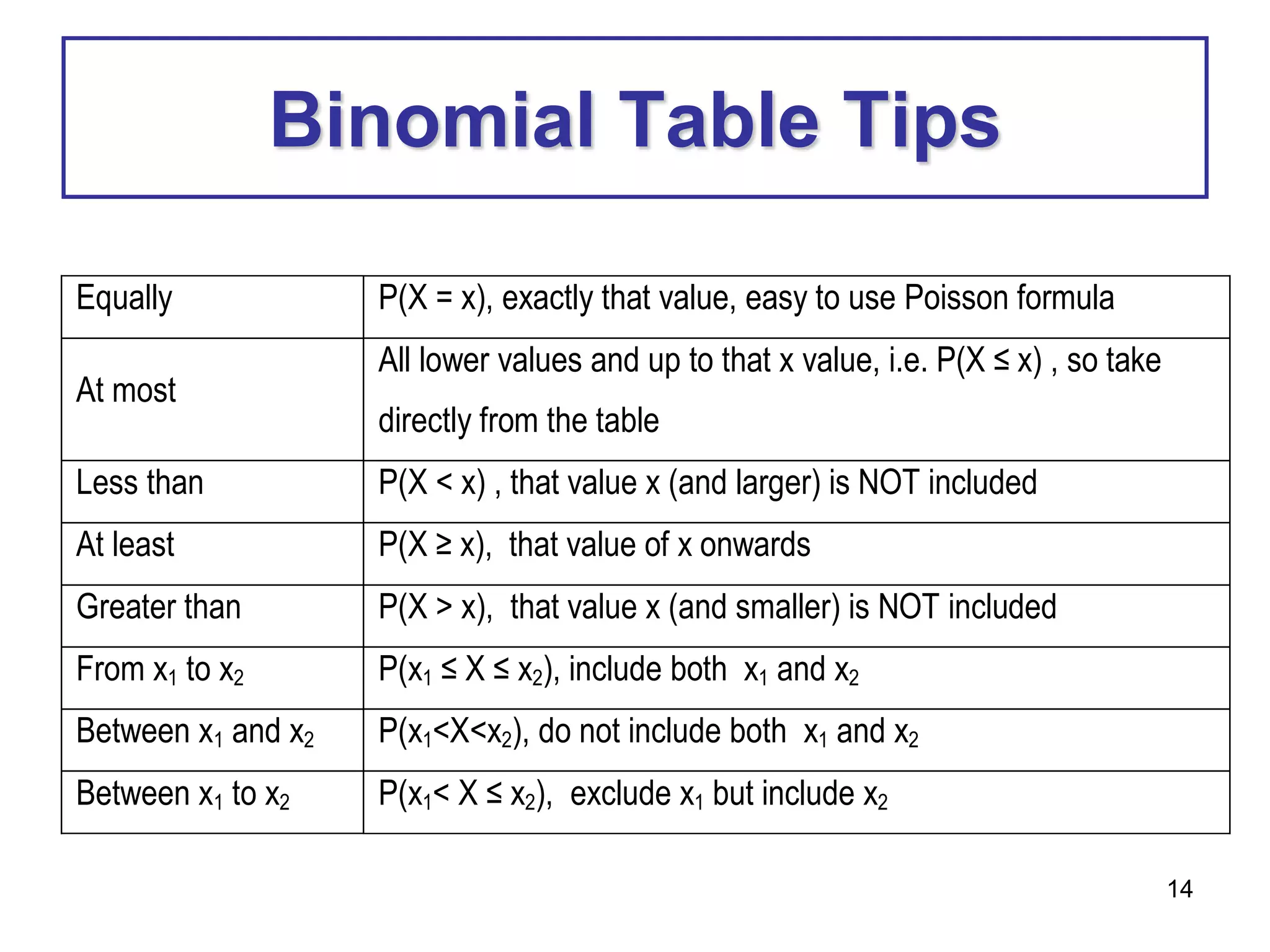
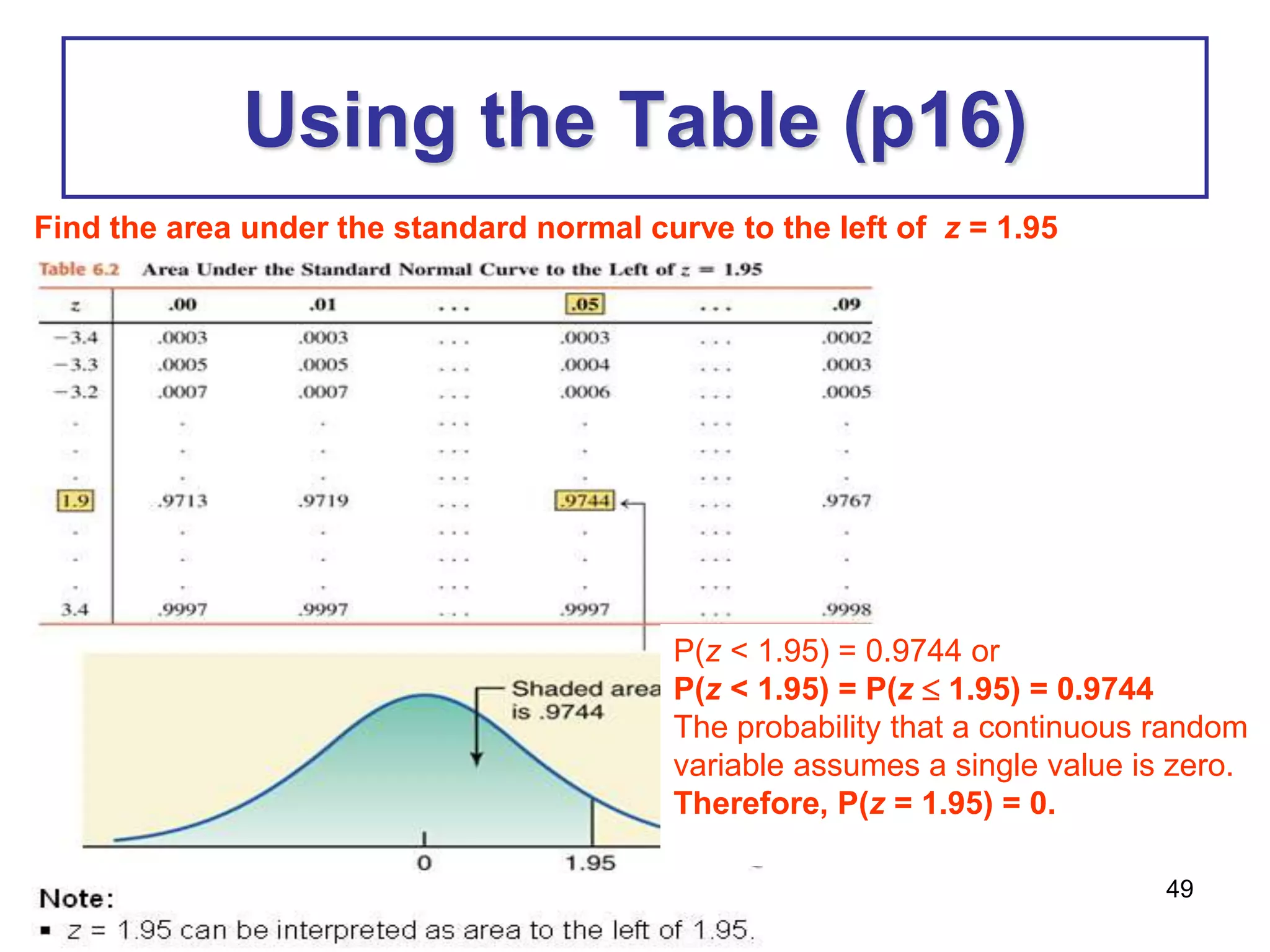
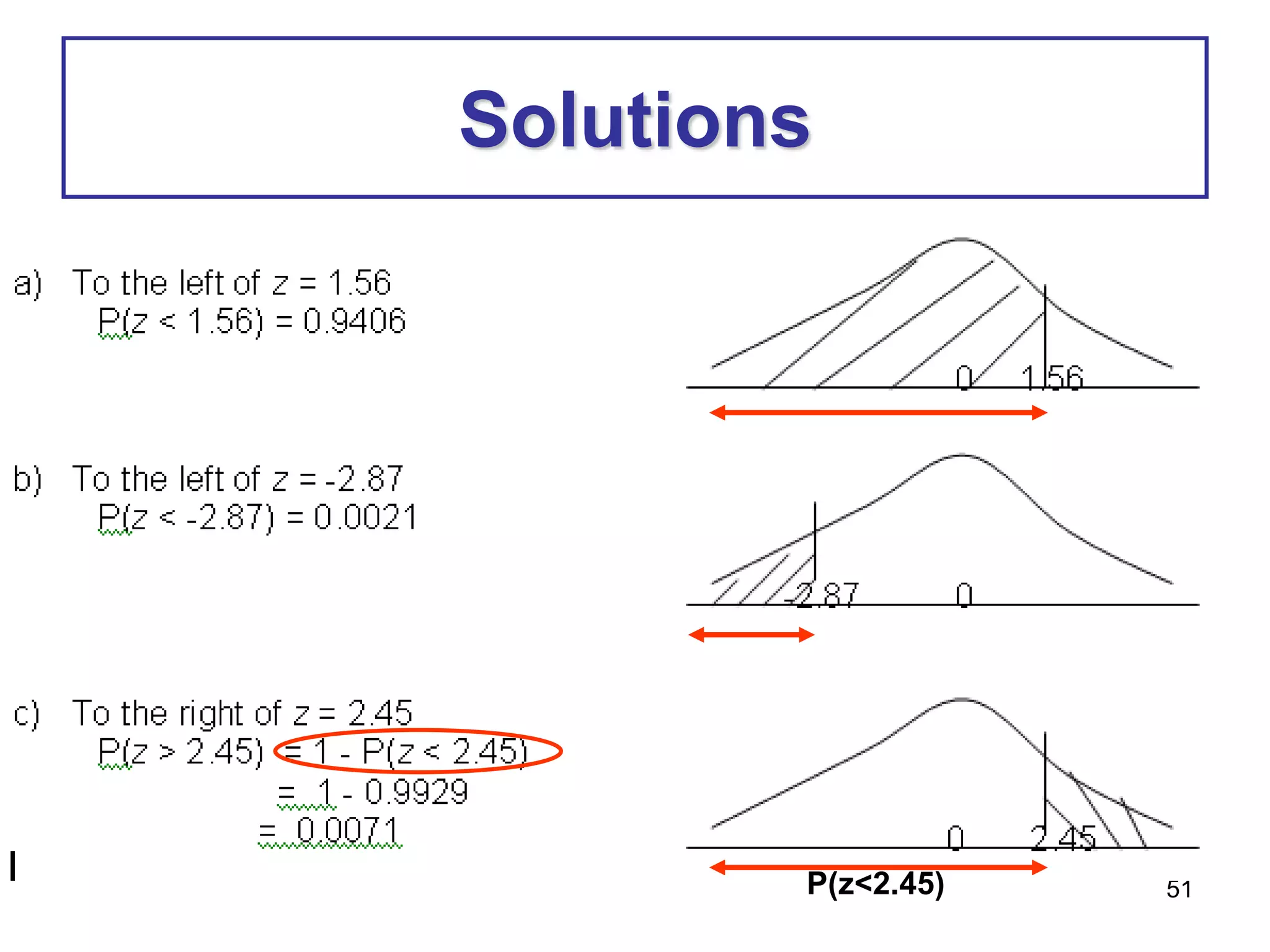
Exercise 5 (p20)
1. Let X denote the time takes to run a road race. Suppose X is
approximately normally distributed with mean of 190 minutes and
standard deviation of 21 minutes. If one runner is selected at
random, what is the probability that this runner will complete this
road race:
a) in less than 150 minutes?
b) in 205 to 245 minutes?
P(X < 150) = P(z < 150 - 190)
21
= P(z < -1.9)
= 0.0287
P(205 < X < 245) = P[(205-190 )<z < 245 - 190)]
21 21
= P(0.71 <z < 2.62)
= P(z < 2.62) - P(z < 0.71)
= 0.9956 – 0.7611
= 0.2345](https://image.slidesharecdn.com/chapter5-221210150540-e109ff33/75/Chapter-5-pptx-56-2048.jpg)


![59
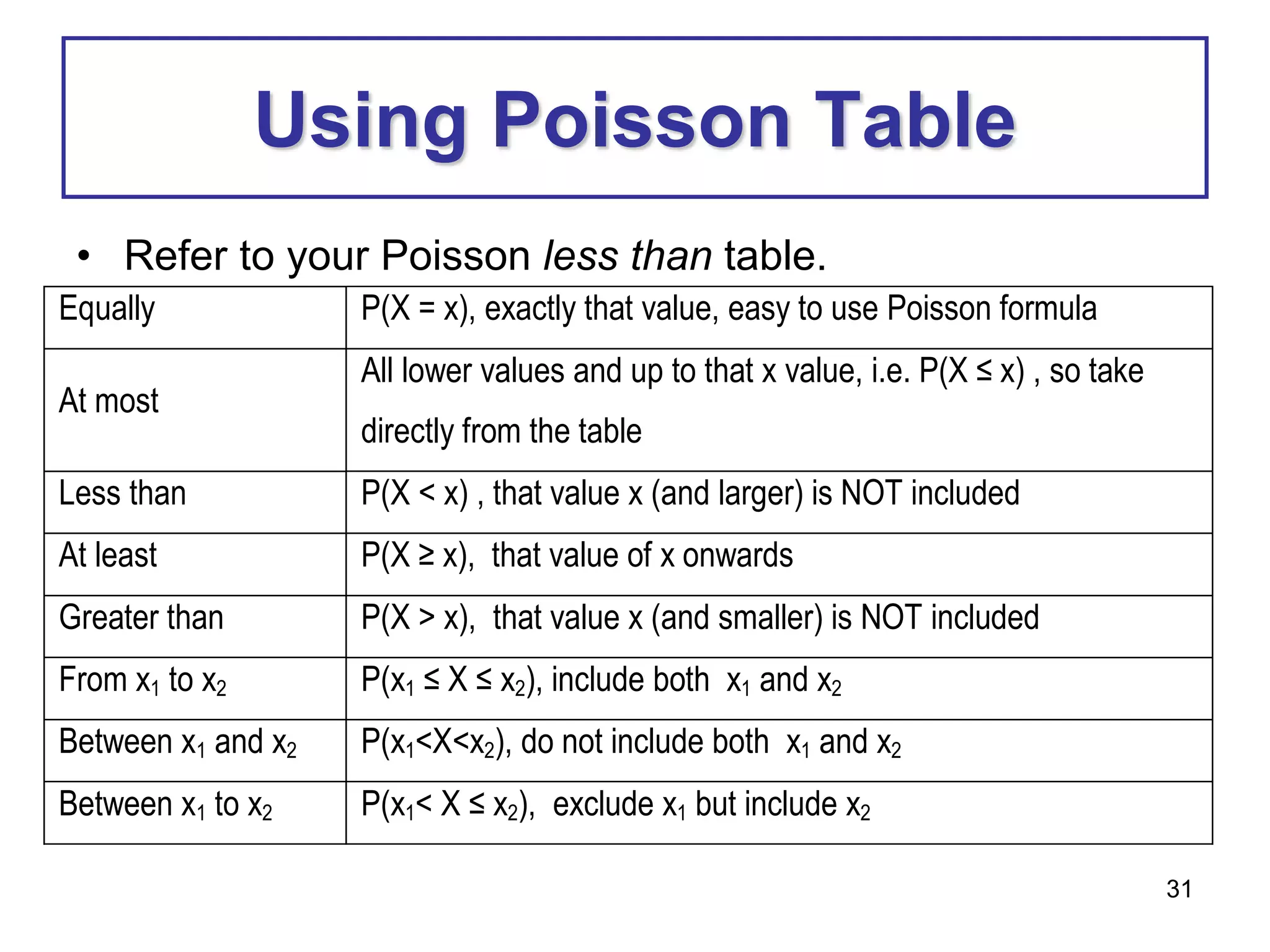
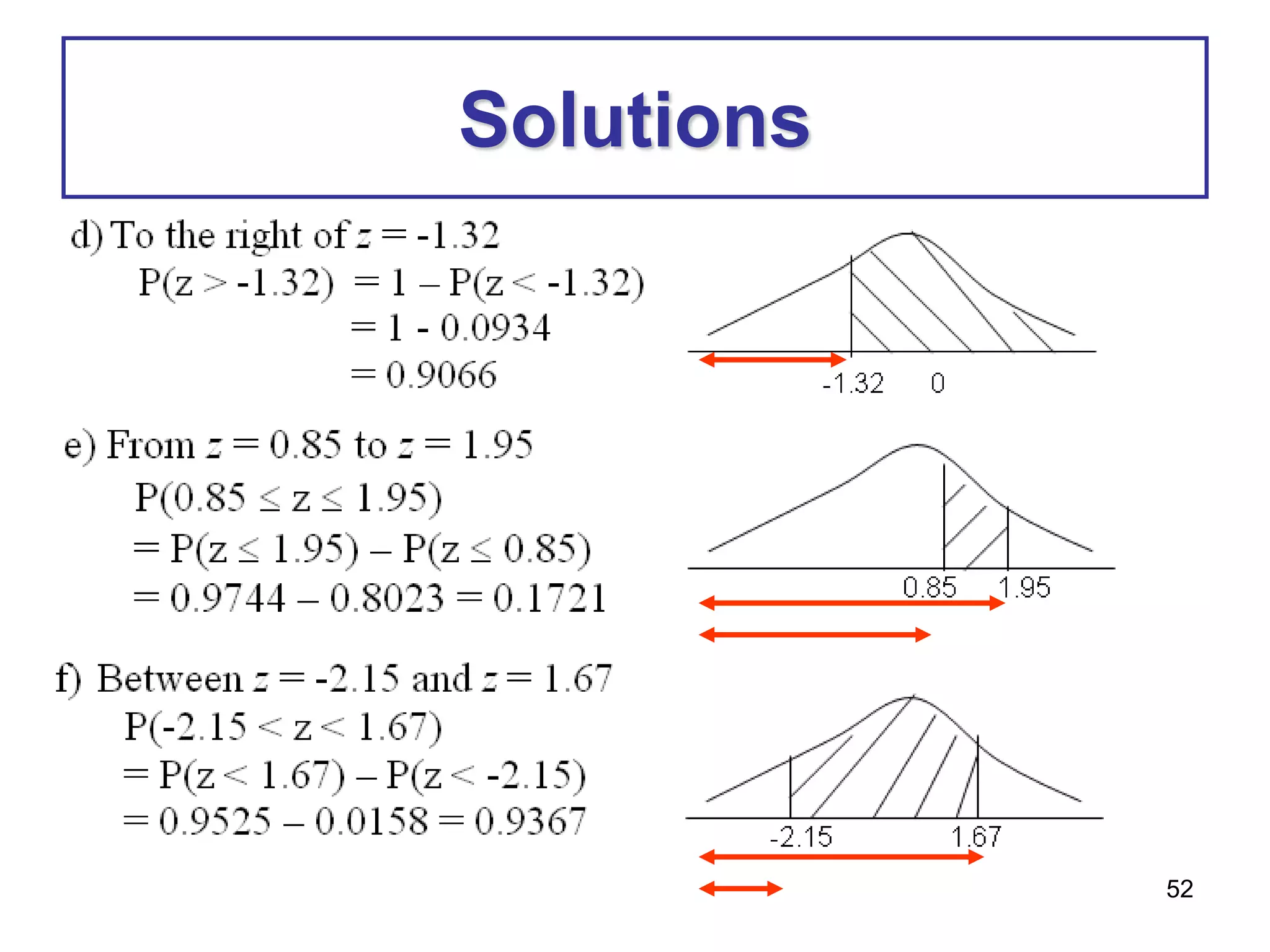
Exercise 5
b) Calculate the probability that a candidate selected at random has a
score between 45 and 65
P(45 < X < 65) = P[(45 – 55) <z < 65 – 55)]
10 10
= P( -1 < z < 1)
= P (z<1) – P(z<-1)
= 0.8413 – 0.1587
= 0.6826
= 10
µ = 55 65
45
z
µ = 0
- values + values
1
-1](https://image.slidesharecdn.com/chapter5-221210150540-e109ff33/75/Chapter-5-pptx-59-2048.jpg)