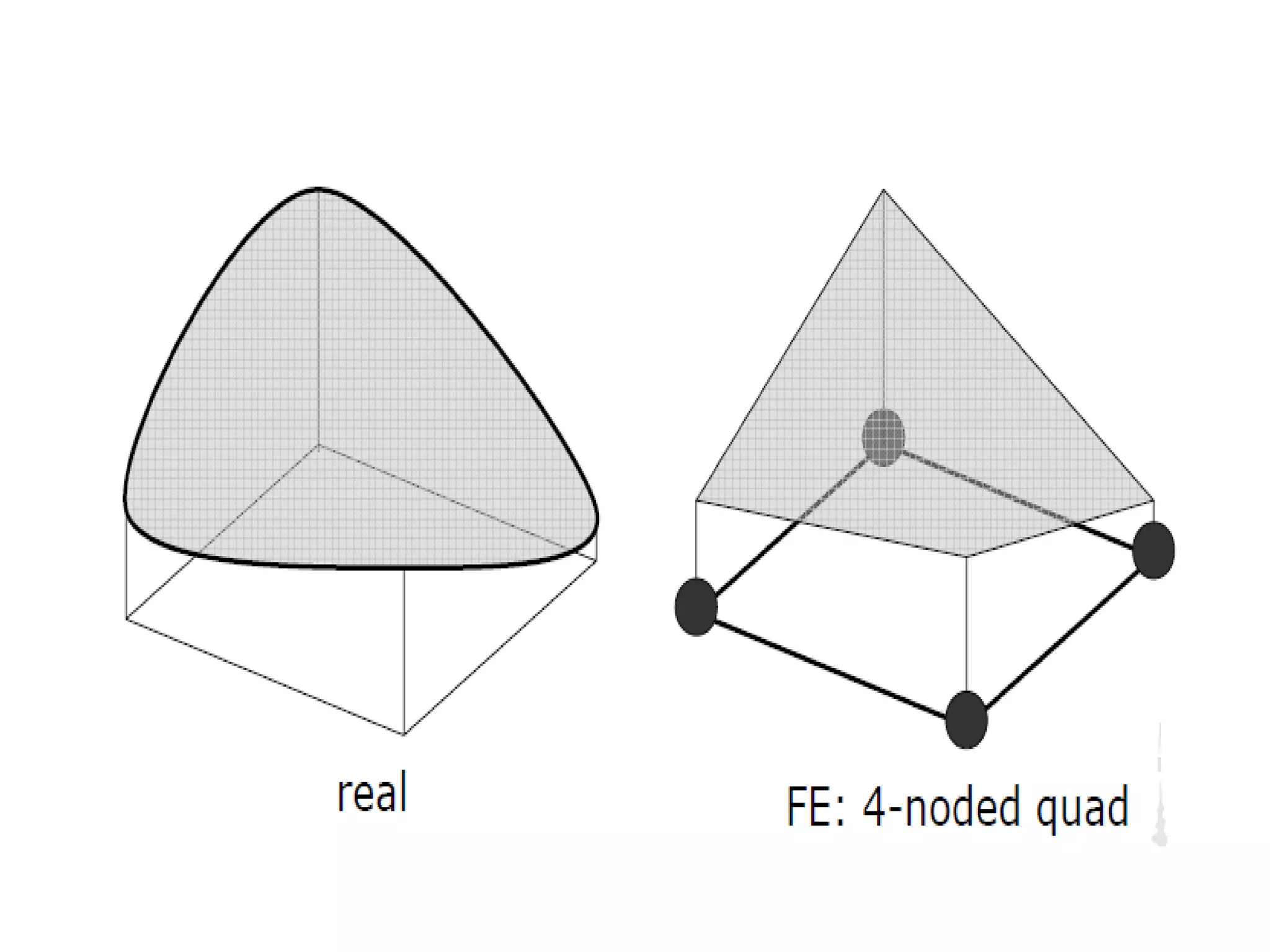
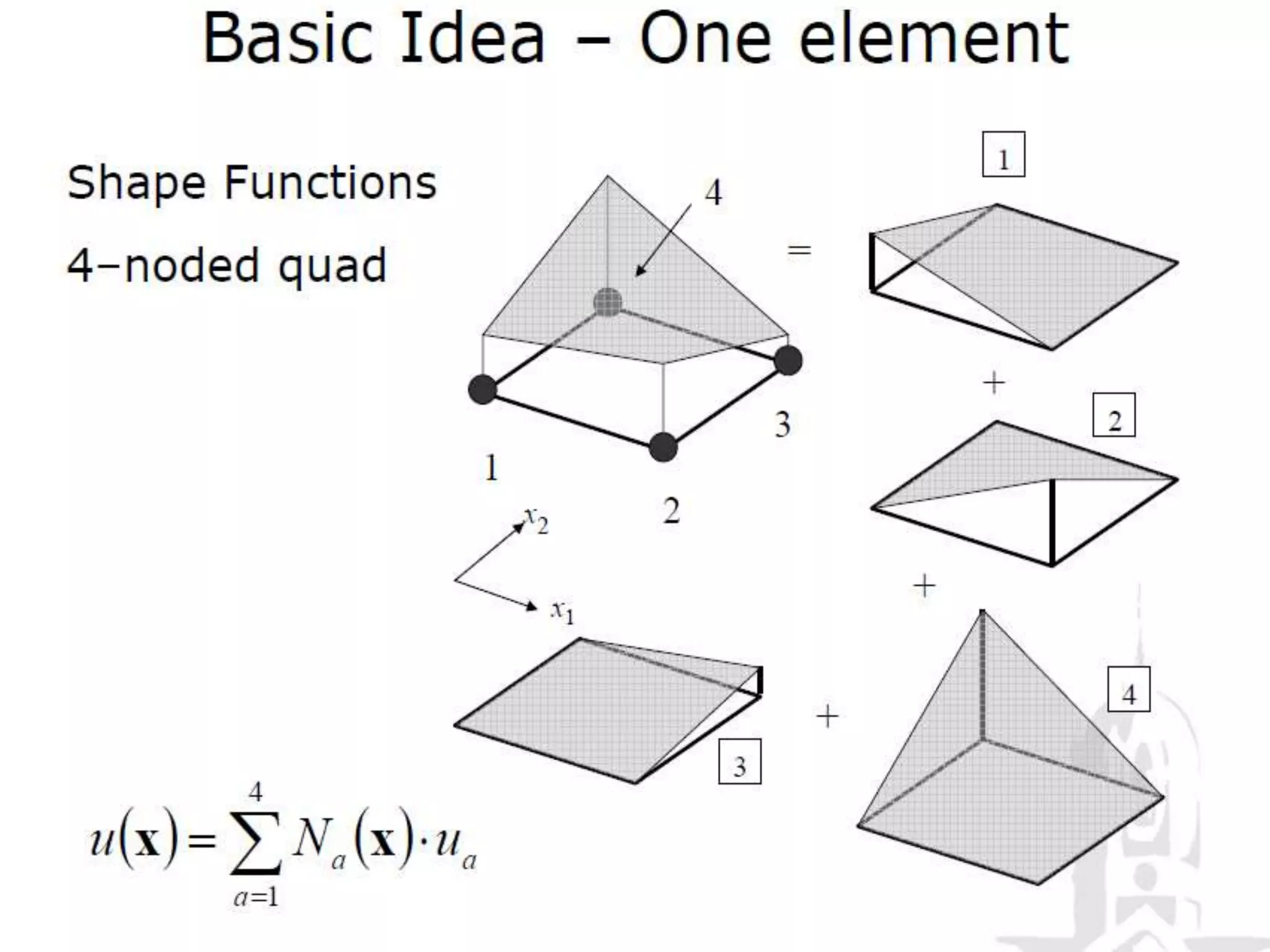
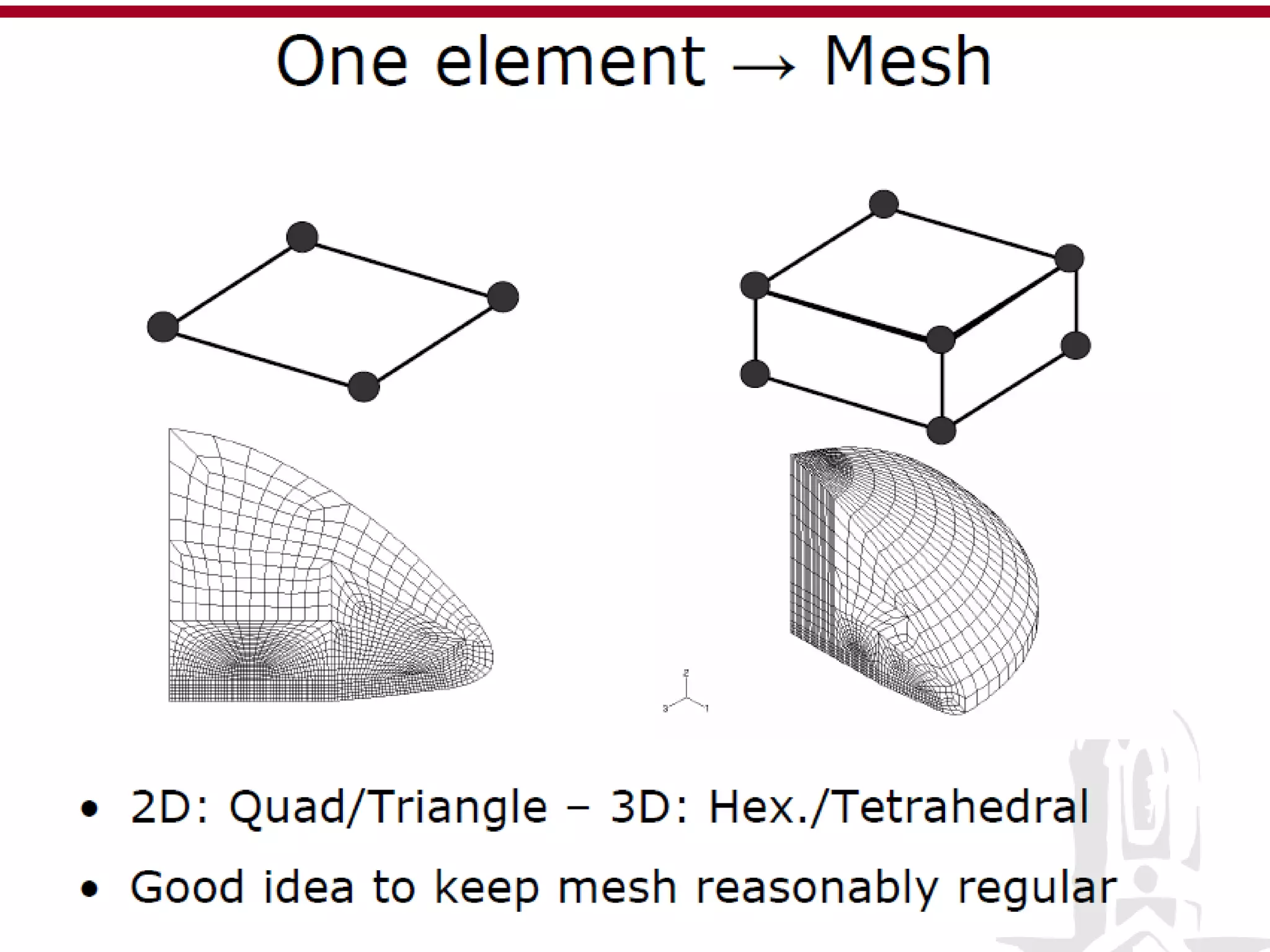
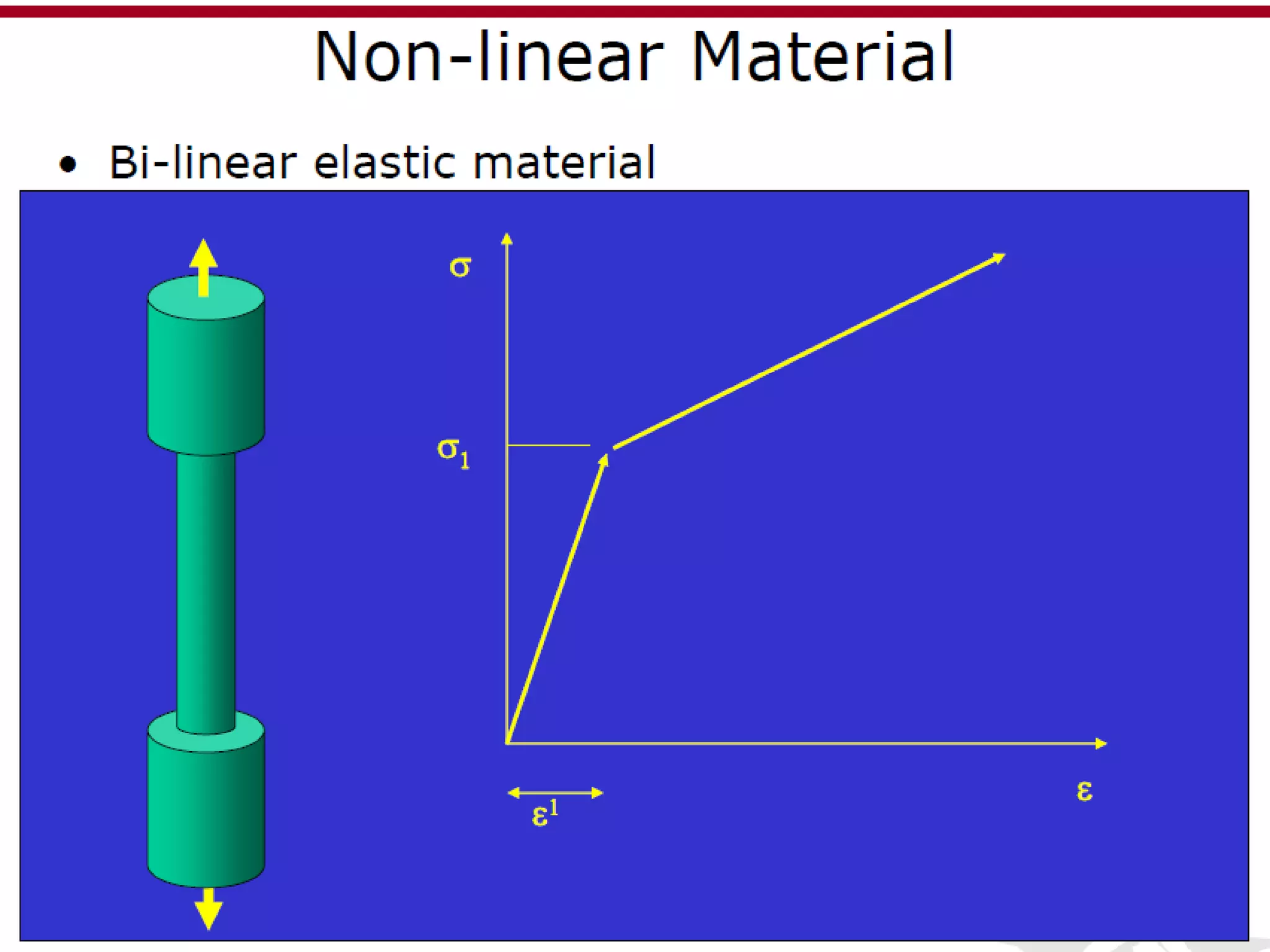
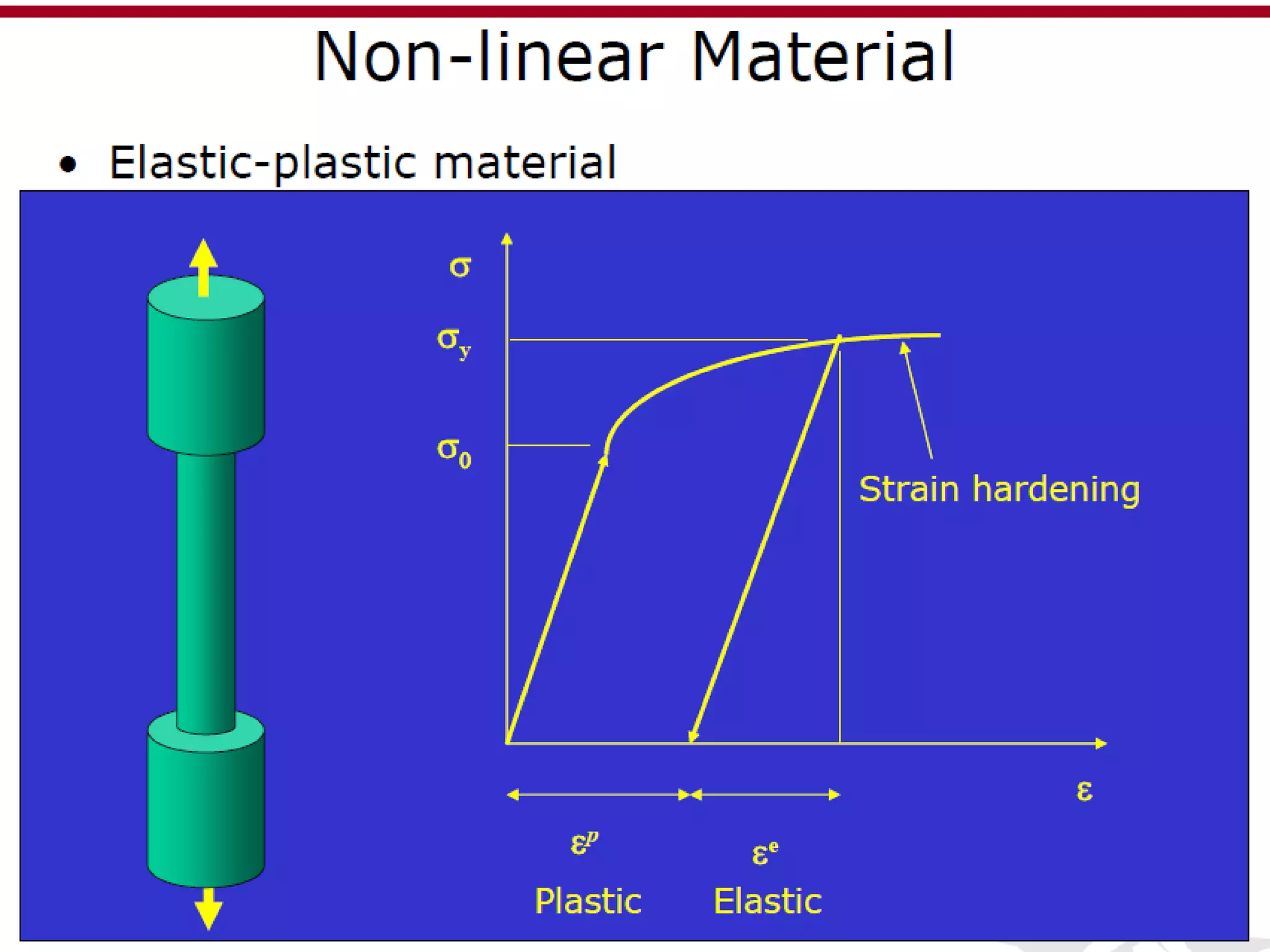
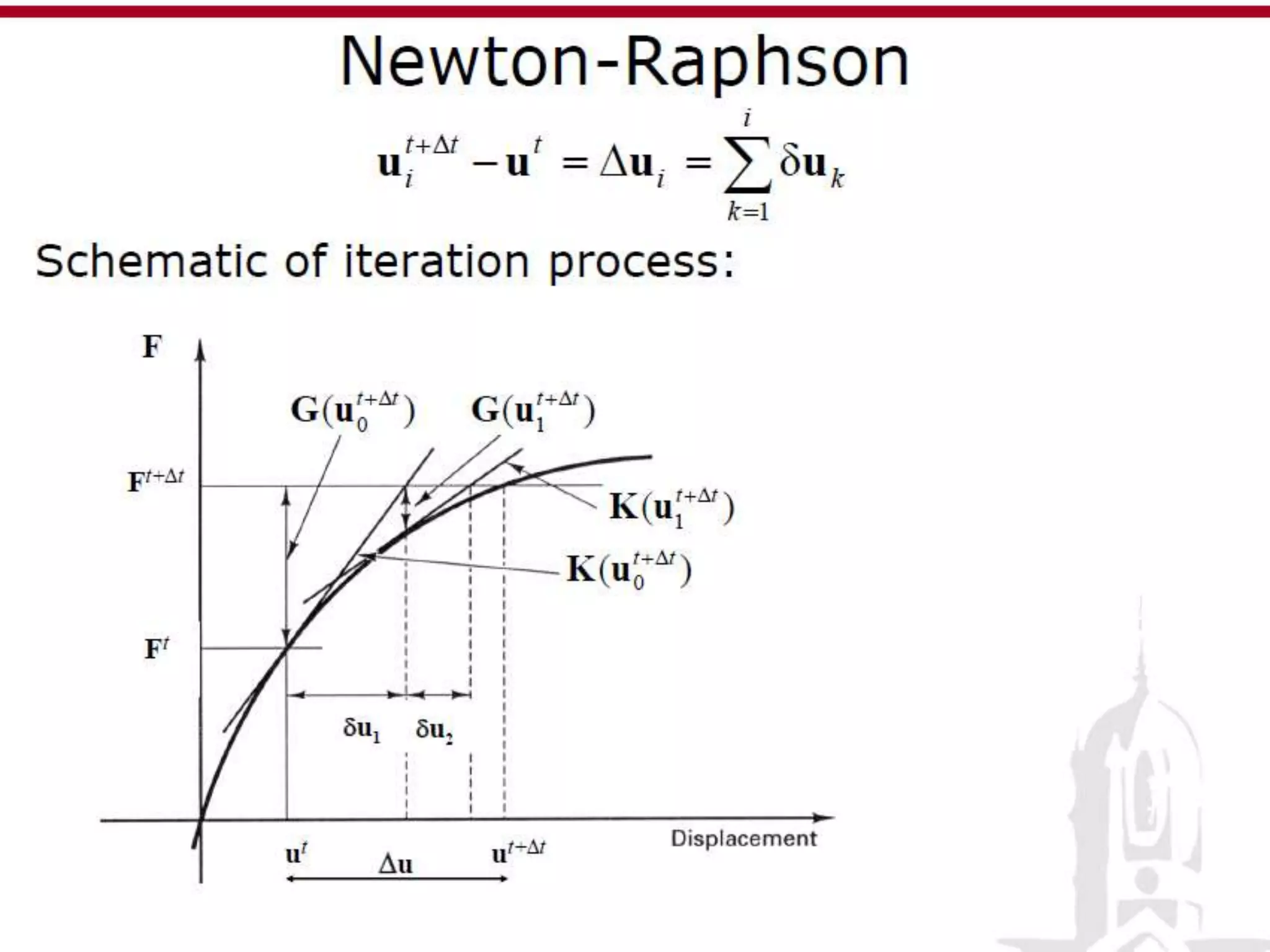
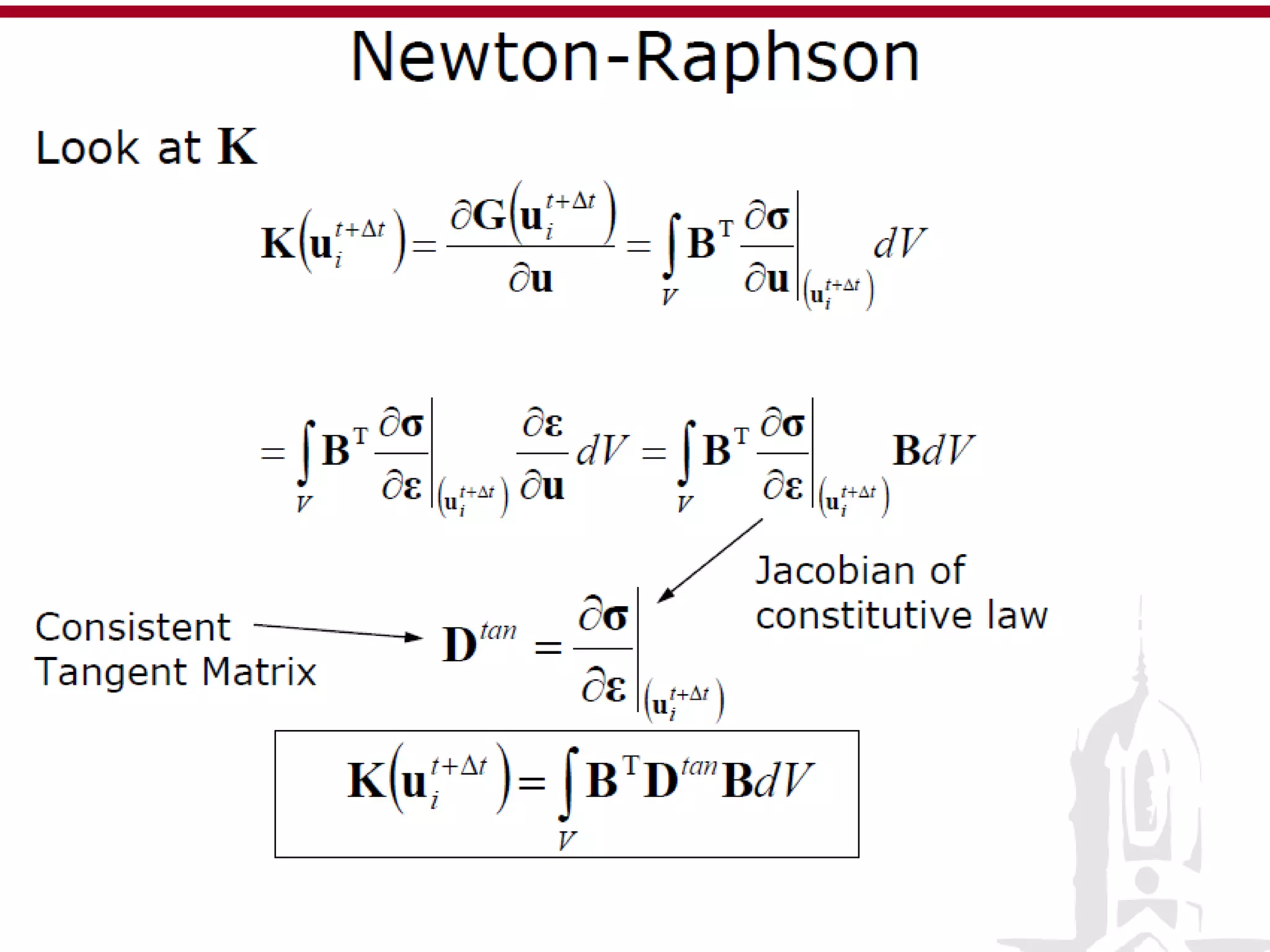
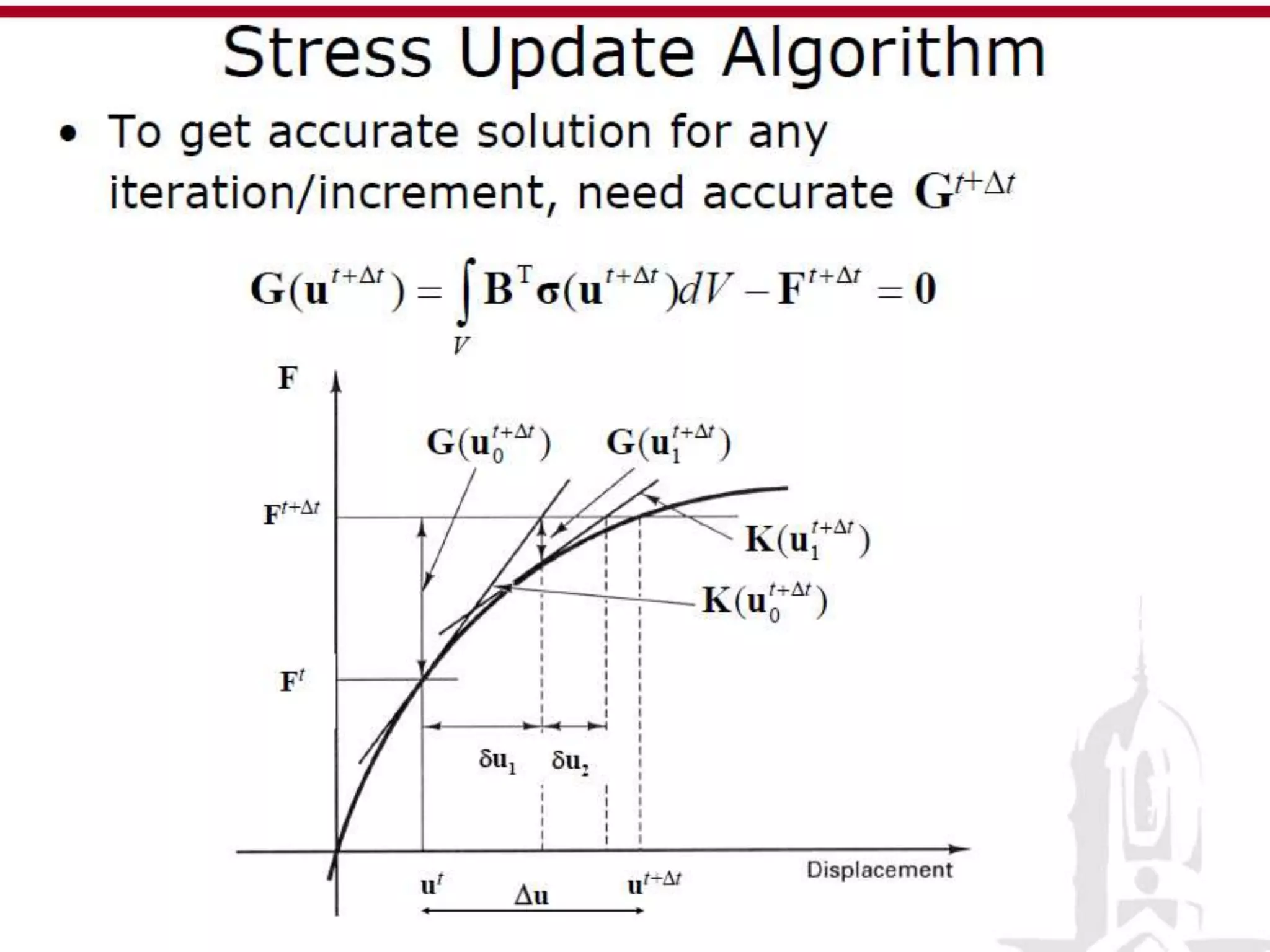
This document discusses finite element analysis and nonlinear finite element analysis. It introduces the finite element method and how it approximates solutions by dividing them into discrete elements. It explains that higher order polynomials and more nodes/elements increase accuracy. The document distinguishes between linear and nonlinear problems, with nonlinear problems not obeying Hooke's law. It lists common finite element methods for nonlinear mechanics like updated Lagrangian formulations. Finally, it discusses solution algorithms for nonlinear problems like Newton's method and line searches.

1. FEM(non
linear
analysis)
Unit-5
S. YUVARAJ
ASSISTANT PROFESSOR
K.S.R. COLLEGE OF ENGINEEING
TIRUCHENGODE

2. FEM(Finite Element Method)
• The finite element method is a means of
obtaining approximate numerical solutions to
field problems”.
• Replace solution variable distribution with
approximate distribution based on:
– fixed solution “shapes” over elements
– solution variable values at nodes
• Continuous → Discrete

4. FE Approximation
• Temperature distribution u(x)
– a single degree of freedom case
(SDOF)

5. • Approximation: assumption of “shape” of
solution throughout element – usually
polynomial – linear,quadratic,…
• More nodes & elements → greater accuracy
• Generally quadratic better than linear

12. Types of FEM problems
• Linear problems.(obeys hook’s law)
• Non linear problems.(hook’s law not
applicable)

15. Linear Graph

19. FE Methods of Nonlinear Mechanics (TB)
• Semidiscretization of Continuum Equations
• Static and Dynamic Discrete Equations
• Lagrangian, Eulerian, and Arbitrary Lagrangian
Eulerian (ALE) meshes
• Frame Invariant Stress Rates
• Total and Updated Lagrangian Formulations
• Material and Geometric Stiffness

20. Solution Algorithms for Nonlinear Problems
(TH)
• Newton and Modified Newton Methods
• Consistent Linearization
• Line Search
• Quasi-Newton Updates ("BFGS", etc.)
• Arc-Length Strategies

38. Information
• For other algorithms refer non-linear finite
element analysis by j.n reddy.