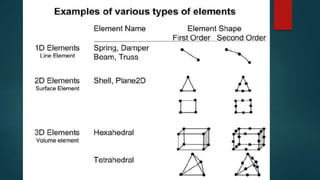
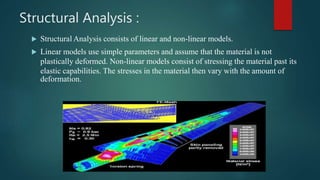
The document discusses the finite element method (FEM). FEM is a numerical technique used to find approximate solutions to partial differential equations. It divides a complex problem into small, simpler elements that are solved using relations between each other. There are three phases: pre-processing to mesh the geometry and apply properties/conditions, solution to derive equations and solve for quantities, and post-processing to validate solutions. FEM can model various problem types like static, dynamic, structural, vibrational, and heat transfer analyses. It has advantages like handling complex geometries and loadings but also disadvantages like requiring approximations and computational resources.

1. Finite Element
Method
DR HASSAN ALI
DEPARTMENT OF PHYSICS
UNIVERSITY OF NAROWAL

2. What is Finite Element Method?
 The Finite Element Method (FEM) is a numerical technique for
finding approximate solutions to boundary value problems for
partial differential equations.
 In simple terms, FEM is a method for dividing up a very complicated
problem into small elements that can be solved in relation to each
other.
 Useful for problems with complicated geometries, loadings, and
material properties where analytical solutions can not be obtained.

3. Boundary Value Problem
• A boundary value problem is a
differential equation together with a set
of additional constraints, called the
boundary conditions.
• A boundary value is a data value that
corresponds to a minimum or
maximum, input or output value
specified for a system or component.

4. Phases for FEM
 Pre–Processing:
 Here a finite element mesh is developed to divide the given geometry into
subdomains for mathematical analysis and the material properties are
applied and also the boundary conditions.
 Solution:
 In this phase governing matrix equations are derived and the solution for
the primary quantities is generated.
 Post-Processing:
 In the last phase, checking of the validity of the solution generated,
examination of the values of primary quantities such as displacement and
stresses, errors involved is carried out.

5. Types of FEM Element
 1-D Element
 2-D Element
 3-D Element
1-D Element:- if the displacement at each node of an element is
expressed in only one direction, then that element is called as 1-
D element.
Example:- Line Element, Bar Element

6.  2-D Element:- if the displacement at each node of an
element is expressed in two mutually perpendicular
directions, then that element is called as 2-D element.
 Example:- Triangular Element, Quadrilateral Element
 3-D Element:- if the displacement at each node of an
element is expressed in three mutually perpendicular
directions, then that element is called as 3-D element.
 Example:- Prism, Tetrahedron, Hexahedron

8. Static analysis is good for engineering, to find
just the end result.
Dynamic analysis is good for simulation, to
find all intermediate steps.
Static vs. Dynamic FEM

9. How Does Finite Element Analysis
Work?
FEA uses a complex system of points called nodes which make a grid called a mesh.
 This mesh is programmed to contain the material and structural properties which
define how the structure will react to certain loading conditions.
 Nodes are assigned at a certain density throughout the material depending on the
anticipated stress levels of a particular area.
 Regions which will receive large amounts of stress usually have a higher node density
than those that experience little or no stress. Points of interest may consist of:
fracture points of previously tested material, fillets, corners, complex detail, and high-
stress areas.
 The mesh acts like a spider web in that from each node, there extends a mesh
element to each of the adjacent nodes. This web of vectors is what carries the
material properties to the object, creating many elements.

10. Structural Analysis :
 Structural Analysis consists of linear and non-linear models.
 Linear models use simple parameters and assume that the material is not
plastically deformed. Non-linear models consist of stressing the material past its
elastic capabilities. The stresses in the material then vary with the amount of
deformation.

11. Vibrational Analysis :
 It is used to test a material against random vibrations, shock, and impact. Each of
these incidences may act on the natural vibrational frequency of the material
which, in turn, may cause resonance and subsequent failure.

12. Fatigue Analysis :
 Fatigue analysis helps designers to predict
the life of a material or structure by
showing the effects of cyclic loading on
the specimen.
 Such analysis can show the areas where
crack propagation is most likely to occur.
Failure due to fatigue may also show the
damage tolerance of the material.

13. Heat Transfer Analysis :
 Heat transfer analysis models the conductivity or thermal fluid dynamics of the
material or structure. This may consist of a steady state or transient transfer.
 Steady-state transfer refers to constant thermal properties in the material that
yields linear heat diffusion.

14. Applications of FEM
The FEM offers many important applications to the design engineer:
 Easily applied to complex, irregular-shaped objects composed of several different
materials and having complex boundary conditions.
 Applicable to steady-state, time-dependent and eigenvalue problems.
 Applicable to linear and nonlinear problems.
 One method can solve a wide variety of problems, including problems in solid
mechanics, fluid mechanics, chemical reactions, electromagnetics, biomechanics,
heat transfer and acoustics, to name a few.

15. Advantages Of FEM
 Can readily handle complex geometry.
 Can handle complex analysis types like vibration, heat transfer, fluids etc.
 Can handle complex loading:
 i. Node-based loading (point loads).
 ii. Element-based loading (pressure, thermal, inertial forces).
 iii. Time or frequency-dependent loading.
 Can handle complex restraints: Indeterminate structures can be analyzed.
 Can handle bodies comprised of nonhomogeneous materials: Can handle
bodies comprised of non-isotropic materials: Orthotropic & Anisotropic.
 Special material effects are handled such as temperature-dependent
properties, plasticity, creep, swelling etc.

16. Disadvantages Of FEA
 A specific numerical result is obtained for a specific problem.
 The FEM is applied to an approximation of the mathematical model of a system (the
source of so-called inherited errors).
 Experience and judgment are needed in order to construct a good finite element model.
 A powerful computer and reliable FEM software are essential.
 Input and output data may be large and tedious to prepare and interpret.
 Numerical errors such as the limitation of the number of significant digits, and rounding–
off occur very often.