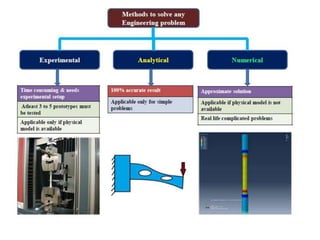
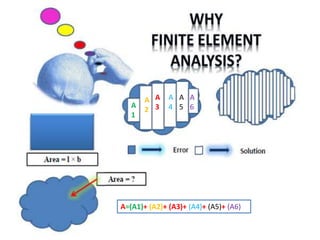
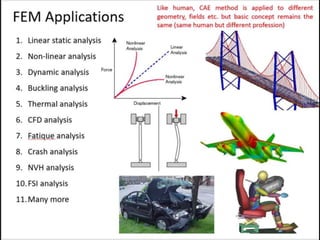
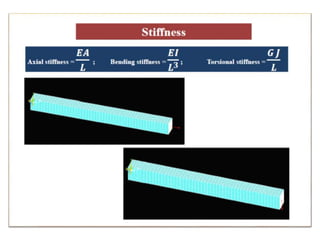
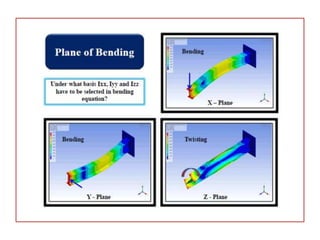
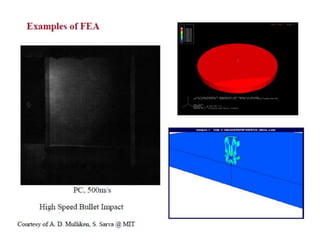
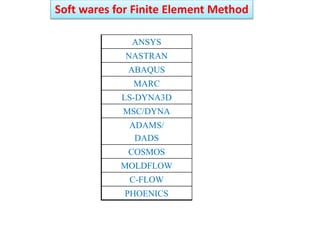
This document provides an overview of finite element analysis (FEA). It defines FEA as a numerical method for solving governing equations over the domain of a continuous physical system that is discretized into simple shapes. It lists several common structural and non-structural applications of FEA, such as stress analysis, buckling problems, vibration analysis, and heat transfer. Finally, it provides the course outline, textbooks, references, and some common FEA software packages.

1. 1
ME8692 FINITE ELEMENT ANALYSIS
DHIRAJLAL GANDHI COLLEGE OF
TECHNOLOGY
Dr.P.Parandaman, M.E., Ph.D.,
Associate Professor,
Department of Mechanical Engineering,
Dhirajlal Gandhi College of Technology,
Salem - 636309.

4. FEM is a numerical method for
solving a system of governing
equations over the domain of a
continuous physical system,
which is discretized into simple
geometric shapes called finite
element.

5. A
2
A
1
A
3
A
4
A
5
A
6
A=(A1)+ (A2)+ (A3)+ (A4)+ (A5)+ (A6)

6. Structural Problem Non-structural Problem
Stress Analysis
- truss & frame analysis
- stress concentrated
problem
Buckling problem
Vibration Analysis
Impact Problem
Heat Transfer
Fluid Mechanics
Electric or Magnetic
Potential
Applications of Finite Element Method

7. Structure analysis : a cantilever, a bridge, an oil platform…
Solid mechanics : a gear, a automotive power train …
Dynamics : vibration of Tower, earthquake, bullet
impact…
Thermal analysis : heat radiation of finned surface,
thermal stress brake disc…
Electrical analysis : Piezo actuator, electrical signal
propagation…
Biomaterials : human organs and tissues…

16. ME8692 FINITE ELEMENT ANALYSIS
UNIT I INTRODUCTION
Historical Background – Mathematical Modeling
of field problems in Engineering – Governing
Equations – Discrete and continuous models –
Boundary, Initial and Eigen Value problems–
Weighted Residual Methods – Variational
Formulation of Boundary Value Problems – Ritz
Technique – Basic concepts of the Finite Element
Method.

17. ME8692 FINITE ELEMENT ANALYSIS
UNIT II ONE-DIMENSIONAL PROBLEMS
One Dimensional Second Order Equations –
Discretization – Element types- Linear and Higher
order Elements – Derivation of Shape functions
and Stiffness matrices and force vectors-
Assembly of Matrices - Solution of problems from
solid mechanics and heat transfer. Longitudinal
vibration frequencies and mode shapes. Fourth
Order Beam Equation –Transverse deflections and
Natural frequencies of beams.

18. ME8692 FINITE ELEMENT ANALYSIS
UNIT III TWO DIMENSIONAL SCALAR VARIABLE
PROBLEMS
Second Order 2D Equations involving Scalar
Variable Functions – Variational formulation –
Finite Element formulation – Triangular elements
– Shape functions and element matrices and
vectors.
Application to Field Problems - Thermal problems
– Torsion of Non circular shafts –Quadrilateral
elements – Higher Order Elements.

19. ME8692 FINITE ELEMENT ANALYSIS
UNIT IV TWO DIMENSIONAL VECTOR
VARIABLE PROBLEMS
Equations of elasticity – Plane stress, plane strain
and axisymmetric problems – Body forces and
temperature effects – Stress calculations - Plate
and shell elements.

20. ME8692 FINITE ELEMENT ANALYSIS
UNIT V ISOPARAMETRIC FORMULATION
Natural co-ordinate systems – Isoparametric
elements – Shape functions for iso parametric
elements – One and two dimensions –
Serendipity elements – Numerical integration and
application to plane stress problems - Matrix
solution techniques – Solutions Techniques to
Dynamic problems – Introduction to Analysis
Software.

21. ME8692 FINITE ELEMENT ANALYSIS
TEXT BOOKS:
1. Reddy. J.N., “An Introduction to the Finite
Element Method”, 3rd Edition, Tata McGraw-Hill,
2005
2. Seshu, P, “Text Book of Finite Element Analysis”,
Prentice-Hall of India Pvt. Ltd., New Delhi,
2007.

22. ME8692 FINITE ELEMENT ANALYSIS
REFERENCES:
1. Bhatti Asghar M, "Fundamental Finite Element Analysis and
Applications", John Wiley & Sons, 2005 (Indian Reprint 2013)*
2. Chandrupatla & Belagundu, “Introduction to Finite Elements in
Engineering”, 3rd Edition, Prentice Hall College Div, 1990
3. Logan, D.L., “A first course in Finite Element Method”, Thomson Asia
Pvt. Ltd., 2002
4. Rao, S.S., “The Finite Element Method in Engineering”, 3rd Edition,
Butterworth Heinemann, 2004
5. Robert D. Cook, David S. Malkus, Michael E. Plesha, Robert J.
Witt, “Concepts and Applications of Finite Element Analysis”, 4th
Edition, Wiley Student Edition, 2002.

23. ANSYS
NASTRAN
ABAQUS
MARC
LS-DYNA3D
MSC/DYNA
ADAMS/
DADS
COSMOS
MOLDFLOW
C-FLOW
PHOENICS
Soft wares for Finite Element Method