Quicksort is a divide and conquer algorithm that works by partitioning an array around a pivot value and recursively sorting the subarrays. It first selects a pivot element and partitions the array by moving all elements less than the pivot before it and greater elements after it. The subarrays are then recursively sorted through this process. When implemented efficiently with an in-place partition, quicksort is one of the fastest sorting algorithms in practice, with average case performance of O(n log n) time but worst case of O(n^2) time.

1. Quick Sort
Afaq Mansoor Khan
BSSE 2017-21
IMSciences Peshawar

2. What is Quick Sort?
• Quick sort is a divide and conquer algorithm
which relies on a partition operation:
– to partition an array an element called a pivot is
selected
• All elements smaller than the pivot are moved
before it and all greater elements are moved
after it
• The lesser and greater sublists are then
recursively sorted
2

3. Quick sort
• Efficient implementations (with in-place
partitioning), somewhat complex, but are
among the fastest sorting algorithms in
practice
• One of the most popular sorting algorithms
and is available in many standard
programming libraries.

4. Idea of Quick-Sort
1) Divide : If the sequence S has 2 or more elements,
select an element x from S to be your pivot. Any
arbitrary element, like the last, will do. Remove all the
elements of S and divide them into 3 sequences:
L, holds S’s elements less than x
E, holds S’s elements equal to x
G, holds S’s elements greater than x
2) Recurse: Recursively sort L and G
3) Conquer: Finally, to put elements back into S in order,
first inserts the elements of L, then those of E, and
those of G.

5. Idea of Quick Sort
1) Select: pick an element
2) Divide: rearrange elements so
that x goes to its final position E
3) Recurse and Conquer:
recursively sort

6. Two key steps
• How to pick a pivot?
• How to partition?

7. Pick a pivot
• Use the first element as pivot
– if the input is random, ok
– if the input is presorted (or in reverse order)
• all the elements go into S2 (or S1)
• Results in O(n2) behavior (Analyze this case later)
• Choose the pivot randomly
– generally safe

8. A better partition
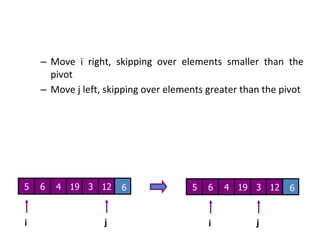
• Want to partition an array A[left .. right]
• First, get the pivot element out of the way by swapping it with the last
element. (Swap pivot and A[right])
pivot i j
5 6 4 6 3 12 19 5 6 4 63 1219
swap

9. – Move i right, skipping over elements smaller than the
pivot
– Move j left, skipping over elements greater than the pivot
i j
5 6 4 63 1219
i j
5 6 4 63 1219

10. • When i and j have stopped and i is to the left of j
– Swap A[i] and A[j]
• The large element is pushed to the right and the small element is pushed to
the left
– Repeat the process until i and j cross
swap
i j
5 6 4 63 1219
i j
5 3 4 66 1219

11. • When i and j have crossed
– Swap A[i] and pivot
• Result:
– A[x] <= pivot, for x < i
– A[x] >= pivot, for x > i
i j
5 3 4 66 1219
ij
5 3 4 66 1219
ij
5 3 4 6 6 12 19

12. Quicksort example
1
3
8
1
9
2
4
3
3
1
6
5
5
7
2
6
7
5
0
1
3
8
1
9
2
4
3
3
1
6
5
5
7
2
6
7
5
0
1
3 4
3
3
1
5
72
6
0
8
1
9
2
7
5
6
5
1
3
4
3
3
1
5
7
2
6
0
8
1
9
2
7
5
1
3
4
3
3
1
5
7
2
6
0
6
5
8
1
9
2
7
5
Select pivot
partition
Recursive call Recursive call
Merge

13. Quicksort Algorithm
• To sort a[left...right]:
1. if left < right:
1.1. Partition a[left...right] such that:
all a[left...p-1] are less than a[p], and
all a[p+1...right] are >= a[p]
1.2. Quicksort a[left...p-1]
1.3. Quicksort a[p+1...right]
2. Terminate

14. Quick Sort Source Code C++
void QuickSort(int list[], int left, int right) {
int pivot, leftArrow, rightArrow;
leftArrow = left;
rightArrow = right;
pivot = list[(left + right) / 2];
do {
while (list[rightArrow] > pivot)
rightArrow--;
while (list[leftArrow] < pivot)
leftArrow++;
if (leftArrow <= rightArrow) {
Swap_Data(list[leftArrow], list[rightArrow]);
leftArrow++;
rightArrow--;
}
}
while (rightArrow >= leftArrow);
if (left < rightArrow)
QuickSort(list, left, rightArrow);
if (leftArrow < right)
QuickSort(list, leftArrow, right);
}

15. Quick Sort Pseudo Code
• QuickSort(A,start,end)
• { if(start<end)
• { pIndex 🡨 partition(A,start,end)
QuickSort(A,start,Pindex-1)
QuickSort(A,Pindex+1,end)
}
}
• Partition(A,start,end)
• { pivot 🡨 A[end]
Pindex 🡨 start
For i 🡨 start to end-1
{
If(A[i] <= pivot)
{ Swap(a[i],P[pindex])
Pindex 🡨 Pindex+1
}
}
Swap(A[pindex] , A[end])
Return Pindex }

16. Complexity of Quick Sort
• Best case performance O(n log n)
• Average case performance O(n log n)
• Worst case performance O(n2)
• Worst case space complexity auxiliary O(log n)
• Where n is the number of elements to be sorted

17. Questions?

18. THANK YOU!
☺

19. References
• Data Structures and Algorithm Analysis by M. A.
Weiss, 2nd edition
• https://cs.nyu.edu/courses/spring99/V22.0102-
002/quick.html
• www.dcs.gla.ac.uk/~pat/52233/slides/QuickSort1x1.
pdf