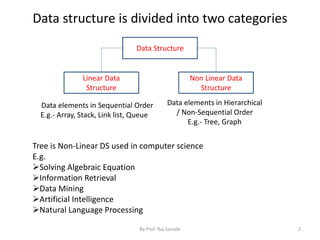
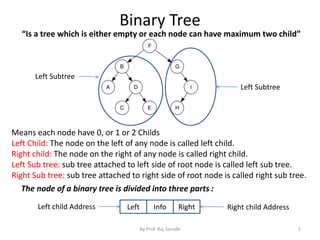
Chapter 6 discusses tree data structures, categorizing them into linear and non-linear structures, with a focus on trees, which are used in various computer science applications. The chapter covers tree terminology, classifications of binary trees, and representation methods like sequential and linked representations. Additionally, it explains binary search trees and their operations, including construction and traversal methods.

1. Chapter 6
Tree

2. Data structure is divided into two categories
By Prof. Raj Sarode 2
Linear Data
Structure
Non Linear Data
Structure
Data Structure
Data elements in Sequential Order
E.g.- Array, Stack, Link list, Queue
Data elements in Hierarchical
/ Non-Sequential Order
E.g.- Tree, Graph
Tree is Non-Linear DS used in computer science
E.g.
Solving Algebraic Equation
Information Retrieval
Data Mining
Artificial Intelligence
Natural Language Processing

3. Tree
“Tree is a finite collection of special Data items
called the NODE ”
The node of Tree are arranged in the
hierarchical structure to represent the parent-child
relationship.
 First node of tree does not have any parent is
called the Root (node) of tree.
Parent is connected through an edge to its
child or descendents.
By Prof. Raj Sarode 3

4. By Prof. Raj Sarode 4
Tree Terminology :-
Node
Root
Edge
1. Node: Each Elements of Tree is called node
2. Edges: The Lines Connecting the nodes are called Edges.
3. Parent Node: The Immediate predecessor of node is called parent node.
4. Grand Parent: Parent of Parent
5. Child Node: All the immediate successor of a node are its child node.
6. Root Node: The node does not having any parent.
7. Leaf Node: The node does not having any child called Leaf node or Terminal node.
8. Level: Level of Node is distance of that node from root.
(Rot node at distance 0 from itself hence is at level 0)
9. Height: Total No. of level in tree (is equal to depth of tree)
10. Degree of Node: No. of children it has.
11. Siblings: children of the same parent node (two or more node have same parent are
called sibling or brother

5. Binary Tree
“Is a tree which is either empty or each node can have maximum two child”
Means each node have 0, or 1 or 2 Childs
Left Child: The node on the left of any node is called left child.
Right child: The node on the right of any node is called right child.
Left Sub tree: sub tree attached to left side of root node is called left sub tree.
Right Sub tree: sub tree attached to right side of root node is called right sub tree.
By Prof. Raj Sarode 5
Left Subtree
Left Subtree
The node of a binary tree is divided into three parts :
Left child Address Left Info Right Right child Address

6. Classification of Binary Tree
By Prof. Raj Sarode 6
1. Strictly Binary Tree:
Each node in a tree is either Leaf or has exactly two children
Strictly binary tree with n Leaves always contains 2n-1 nodes
E.g.
2 Leaves in First Example having 2*2-1=3 Nodes.
3 Leaves in Second Example having 3*2-1=5 Nodes.
4 Leaves in Third Example having 4*2-1=7 Nodes

7. Classification of Binary Tree
By Prof. Raj Sarode 7
2. Complete Binary Tree:
A binary tree where having height h is a strictly binary tree and all
leaves are at h levels that tree is complete binary tree
Or
All the terminal node of a tree are at level d ,where d is the depth of
tree, then such trees are called complete binary tree.

8. Classification of Binary Tree
3. Almost Complete Binary Tree:
A binary tree in which all the terminal node or leaf node of tree are at
level d or d-1, where d is the depth of tree, then such trees are
called almost complete binary tree.
L 0
L 1
L 2
L 3
By Prof. Raj Sarode 8
L 0
L 1
L 2

9. Classification of Binary Tree
By Prof. Raj Sarode 9
4. Extended Binary Tree:
If in a binary tree ,each empty sub tree (Leaf Node) is replaced by a
special node then the resulting tree is extended binary tree or 2-tree
 We can add special node to leaf node & node that have only one child.
 The special nodes added to the tree are called External Node & original
node of tree are called Internal Node
External Node
Internal Node
Binary Tree
Extended Binary Tree
Note: Binary Tree of Height h has maximum (2 h+1 - 1) nodes

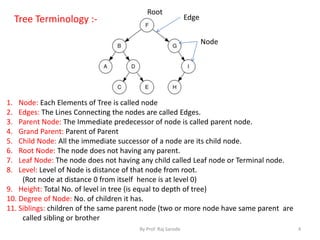
10. Representation of Tree
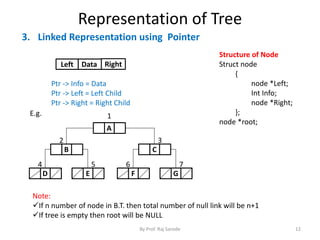
1. Sequential Representation using array
 Tree is store in single array
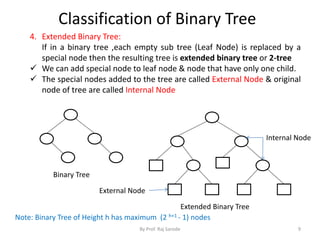
 Number are assigned to each node from leftmost to rightmost node.
 Root node always assign no. 1
 Left Child is placed at position [2 * K] (k is position of root)
 Right Child is placed at position [2 * K + 1]
 Size of array is Depends on Depth of tree i.e. 2 d+1
By Prof. Raj Sarode 10
A
B C
D E F G
H I
1
2 3
4 5 6 7
8 9
Root (A) =1
L Child = [2*k]= 2 * 1 =2 (B)
R child = [2 * K + 1] = 2 * 1 + 1 = 3 (C)
Root(B)=2
L Child = [2*k]= 2 * 2 =4 (D)
R child = [2 * K + 1] = 2 * 2 + 1 = 5 (E)
Note: If root is placed at 0th position then
L Child = [2 * k + 1 ]
R child = [2 * K + 2 ]

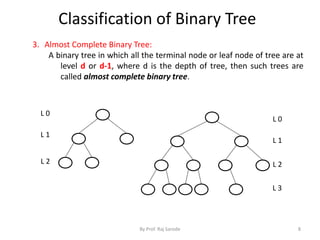
11. Representation of Tree
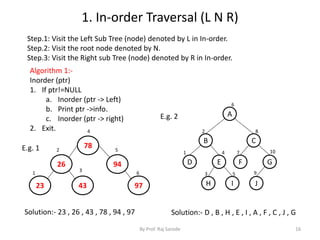
2. Linked Representation using array
 Tree is store in single array
Structure of Node
Struct mode
{
Int Left;
Int Info;
Int Right;
};
Node Tree[10];
1
2 3
B C
6 7
By Prof. Raj Sarode 11
A
4 5
D E
Tree [ 1] . Info = A
Tree [ 1 ] . Left = 2
Tree [ 1 ] . Right = 3
F G
2 A 3
E.g.

12. Representation of Tree
3. Linked Representation using Pointer
Structure of Node
Struct node
{
node *Left;
Int Info;
node *Right;
};
node *root;
2 3
6 7
By Prof. Raj Sarode 12
Ptr -> Info = Data
Ptr -> Left = Left Child
Ptr -> Right = Right Child
1
A
B C
4 5
D E
F G
Left Data Right
E.g.
Note:
If n number of node in B.T. then total number of null link will be n+1
If tree is empty then root will be NULL

13. Binary Search Tree
A binary Search Tree is special kind if tree that satisfied
the following conditions.
1. The data elements of left sub tree are smaller than
the root of the tree.
2. The data elements of right sub tree are greater than
or equal to the root of the tree.
3. The left sub tree and right sub tree are also the
binary search trees, i.e. they must also follow the
above two rules.
By Prof. Raj Sarode 13

14. Operation on Binary Search Tree
1. Construction of binary Search Tree (BST)
Step.1: Initially tree is empty ,place the first element at the root.
Step.2: Compare the next element with root
if element is grater than or equal to root then place it in right child position.
else
place it in the left child position.
Step.3: Repeat the process (step 2) for the next element until end of elements or nodes.
E.g. 30, 26, 35, 9, 12, 19, 32, 40, 50, 45, 2, 9
30
26 35
9 12 32 40
2 9 19 45 50
By Prof. Raj Sarode 14

15. Operation on Binary Search Tree
2. Traversal of binary Search Tree
it is the process in which each node of tree is visited exactly once
Step.1: Visit the root node denoted by N.
Step.2: Visit the Left Sub Tree (node) denoted by L.
Step.3: Visit the Right sub Tree (node) denoted by R.
Methods of Traversal
1.In-order Traversal
2.Pre-order Traversal
3.Post-order Traversal
By Prof. Raj Sarode 15

16. 1. In-order Traversal (L N R)
Step.1: Visit the Left Sub Tree (node) denoted by L in In-order.
Step.2: Visit the root node denoted by N.
Step.3: Visit the Right sub Tree (node) denoted by R in In-order.
Algorithm 1:-
Inorder (ptr)
1. If ptr!=NULL
6
By Prof. Raj Sarode 16
a. Inorder (ptr -> Left)
b. Print ptr ->info.
c. Inorder (ptr -> right)
2. Exit.
78
26 94
23 43 97
Solution:- 23 , 26 , 43 , 78 , 94 , 97
A
B C
D E F G
H I J
Solution:- D , B , H , E , I , A , F , C , J , G
E.g. 1
E.g. 2
1
2
3
4
5
6
1
2
3
4
5
7
8
9
10

17. 2. Pre-order Traversal (N L R)
Step.1: Visit the root node denoted by N.
Step.2: Visit the Left Sub Tree (node) denoted by L in Pre-order.
Step.3: Visit the Right sub Tree (node) denoted by R in Pre-order.
Algorithm 2:-
Preorder (ptr)
1. If ptr!=NULL
By Prof. Raj Sarode 17
a. Print ptr ->info.
b. Preorder (ptr -> Left)
c. Preorder (ptr -> right)
2. Exit.
78
26 94
23 43 97
Solution:- 78 , 26 , 23 , 43 , 94 , 97
A
B C
D E F G
H I J
Solution:- A , B , D , E , H , I , C , F , G , J
E.g. 1
E.g. 2
1
2
3 4
5
6
1
2
3 4
5 6
7
8 9
10

18. 3. Post-order Traversal (L R N)
Step.1: Visit the Left Sub Tree (node) denoted by L in Post-order.
Step.2: Visit the Right sub Tree (node) denoted by R in Post-order.
Step.3: Visit the root node denoted by N.
Algorithm 3:-
Postorder (ptr)
1. If ptr !=NULL
4
5
By Prof. Raj Sarode 18
a. Postorder (ptr -> Left)
b. Postorder (ptr -> right)
c. Print ptr ->info.
2. Exit.
78
3
26 94
23 43 97
Solution:- 23 , 43 , 26 , 97 , 94 , 78
A
B C
D E F G
H I J
Solution:- D , H , I , E , B , F , J , G , C , A
E.g. 1
E.g. 2
1 2
4
5
6
1
2 3
6
7
8
9
10

19. Thank You
By Prof. Raj Sarode 19