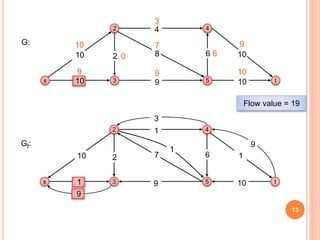
The document summarizes the Ford-Fulkerson algorithm for finding the maximum flow in a flow network. It defines key terms like flow network, source, sink, flow, residual graph and augmented path. It then outlines the steps of the Ford-Fulkerson algorithm to incrementally send flow along augmented paths from the source to the sink until no more such paths exist. An example applying the algorithm to find the maximum flow in a sample network is provided with illustrations of the residual capacities after each flow augmentation.

1. FORD FULKERSON
ALGORITHM
Adarsh V R
ME Scholar, UVCE
K R Circle, Bangalore

2.  Flow network is a directed graph G=(V,E) such that each
edge has a non-negative capacity c(u,v)≥0.
 Two distinguished vertices exist in G namely :
• Source (denoted by s) : In-degree of this vertex is 0.
• Sink (denoted by t) : Out-degree of this vertex is 0.
 Flow in a network is an integer-valued function f defined on
the edges of G satisfying 0 ≤ f(u,v) ≤ c(u,v), for every
Edge(u,v) in E.
 Augmented Path is a path from source s to sink t in a
residual graph.
 Residual Graph is graph after sending the flow through the
network with edges having remaining capacities (residual
capacity).
2

3. • FORD-FULKERSON(G,s,t)
• for each edge (u,v)  E[G]
• do f[u,v] 0
• f[v,u] 0
• while there exists a path p from s to t in the residual
network Gf
• do cf(p) min{cf(u,v): (u,v) is in p}
• for each edge (u,v) in p
• do f[u,v] f[u,v]+cf(p) 3




Ford Fulkerson Algorithm

4.  After every step in the algorithm the following is
maintained:
• Capacity Constraints : ∀ 𝑢, 𝑣 𝜖 𝐸 𝑓 𝑢, 𝑣 ≤ 𝑐(𝑢, 𝑣)
 The flow along an edge can not exceed its capacity.
• Skew Symmetry : ∀ 𝑢, 𝑣 𝜖 𝐸 𝑓 𝑢, 𝑣 = −𝑓(𝑣, 𝑢)
 The net flow from u to v must be the opposite of the net flow from v to u
• Flow Conservation :
 Unless u is s or t. The net flow to a node is zero, except for the source, which
"produces" flow, and the sink, which "consumes" flow.
4

5. When the algorithm terminates?
All paths from s to t are blocked by either a
• Full forward edge
• Empty backward edge
5

6. EXAMPLE:
s
2
3
4
5 t10
10
9
8
4
10
1062
0
0
0
0 0 0
0
0
G:
Flow value = 0
0
flow
capacity
6

7. s
2
3
4
5 t10
10
9
8
4
10
1062
0
0
0
0 0 0
0
0
G:
s
2
3
4
5 t10 9
4
1062
Gf:
10 8
10
8 8
8
X X
X
0
Flow value = 0
capacity
residual capacity
flow
7

8. s
2
3
4
5 t10
10
9
8
4
10
1062
8
0
0
0 0 8
8
0 0
G:
s
2
3
4
5 t10
4
106
Gf:
8
8
8
9
22
2
10
2
10
X
X
X2X
Flow value = 8
8

9. 0
s
2
3
4
5 t10
10
9
8
4
10
1062
10
0
0
0 2 10
8
2
G:
s
2
3
4
5 t
4
2
Gf:
10
810
2
10 7
106
X
6
6
6
X
X
8X
Flow value = 10
9

10. s
2
3
4
5 t10
10
9
8
4
10
1062
10
0
6
6 8 10
8
2
G:
s
2
3
4
5 t1
6
Gf:
10
810
8
6
6
6
4
4
4
2
X
8
2
8
X
X
0
X
Flow value = 16
10

11. s
2
3
4
5 t10
10
9
8
4
10
1062
10
2
8
8 8 10
8
0
G:
s
2
3
4
5 t
62
Gf:
10
10
8
6
8
8
2
2 1
2
8 2
X
9
7 9
X
X
9X
X 3
Flow value = 18
11

12. s
2
3
4
5 t10
10
9
8
4
10
1062
10
3
9
9 9 10
7
0
G:
s
2
3
4
5 t1 9
1
162
Gf:
10
710
6
9
9
3
1
Flow value = 19
12

13. s
2
3
4
5 t10
10
9
8
4
10
1062
10
3
9
9 9 10
7
0
G:
s
2
3
4
5 t1 9
1
162
Gf:
10
710
6
9
9
3
1
Flow value = 19
13

14. 14