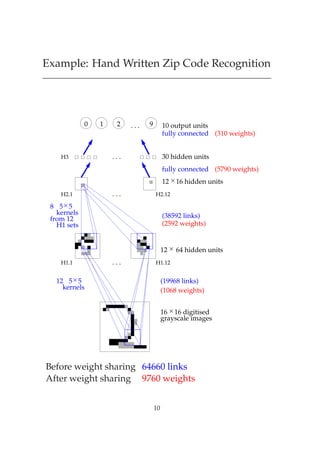
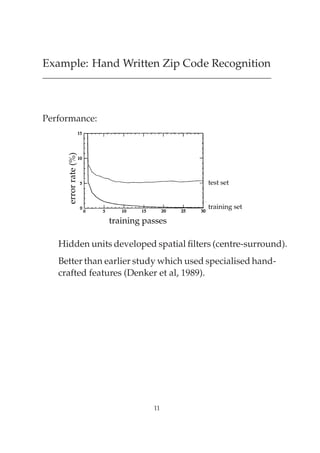
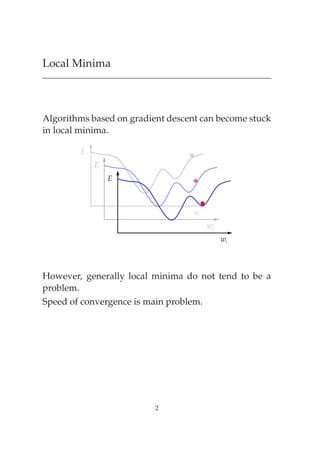
The document discusses the back propagation learning algorithm. It can be slow to train networks with many layers as error signals get smaller with each layer. Momentum and higher-order techniques can speed up learning. Examples are given of applying back propagation to tasks like speech recognition, encoding/decoding patterns, and handwritten digit recognition. While popular, back propagation has limitations like potential local minima issues and lack of biological plausibility in its error backpropagation process.

1. The Back Propagation Learning Algorithm
BP is extensively used and studied.
Local minima.
Learning can be slow.
Practical examples.
Handling time.
1

2. Local Minima
Algorithms based on gradient descent can become stuck
in local minima.
E
E
E
wi
wi
wi
However, generally local minima do not tend to be a
problem.
Speed of convergence is main problem.
2

3. Learning can be Slow
The more layers the slower learning becomes:
¡
¡Û Ý Ø ßÞ ´½ Ý µ Ú
Ý
Æ
¡Ù Æ Û Ú ´½ Ú µ Ü
ßÞ
Æ
.
.
.
Each error term Æ modifies the previous by a Ý ´½ Ý µ like
term.
Since Ý is a sigmoidal function (¼ Ý ½), then
¼ Ý´½ ݵ ¼ ¾
The more layers, the smaller the effective errors get, the
slower the network learns.
3

4. Speeding up Learning
A simple method to speeding up the learning is to add a
momentum term.
¡Û ´Ø · ½µ Û · « ¡Û ´Øµ
where ¼ « ½.
Each weight is given some “inertia” or “momentum” so
it tends to change in the direction of its average.
When weight change is same every iteration (e.g. when
travelling over plateau):
¡Û ´Ø · ½µ ¡Û ´Øµ
´½ «µ¡Û ´Ø · ½µ Û
¡Û ´Ø · ½µ ½ « Û
So, if « ¼ , effective learning rate is ½¼ .
Higher-order techniques (e.g. conjugate gradient) faster.
4

5. Encoder networks
Momentum = 0.9 Learning Rate = 0.25
Error
10.0
0.0
0 402
Input Set[3] Output Set[0]
Pat 1 Pat 1
Pat 2 Pat 2
Pat 3 Pat 3
Pat 4 Pat 4
Pat 5 Pat 5
Pat 6 Pat 6
Pat 7 Pat 7
Pat 8 Pat 8
8 inputs: local encoding, 1 of 8 active.
Task: reproduce input at output layer (“bottleneck”)
After 400 epochs, activation of hidden units:
Pattern Hidden units Pattern Hidden units
1 1 1 1 5 1 0 0
2 0 0 0 6 0 0 1
3 1 1 0 7 0 1 0
4 1 0 1 8 0 1 1
Also called “self-supervised” networks.
Related to PCA (a statistical method).
Application: compression.
Local vs distributed representations.
5

6. Example: NetTalk
Sejnowski, T. & Rosenberg, C. (1986). Parallel networks that learn
to pronounce English text. Complex Systems 1, 145–168.
task: to convert continuous text into speech.
input: a window of letters from English text drawn from
a 1000 word dictionary.
7-letter context to disambiguate “brave”, “gave” vs “have”
output: phonetic representation of speech (which can be
fed into a synthesiser).
s
Hidden Units
T h i s i s t h e i n p u t
6

7. Example: NetTalk
s 26 output units
80 hidden units
Hidden Units in a single layer
7 29 input units
¯ Input: letter encoded using 1 of 29 units (26 + 3 for
punctuation)
¯ Output: distributed representation across 21 features
including vowel height, position in mouth; 5 fea-
tures for stress.
Performance:
90% correct on training set.
80–87% correct on test set.
Two small hidden layers better than one big layer.
Babbling during learning?
Hidden representations: vowel v consonants?
7

8. Example: Hand Written Zip Code Recognition
LeCun, Y., Boser, B., Denker, J., Henderson, D., Howard, R., Hub-
bard, L. & Jackel, L. (1989). Backpropagation applied to hand-
written zip code recognition. Neural Computation 1, 541–551.
task: Network is to learn to recognise handwritten digits
taken from U.S. Mail.
input: Digitised hand written numbers.
output: One of 10 units is to be most active – the unit
that represents the correctly recognised numeral.
8

9. Example: Hand Written Zip Code Recognition
Real input (normalised digits from the testing set)
Knowledge of task constrains architecture.
“Feature detectors” useful.
Implemented by weight-sharing.
Reduces free parameters, speeds up learning.
9

10. Example: Hand Written Zip Code Recognition
0 1 2 ... 9 10 output units
fully connected (310 weights)
H3 ... 30 hidden units
fully connected (5790 weights)
12 16 hidden units
H2.1 ... H2.12
8 5 5
kernels (38592 links)
from 12
H1 sets (2592 weights)
12 64 hidden units
H1.1 ... H1.12
12 5 5 (19968 links)
kernels (1068 weights)
16 16 digitised
grayscale images
Before weight sharing 64660 links
After weight sharing 9760 weights
10

11. Example: Hand Written Zip Code Recognition
Performance:
error rate (%)
test set
training set
training passes
Hidden units developed spatial filters (centre-surround).
Better than earlier study which used specialised hand-
crafted features (Denker et al, 1989).
11

12. Handling temporal sequences
“Spatialise” time (e.g. NetTalk)
Add context units with fixed connections; some trace
over time.
Standard b.p. can be used in these cases.
(fig 7.5 of HKP)
For fully recurrent networks, b.p. extended to Real-
Time Recurrent Learning (Williams & Zipser, 1989).
12

13. Summary
Back propagation is popular training method.
Hidden units find useful internal representations.
Extendable to temporal sequences.
Problems: can be slow, no convergence theorem. Need
to try different architectures (#layers) , learning rates.
Biological plausibility?
1. Who provides the targets?
2. Can signals (errors) backpropagate from one cell
to another?
13