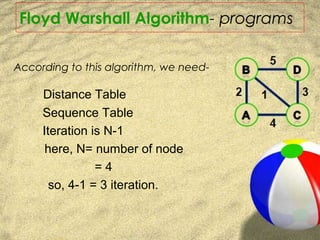
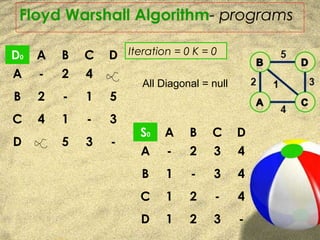
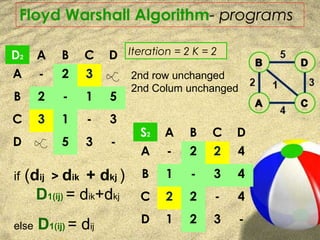
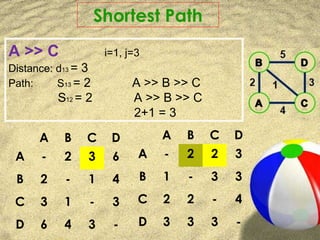
This document presents an overview of the Floyd-Warshall algorithm. It begins with an introduction to the algorithm, explaining that it finds shortest paths in a weighted graph with positive or negative edge weights. It then discusses the history and naming of the algorithm, attributed to researchers in the 1950s and 1960s. The document proceeds to provide an example of how the algorithm works, showing the distance and sequence tables that are updated over multiple iterations to find shortest paths between all pairs of vertices. It concludes with discussing the time and space complexity, applications, and references.

1. WELCOME
TO My
SESSION
Presented By:
MD. Saidur Rahman Kohinoor
DIU Student
E-mail: saidur95@gmail.com
Social Network: www.fb.com/kohinoor11

2. Presentation Topic:
Floyd Warshall’s
Algorithm

3. Floyd Warshall Algorithm - what?
An example of dynamic programming
An algorithm for finding shortest paths in
a weighted graph with positive or negative
edge weights
no negative cycles
find the lengths of the shortest paths
between all pairs of vertices

4. History and naming - how?
Bernard Roy in 1959
Robert Floyd in 1962
Stephen Warshall in 1962
Peter Ingerman in 1962

5. The algorithm is also known as
History and naming - how?
The Floyd's algorithm
 the Roy–Warshall algorithm
 the Roy–Floyd algorithm, or
 the WFI algorithm
The Floyd's algorithm
 the Roy–Warshall algorithm
 the Roy–Floyd algorithm, or
 the WFI algorithm

6. Shortest paths – mean?
Path 1: A -> B -> D = 7
Path 2: A -> C -> D = 7
Path 3: A -> B -> C -> D = 6
There are several paths
between A and D:
5
4
312

7. There are several things to notice here:
There can be more then one route
between two nodes.
The number of nodes in the route isn’t
important (Path 3 has 4 nodes but is
shorter than Path 1 or 2, which
has 3 nodes).
There can be more than one path of
minimal length.
Shortest paths – mean?

8. Floyd Warshall Algorithm- programs
Distance Table
Sequence Table
Iteration is N-1
here, N= number of node
= 4
so, 4-1 = 3 iteration.
According to this algorithm, we need-

9. Distance Table by D0, D1, D2, ……. ,Dn
Sequence Table by S0, S1, S2,……. ,Sn
Iteration by K
Here we denoted-
Floyd Warshall Algorithm- programs

10. D0 A B C D
A - 2 4
B 2 - 1 5
C 4 1 - 3
D 5 3 -
S0 A B C D
A - 2 3 4
B 1 - 3 4
C 1 2 - 4
D 1 2 3 -
Iteration = 0 K = 0
All Diagonal = null
Floyd Warshall Algorithm- programs

11. D1 A B C D
A - 2 4
B 2 - 1 5
C 4 1 - 3
D 5 3 -
S1 A B C D
A - 2 3 4
B 1 - 3 4
C 1 2 - 4
D 1 2 3 -
1st row unchanged
1st Colum unchanged
Iteration = 1 K = 1
if (dij > dik + dkj )
D1(ij) = dik+dkj
else D1(ij) = dij
Floyd Warshall Algorithm- programs

12. D2 A B C D
A - 2 3
B 2 - 1 5
C 3 1 - 3
D 5 3 -
S2 A B C D
A - 2 2 4
B 1 - 3 4
C 2 2 - 4
D 1 2 3 -
Iteration = 2 K = 2
2nd row unchanged
2nd Colum unchanged
if (dij > dik + dkj )
D1(ij) = dik+dkj
else D1(ij) = dij
Floyd Warshall Algorithm- programs

13. D3 A B C D
A - 2 3 6
B 2 - 1 4
C 3 1 - 3
D 6 4 3 -
S3 A B C D
A - 2 2 3
B 1 - 3 3
C 2 2 - 4
D 3 3 3 -
Iteration = 3 K = 3
3rd row unchanged
3rd Colum unchanged
if (dij > dik + dkj )
D1(ij) = dik+dkj
else D1(ij) = dij
Floyd Warshall Algorithm- programs

14. Shortest Path
A B C D
A - 2 3 6
B 2 - 1 4
C 3 1 - 3
D 6 4 3 -
A B C D
A - 2 2 3
B 1 - 3 3
C 2 2 - 4
D 3 3 3 -
A >> C i=1, j=3
Distance: d13 = 3
Path: S13 = 2 A >> B >> C
S12 = 2 A >> B >> C
2+1 = 3

15. A B C D
A - 2 3 6
B 2 - 1 4
C 3 1 - 3
D 6 4 3 -
A B C D
A - 2 2 3
B 1 - 3 3
C 2 2 - 4
D 3 3 3 -
A >> D i=1, j=4
Distance: d14 = 6
Path: S14 = 3 A >> C >> D
S13 = 2 A >> B >> C >> D
S12 = 2 A >> B >> C >> D
Shortest Path

16.  The running time is O(n3
).
 The space
requirements
are O(n2
)
16
Time and Space Requirements

17. Shortest paths in directed graphs
Transitive closure of directed
graphs.
Inversion of real matrices
Optimal routing.
Maximum bandwidth paths
Computing canonical form of
difference bound matrices
Applications and generalizations

18. My Complete Code
C Programming
http://pastebin.com/s3vBx3KD

19. References
https://en.wikipedia.org/wiki/Floyd
%E2%80%93Warshall_algorithm
https://compprog.wordpress.com/200
7/11/15/all-sources-shortest-path-the-
floyd-warshall-algorithm/

20. Thanks to All