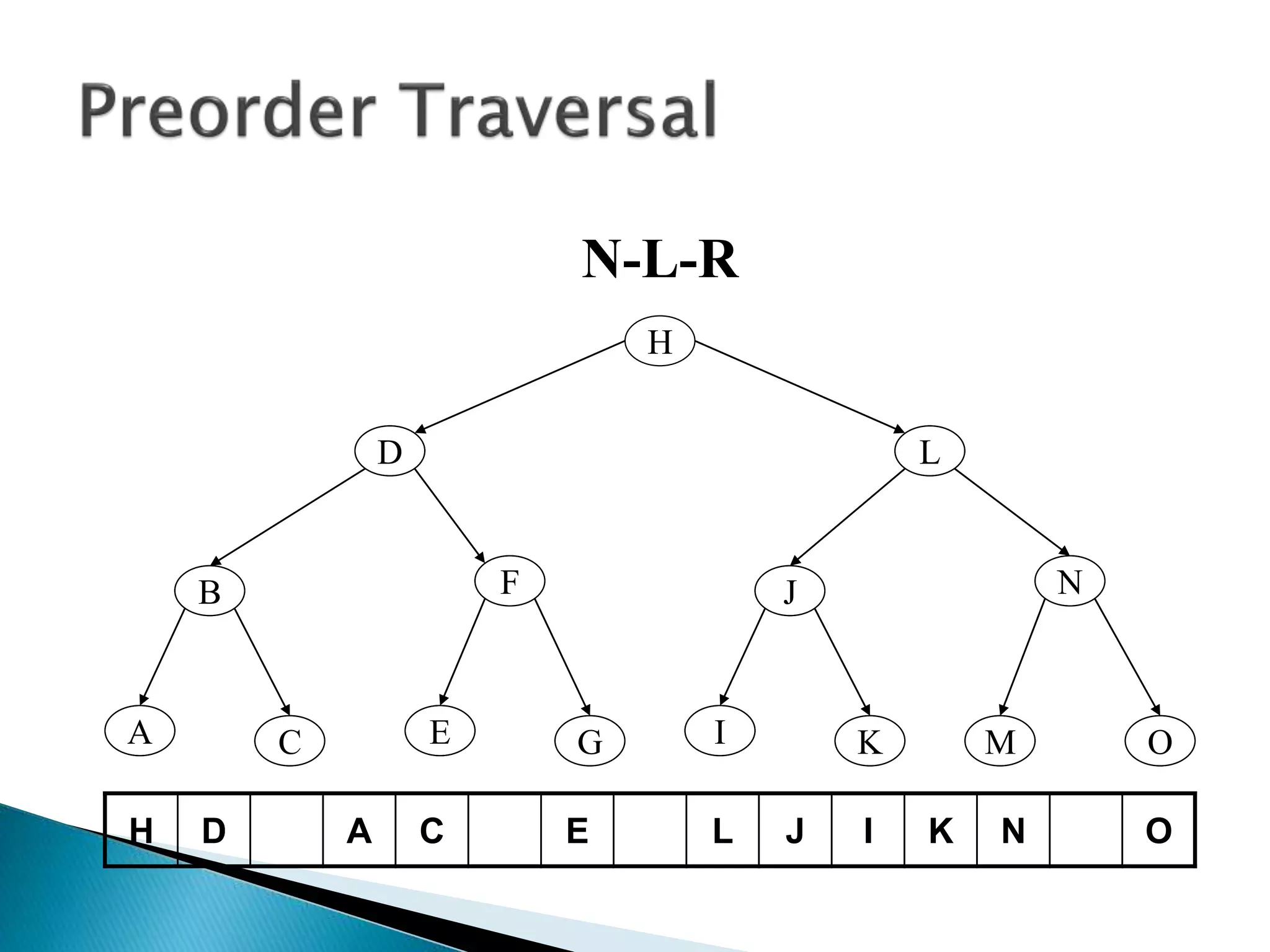
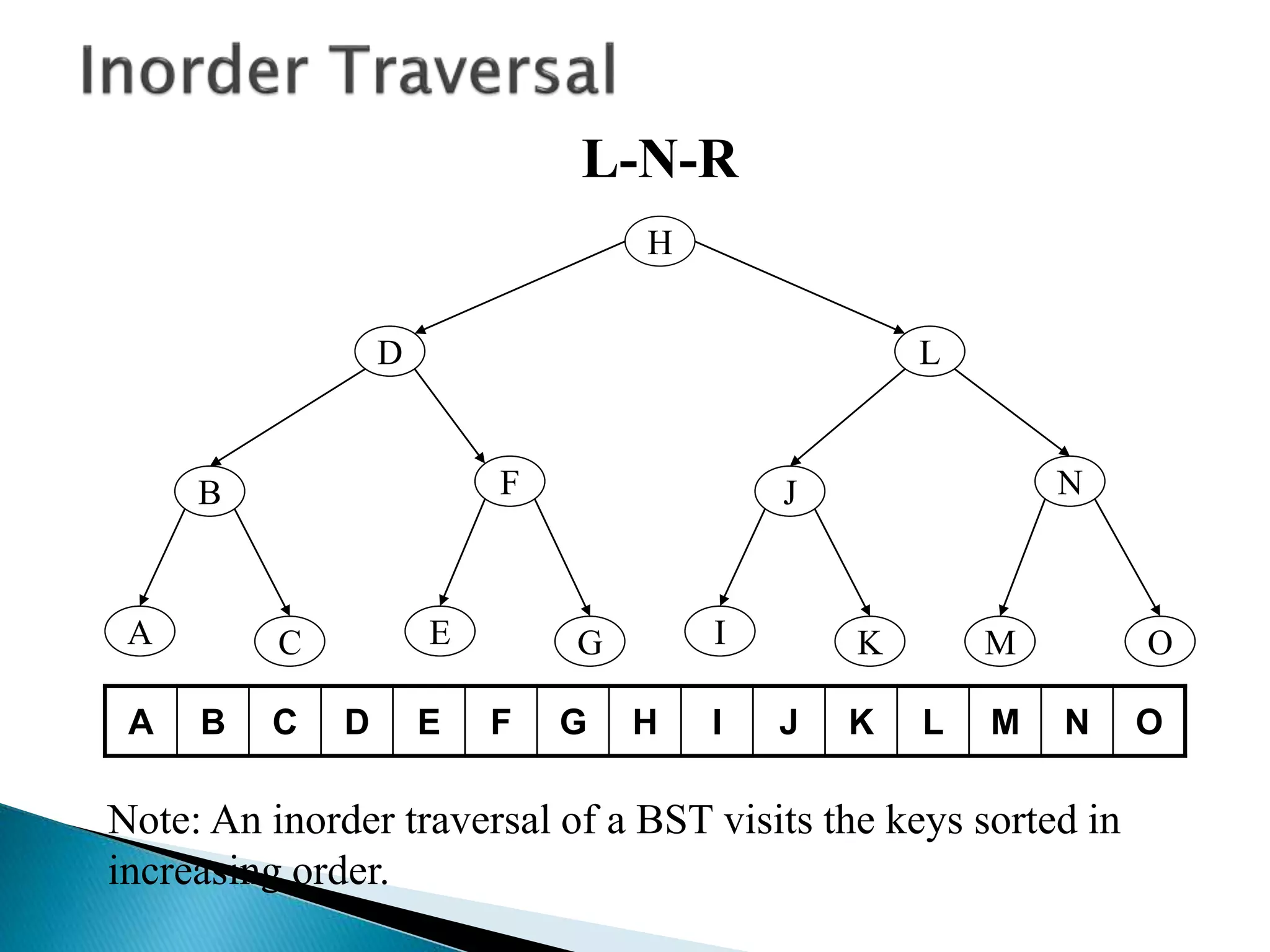
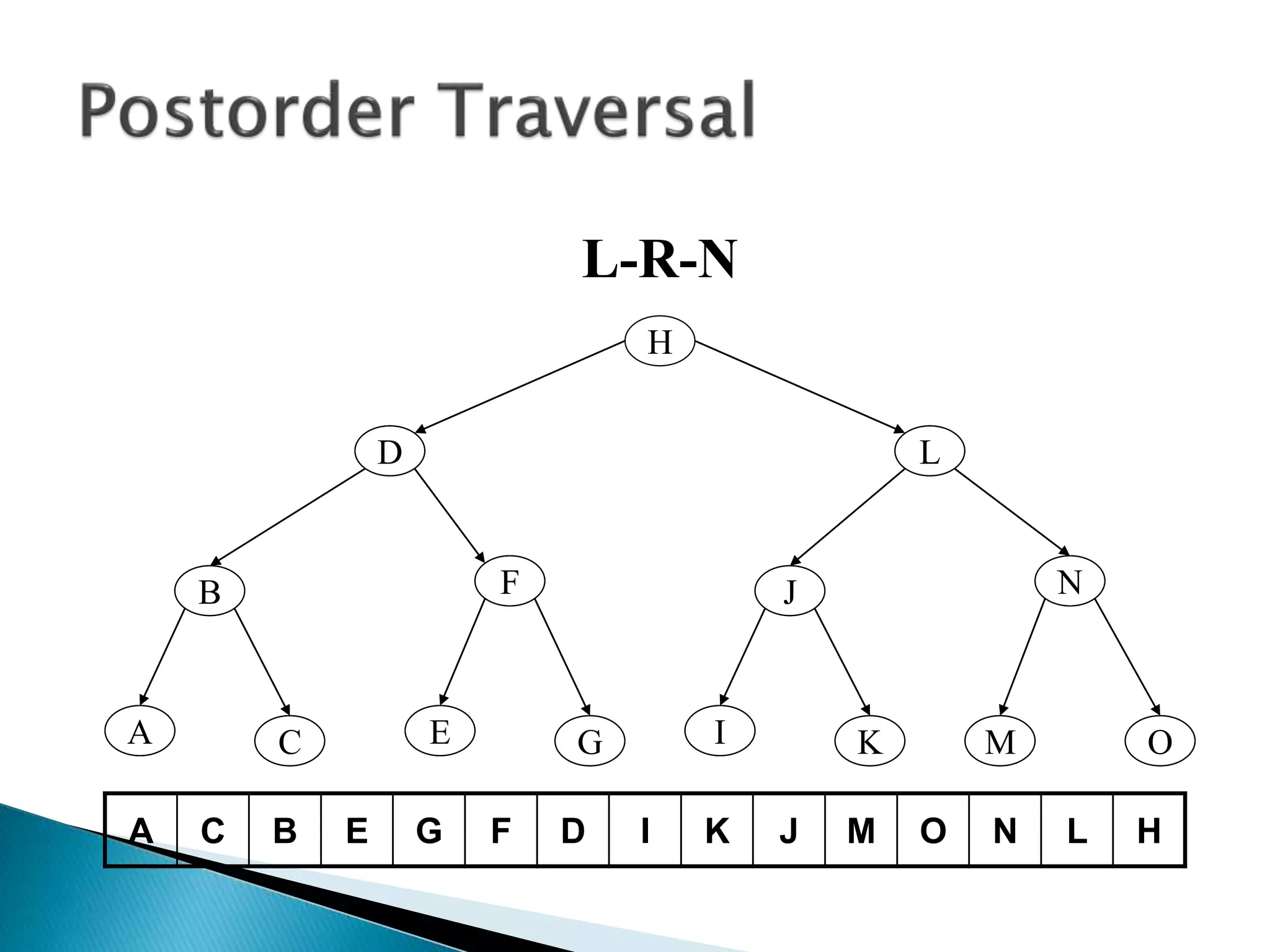
The document discusses tree traversals, which involve systematically visiting each node of a tree. There are three common traversals: preorder, inorder, and postorder. Preorder visits the node, then left subtree, then right subtree. Inorder visits the left subtree, then the node, then the right subtree. Postorder visits the left subtree, then the right subtree, then the node. The document provides examples of these traversals on sample trees.

1.  The process of systematically visiting all
the nodes in a tree and performing some
computation at each node in the tree is
called a tree traversal.

2. H
D
B
N
L
F J
A C E G I K M O
H B F N E G O

3. Name for each Node: CODE
public void displayTree(Node n){
if( n == null ) return;
printf(n.data);
displayTree(n.left);
displayTree(n.right);
}
•Visit the node
•Visit the left subtree, if any.
•Visit the right subtree, if any.
Preorder
(N-L-R)
public void displayTree(Node n){
if( n == null ) return;
displayTree(n.left);
printf(n.data);
displayTree(n.right);
}
•Visit the left subtree, if any.
Visit the node
•Visit the right subtree, if any.
Inorder
(L-N-R)
public void displayTree(Node n){
if( n == null ) return;
displayTree(n.left);
displayTree(n.right);
printf(n.data);
}
•Visit the left subtree, if any.
•Visit the right subtree, if any.
•Visit the node
Postorder
(L-R-N)

4. N-L-R
H
D
B
N
L
F J
A C E G I K M O
H D A C E L J I K N O

5. L-N-R
H
D
B
N
L
F J
A C E G I K M O
A B C D E F G H I J K L M N O
Note: An inorder traversal of a BST visits the keys sorted in
increasing order.

6. L-R-N
H
D
B
N
L
F J
A C E G I K M O
A C B E G F D I K J M O N L H

7.  The children of any node in a binary tree
are ordered into a left child and a right
child
 A node can have a left and
a right child, a left child
only, a right child only,
or no children
 The tree made up of a left
child (of a node x) and all its
descendents is called the left subtree of
x
 Right subtrees are defined similarly
7
8 9
10
1
3
11
5
4 6
7
12

8.  Assume: visiting a node
is printing its label
 Preorder:
1 3 5 4 6 7 8 9 10 11 12
 Inorder:
4 5 6 3 1 8 7 9 11 10 12
 Postorder:
4 6 5 3 8 11 12 10 9 7 1
8
1
3
8 9
11
5
4 6
7
10
12

9.  Assume: visiting a node
is printing its data
 Preorder: 15 8 2 6 3 7
11 10 12 14 20 27 22 30
 Inorder: 2 3 6 7 8 10 11
12 14 15 20 22 27 30
 Postorder: 3 7 6 2 10 14
12 11 8 22 30 27 20 15
9
6
15
8
2
3 7
11
10
14
12
20
27
22 30

10.  Observe the output of the inorder
traversal of the BST example two slides
earlier
 It is sorted
 This is no coincidence
 As a general rule, if you output the keys
(data) of the nodes of a BST using inorder
traversal, the data comes out sorted in
increasing order
10