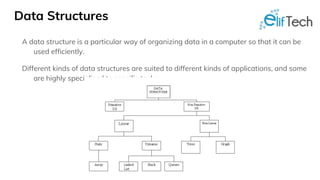
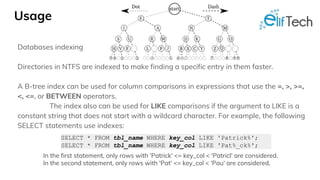
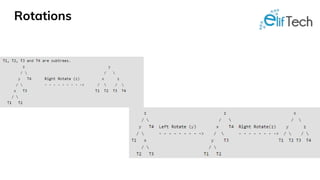
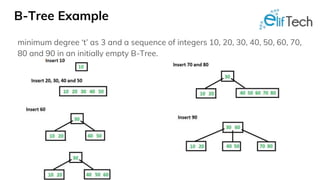
The document discusses various advanced data structures including binary search trees, AVL trees, red-black trees, and B-trees, focusing on their properties, operations, and use cases. It highlights the importance of understanding these structures for optimizing application performance and provides comparisons between different types. Practical applications in databases and the impact of tree balance on efficiency are emphasized.

1. Balance Tree
Volodymyr Synytskyi, software developer at ElifTech

2. Data Structures
A data structure is a particular way of organizing data in a computer so that it can be
used efficiently.
Different kinds of data structures are suited to different kinds of applications, and some
are highly specialized to specific tasks.

3. Advanced data structures
• Binary Indexed Tree or Fenwick Tree
• Segment Tree
• Disjoint sets
• Trie
• K Dimensional Tree
• Sparse Set
• Binary Heap
• Fibonacci heap

5. Binary search tree
Binary search trees keep their keys in sorted order, so that lookup and other operations
can use the principle of binary search:
when looking for a key in a tree (or a place to insert a new key), they traverse the tree
from root to leaf, making comparisons to keys stored in the nodes of the tree and
deciding, based on the comparison, to continue searching in the left or right subtrees.
Algorithm Average Worst Case
Space O(n) O(n)
Search O(log n) O(n)
Insert O(log n) O(n)
Delete O(log n) O(n)
A binary search tree of
size 9 and depth 3, with 8
at the root.

6. Operations
As with all binary trees, a node's in-order successor is its right subtree's left-
most child, and a node's in-order predecessor is the left subtree's right-most
child.
def search_recursively(key, node):
if node is None or node.key == key:
return node
elif key<node.key:
return search_recursively(key, node.left)
else: # key > node.key
return search_recursively(key, node.right)

7. Operations
Deleting a node with two children: call the node to be deleted N. Do not delete N. Instead,
choose either its in-order successor node or its in-order predecessor node, R. Copy the
value of R to N, then recursively call delete on the original R until reaching one of the first
two cases.

8. BST Problem
The problem with BST is that, depending on the
order of inserting elements in the tree, the tree
shape can vary.
In the worst cases (such as inserting elements in
order) the tree will look like a linked list in which
each node has only a right child.

9. Self Balancing BST
AVL Tree
Splay Tree
B Tree
Red-Black Tree
From a practical point of view, B-trees, therefore, guarantee an access time of
less than 10 ms even for extremely large datasets.
—Dr. Rudolf Bayer, inventor of the B-tree

10. Usage
Databases indexing
Directories in NTFS are indexed to make finding a specific entry in them faster.
A B-tree index can be used for column comparisons in expressions that use the =, >, >=,
<, <=, or BETWEEN operators.
The index also can be used for LIKE comparisons if the argument to LIKE is a
constant string that does not start with a wildcard character. For example, the following
SELECT statements use indexes:
SELECT * FROM tbl_name WHERE key_col LIKE 'Patrick%';
SELECT * FROM tbl_name WHERE key_col LIKE 'Pat%_ck%';
In the first statement, only rows with 'Patrick' <= key_col < 'Patricl' are considered.
In the second statement, only rows with 'Pat' <= key_col < 'Pau' are considered.

11. Red Black Trees
Aim to keep the tree balanced without affecting the complexity of the
primitive operations.
This is done by
Coloring each node in the tree with either red or black.
Preserving a set of properties that guarantee that the deepest path in the tree is not longer
than twice the shortest one. Every Red Black Tree with n nodes has height <= 2Log2(n+1)

12. Red Black Trees
A red-black tree is a binary search tree with the following properties:
Every node is colored with either red or black.
All leaf (nil) nodes are colored with black; if a node’s child is missing then we
will assume that it has a nil child in that place and this nil child is always
colored black.
Both children of a red node must be black nodes.
Every path from a node n to a descendent leaf has the same number of black
nodes (not counting node n). We call this number the black height of n,
which is denoted by bh(n).

13. Red Black Trees

14. Red Black Trees
We use two tools to do balancing:
Recoloring
Rotation
Color of a NULL node is considered as BLACK.
Rotation is a binary operation, between a parent node and one of its
children, that swaps nodes and modifys their pointers while preserving the
inorder traversal of the tree (so that elements are still sorted).

15. Red Black Insertion
A BST insertion, which takes O(log n) as shown before.
Fixing any violations to red-black tree properties that may occur after
applying step 1. This step is O(log n) also, as we start by fixing the newly
inserted node, continuing up along the path to the root node and fixing
nodes along that path. Fixing a node is done in constant time and involves
re-coloring some nodes and doing rotations.

16. Red Black Insertion
Perform standard BST insertion and make the color of newly inserted nodes
as RED.
If x is root, change color of x as BLACK (Black height of complete tree
increases by 1).
Do following if color of x’s parent is not BLACK or x is not root.
a) If x’s uncle is RED (Grand parent must have been black)
Change color of parent and uncle as BLACK.
color of grand parent as RED.
Change x = x’s grandparent, repeat steps 2 and 3 for new x.

17. Red Black Insertion
Do following if color of x’s parent is not BLACK or x is not root.
b) If x’s uncle is BLACK, then there can be four configurations for x, x’s parent (p) and x’s
grandparent (g)
Left Left Case (p is left child of g and x is left child of p)
Left Right Case (p is left child of g and x is right child of p)
Right Right Case (Mirror of case a)
Right Left Case (Mirror of case c)

18. Red Black Insertion

20. AVL Tree
AVL tree is a self-balancing Binary Search Tree (BST) where the difference
between heights of left and right subtrees cannot be more than one for all
nodes.
Calculates a balance factor for every node. If balance factor > 1 or < -1 then
node is unbalanced.
The AVL trees are more balanced compared to Red Black Trees, but they
may cause more rotations during insertion and deletion.
So if your application involves many frequent insertions and deletions, then
Red Black trees should be preferred.

21. Rotations

22. Rotations

23. B-Tree
B-tree is a fat tree.
The main idea of using B-Trees is to reduce the
number of disk accesses.
Height of B-Trees is kept low by putting
maximum possible keys in a B-Tree node.
Since h is low for B-Tree, total disk accesses for
most of the operations are reduced
significantly compared to balanced Binary
Search Trees like AVL Tree, Red Black Tree,
..etc.

24. Properties of B-Tree
All leaves are at same level.
A B-Tree is defined by the term minimum degree ‘t’. The value of t depends
upon disk block size.
Every node except root must contain at least t-1 keys. Root may contain
minimum 1 key.
All nodes (including root) may contain at most 2t – 1 keys.
All keys of a node are sorted in increasing order. The child between two keys
k1 and k2 contains all keys in range from k1 and k2.

25. B-Tree
B-Trees grow up unlike BSTs which grow down.

26. B-Tree Example
minimum degree ‘t’ as 3 and a sequence of integers 10, 20, 30, 40, 50, 60, 70,
80 and 90 in an initially empty B-Tree.

27. Links
https://www.topcoder.com/community/data-science/data-science-
tutorials/an-introduction-to-binary-search-and-red-black-trees/
http://www.geeksforgeeks.org/avl-tree-set-1-insertion/
http://www.geeksforgeeks.org/red-black-tree-set-1-introduction-2/
http://www.geeksforgeeks.org/splay-tree-set-1-insert/
http://www.geeksforgeeks.org/b-tree-set-1-introduction-2/

28. TopCoder Practice Problems
• MonomorphicTyper (SRM 286)
• PendingTasks (TCHS SRM 8)
• RedBlack (SRM 155)
• DirectoryTree (SRM 168)
• EncodingTrees (SRM 261)
• AntiChess (SRM 266)
• IncompleteBST (SRM 319)
Quiz
• http://quiz.geeksforgeeks.org/data-structure/balanced-binary-search-trees/

29. Conclusion
Although you may never need to implement your own set or map classes,
thanks to their common built-in support, understanding how these data
structures work should help you better assess the performance of your
applications and give you more insight into what structure is right for a given
task.

30. Thank you for attention!
Find us at eliftech.com
Have a question? Contact us:
info@eliftech.com