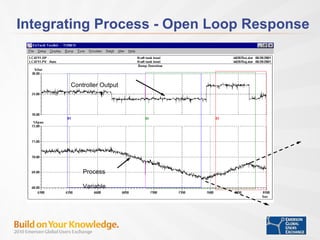
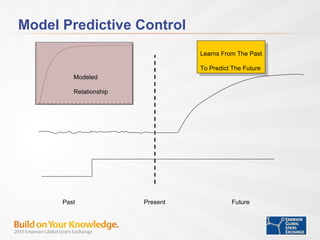
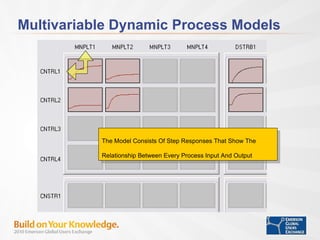
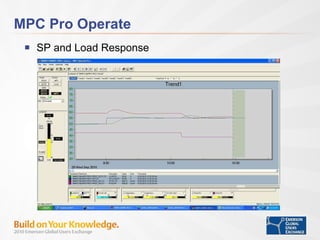
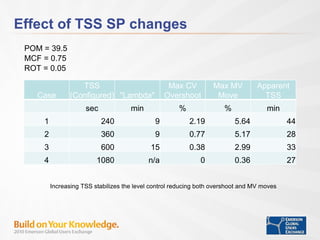
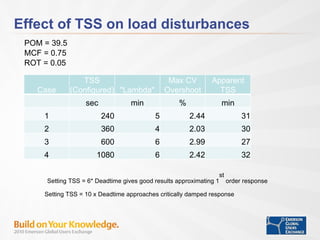
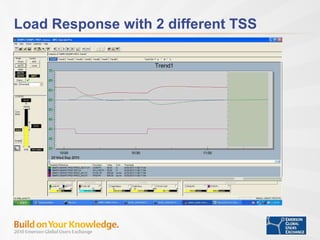
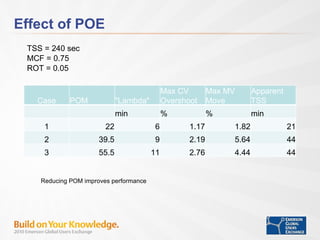
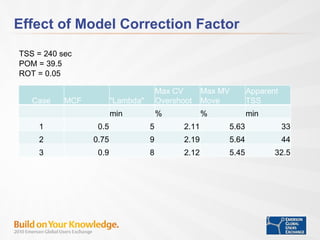
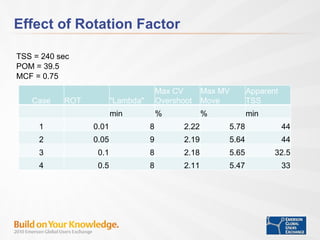
The document discusses controlling integrating processes like liquid levels using model predictive control (MPC). It explains that integrating processes require control since they have no natural equilibrium. The key points covered are: - MPC can effectively control integrating processes by considering feedback, model correction, rotation factors, and tuning parameters. - Tuning time to steady state, penalty on move, and model correction factor impact control performance for setpoint changes and load disturbances. - With proper tuning, MPC provides improved control of integrating processes compared to conventional PI control.

1. Model Predictive Control for Integrating Processes Lou Heavner – Consultant, APC

2. Presenter Lou Heavner

3. Introduction Historically, APC project engineers and consultants have tried to keep level control outside of the MPC solution. Level control and control of other integrating processes are poorly understood by many control engineers. This presentation will attempt to answer the following questions: Can you control level with MPC? How do you control level with MPC? When should you control level with MPC?

4. Integrating Processes Non-Self-Regulating – No natural equilibrium or steady-state Must be controlled Includes most liquid levels, many gas pressure systems, and some other processes Over a short enough time horizon, most processes appear to be integrating Deadtime may be present, but no 1 st order or higher order time constants in open loop response

5. Integrating Process - Open Loop Response Controller Output Process Variable

6. Process Examples Hopper w/ Loss-in-Weight Feeder and Conveyor Large Deadtime Dynamic Distillation Column Bottom Level and Reflux Accumulator Level Multi-variable Interaction Evaporator Level Multi-variable Interaction Large Deadtime Dynamic Oil & Gas Production Separator Level Multi-variable Interaction Slug Control

7. Conventional Control of Integrating Processes PI control is recommended Closed Loop Time Constant (lambda) Lambda - (setpoint change) - time for PV to reach setpoint after a setpoint change Lambda - (load change) - the time required to stop the change in the PV due to a step load change. The level will return to setpoint in about 6 x Lambda. Beall reference describes in great detail

8. Lambda Tuning Rules (Integrating Process) Choose Lambda (λ) Small Lambda reduces process overshoot and shortens process response Small Lambda passes more of the variability “downstream” Rule of thumb: select Lambda as large as possible to attenuate process variability Tr = (2* λ) + Td or if Td<< λ, Tr = 2 *λ Kc = ____ Tr ____ or if Td<< λ, Kc = ___ 2 ____ Kp(λ + Td) 2 Kp* λ

9. Model Predictive Control Handles difficult process dynamics, reduces variability and protects constraints Easy, Fast, Implementation Fully embedded, no integration required Configuration Operator Displays Historian Scaleable, Practical Model Predictive Control PredictPro LP Optimization Large Problems (80x40)

10. Model Predictive Control Learns From The Past To Predict The Future Past Present Future Modeled Relationship

11. Multivariable Dynamic Process Models The Model Consists Of Step Responses That Show The Relationship Between Every Process Input And Output

12. Model Predictive Control of Integrating Processes Factors considered: Feedback mechanism Model Correction Factor Rotation Factor TSS selection MPC Controller “Tuning” POM POE Multivariable Interaction Deadtime

13. Prediction Error Model Correction Factor & Rotation Factor Consider a prediction vector P whose elements are indexed by j. That is j= 0 to 119 since in MPC-PRO the prediction horizon is 120 elements long. The equation for the update of the prediction vector is: P(j) = P(j) + {(1 – R) + j*R}*F Where R is the ROTATION FACTOR and F is the filtered shift measured as the error (i.e. the difference between the first element of the last prediction vector and the feedback measurement) multiplied by the MODEL CORRECTION FACTOR Parameter Names & Default Values Predict Pro: ROTATION_FACTOR[x] = 0.05 Predict: ROT_FACTOR[x] = 0.001 MOD_CORR_FACTOR[x] = 0.75 v10.0+ or 0.4 in earlier versions [x] is the number of the process output Tunable w/o download

14. MPC Tuning Time to Steady-State (TSS) Defines Prediction Horizon Sets Controller execution speed Requires Download Penalty on Move (POM) Slows the control action of MVs (Process Inputs) Makes the controller more robust Powerful, but requires a download to change Penalty on Error (POE) Works on Process Outputs Fine tuning and usually not altered Requires Download

15. MPC Pro Operate SP and Load Response

16. Effect of TSS SP changes Increasing TSS stabilizes the level control reducing both overshoot and MV moves Case TSS (Configured) &quot;Lambda&quot; Max CV Overshoot Max MV Move Apparent TSS sec min % % min 1 240 9 2.19 5.64 44 2 360 9 0.77 5.17 28 3 600 15 0.38 2.99 33 4 1080 n/a 0 0.36 27 POM = 39.5 MCF = 0.75 ROT = 0.05

17. Effect of TSS on load disturbances Setting TSS = 6* Deadtime gives good results approximating 1 st order response Setting TSS = 10 x Deadtime approaches critically damped response Case TSS (Configured) &quot;Lambda&quot; Max CV Overshoot Apparent TSS sec min % min 1 240 5 2.44 31 2 360 4 2.03 30 3 600 6 2.99 27 4 1080 6 2.42 32 POM = 39.5 MCF = 0.75 ROT = 0.05

18. Load Response with 2 different TSS

19. Effect of POE Reducing POM improves performance TSS = 240 sec MCF = 0.75 ROT = 0.05 Case POM &quot;Lambda&quot; Max CV Overshoot Max MV Move Apparent TSS min % % min 1 22 6 1.17 1.82 21 2 39.5 9 2.19 5.64 44 3 55.5 11 2.76 4.44 44

20. Effect of Model Correction Factor TSS = 240 sec POM = 39.5 ROT = 0.05 Case MCF &quot;Lambda&quot; Max CV Overshoot Max MV Move Apparent TSS min % % min 1 0.5 5 2.11 5.63 33 2 0.75 9 2.19 5.64 44 3 0.9 8 2.12 5.45 32.5

21. Effect of Rotation Factor Case ROT &quot;Lambda&quot; Max CV Overshoot Max MV Move Apparent TSS min % % min 1 0.01 8 2.22 5.78 44 2 0.05 9 2.19 5.64 44 3 0.1 8 2.18 5.65 32.5 4 0.5 8 2.11 5.47 33 TSS = 240 sec POM = 39.5 MCF = 0.75

22. Lessons Learned Select TSS Limited by Deadtime Dependant on Self-Regulating responses in multi-variable application Nature of desired “closed-loop” response – Tight Response vs Attenuate Variability Increase TSS to reduce overshoot Start with 6 x deadtime if possible Select Penalty on Move Counter-intuitive for integrating processes Smaller POM reduces overshoot and shortens response Select Model Correction Factor Relatively weak handle Select Rotation Factor Relatively weak handle

23. Where To Get More Information Author: [email_address] (512) 834-7262 References: Beall, James F., Base Process Control Diagnostics and Optimization, Internal Emerson document, 2002. Consulting services Contact your local sales office