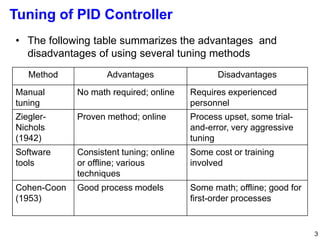
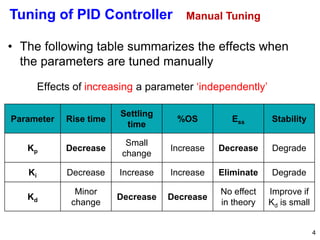
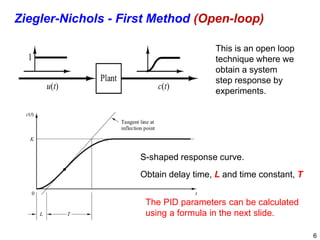
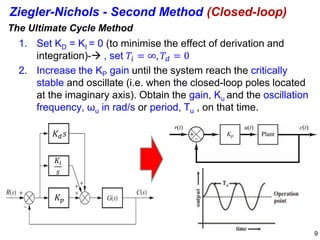
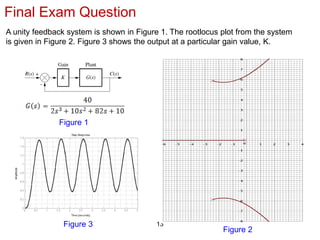
The document discusses PID (Proportional-Integral-Derivative) controller tuning methods, highlighting the use of root locus and various tuning techniques categorized into open-loop and closed-loop approaches. It outlines specific methods like Ziegler-Nichols and Cohen-Coon, detailing their advantages and disadvantages, as well as the effects on system parameters during manual tuning. Additionally, it emphasizes the necessity of fine-tuning following initial setups to achieve acceptable performance in control systems.

1. Dr. Mohamed Sultan bin Mohamed Ali
Department of Electrical Engineering
College of Engineering
Qatar University
Control Systems
MECE 352
Lecture 13
PID Tuning Method

2. 2
Tuning of PID Controller
 The PID controller is widely used in the industries in which the
Kp, Ki and Kd parameters can often be easily adjusted.
 The root locus is one of the techniques to obtain the PID
gains.
 There are several other methods for tuning a PID controller.
 The tuning generally involve the choosing of parameters Kp, Ki
and Kd
 The methods can be divided into open-loop and closed-loop
approaches.
 Closed loop:
• Ziegler-Nichols, Tyreus-Luyben, Damped oscillation
methods
 Open-loop:
• Ziegler-Nichols, Cohen Coon, Fertik, Minimum error
criteria

3. • The following table summarizes the advantages and
disadvantages of using several tuning methods
3
Method Advantages Disadvantages
Manual
tuning
No math required; online Requires experienced
personnel
Ziegler-
Nichols
(1942)
Proven method; online Process upset, some trial-
and-error, very aggressive
tuning
Software
tools
Consistent tuning; online
or offline; various
techniques
Some cost or training
involved
Cohen-Coon
(1953)
Good process models Some math; offline; good for
first-order processes
Tuning of PID Controller

4. • The following table summarizes the effects when
the parameters are tuned manually
Effects of increasing a parameter ‘independently’
4
Manual Tuning
Parameter Rise time
Settling
time
%OS Ess Stability
Kp Decrease
Small
change
Increase Decrease Degrade
Ki Decrease Increase Increase Eliminate Degrade
Kd
Minor
change
Decrease Decrease
No effect
in theory
Improve if
Kd is small
Tuning of PID Controller

5. 5
• This method is useful when mathematical model of a plant
cannot be easily obtained or not known.
• The method uses experimental approaches to tune the
PID controllers.
• However, the resulting system may exhibit a large
maximum overshoot in the step response, which is
unacceptable. Then a series of fine tuning to obtain
acceptable results is needed.
• The Z-N tuning rules gives an educated guess for the
parameter values, and provide a starting point for fine
tuning, not a final parameter values.
• There are two methods called Z-N tuning rules: Open-loop
and closed-loop.
Ziegler-Nichols Method
Tuning of PID Controller

6. 6
S-shaped response curve.
Obtain delay time, L and time constant, T
This is an open loop
technique where we
obtain a system
step response by
experiments.
The PID parameters can be calculated
using a formula in the next slide.
Ziegler-Nichols - First Method (Open-loop)

7. 7
Ziegler-Nichols - First Method (Open-loop)

8. 8
Function C(s)/R(s) may then be
approximated by a first-order system
with a transport lag as follows:
The PID controller tuned by the
first method of Ziegler–Nichols
rules gives ;
PID controller has a pole at the origin and double zeros at s=–1/L
𝐶𝐶(𝑠𝑠)
𝑅𝑅(𝑠𝑠)
=
𝐾𝐾𝑒𝑒−𝐿𝐿𝐿𝐿
𝑇𝑇𝑇𝑇 + 1
Ziegler-Nichols - First Method (Open-loop)

9. 1. Set KD = KI = 0 (to minimise the effect of derivation and
integration)- , set 𝑇𝑇𝑖𝑖 = ∞, 𝑇𝑇𝑑𝑑 = 0
2. Increase the KP gain until the system reach the critically
stable and oscillate (i.e. when the closed-loop poles located
at the imaginary axis). Obtain the gain, Ku and the oscillation
frequency, ωu in rad/s or period, Tu , on that time.
9
Ziegler-Nichols - Second Method (Closed-loop)
The Ultimate Cycle Method
𝐾𝐾𝑑𝑑𝑠𝑠
𝐾𝐾𝑖𝑖(𝑠𝑠)
𝐾𝐾𝑖𝑖
𝑠𝑠
𝐾𝐾𝑝𝑝

10. 10
3. Calculate the KP gain that is supposedly needed using
formula in the table.
4. Based on the required type of controller, calculate the
necessary gain using formulas in the table.
Ziegler-Nichols - Second Method (Closed-loop)
𝐺𝐺𝑃𝑃𝑃𝑃𝑃𝑃 𝑠𝑠 = 𝐾𝐾𝑝𝑝 1 +
1
𝑇𝑇𝑖𝑖𝑠𝑠
+ 𝑇𝑇𝐷𝐷𝑠𝑠

11. Example 1
• Design a PID controller using Ziegler-Nichols tuning method
for unity feedback system with the open loop system which
is given as:
11

12. Final Exam Question
13
A unity feedback system is shown in Figure 1. The rootlocus plot from the system
is given in Figure 2. Figure 3 shows the output at a particular gain value, K.
Figure 1
Figure 2
Figure 3