This document provides a marking scheme for an Additional Mathematics paper 2 trial examination from 2010. It consists of 7 questions, each with multiple parts. For each question, it lists the number of marks awarded for various steps in the solutions, such as setting up the correct formula, performing calculations accurately, obtaining the right solution, plotting points correctly, and using appropriate mathematical reasoning. The highest number of marks for a single question is 8 marks. The marking scheme evaluates multiple aspects of students' work and reasoning for 7 multi-step mathematics problems.

1. MARKING SCHEME
ADDITIONAL MATHEMATICS PAPER 2
SPM TRIAL EXAMINATION 2010
N0. SOLUTION MARKS
1 x = 10 − 2 y P1
K1 Eliminate x
y 2 + (10 − 2 y ) y = 24
y 2 − 10 y + 24 = 0 K1 Solve quadratic
( y − 4) ( y − 6) = 0 equation
y=4 or y=6
N1
x=2 or x = −2
N1
5
2
(a) k=6 P1
(b) Mid point 23 , 28 , 33 , 38 , 43 P1
(i) Mean
=
∑ fx =
1 × 23 + 4 × 28 + 7 × 33 + 5 × 38 + 3 × 43
K1 Use formula and
calculate
∑f 1+ 4 + 7 + 5 + 3
685
= = 34.25 N1
20
(ii) Varian
=
∑ fx2 − x 2
∑f K1 Use formula and
1 × 232 + 4 × 282 + 7 × 332 + 5 × 382 + 3 × 432 calculate
= − 34.252
20
24055
= − 34.252
20 N1
= 29.69
(iii) Median , m
1  1  K1 Use formula and
 2N −F   2 (20) − 5  calculate
= L+  C = 30.5 +  5
 fm   7 
    N1
= 34.07
8
2

2. N0. SOLUTION MARKS
3 1
y = x3 − x 2 + 2
3
(a) dy
= x2 − 2 x = 3 K1 Equate and solve
dx
x2 − 2 x − 3 = 0 quadratic
equation
( x + 1) ( x − 3) = 0
x = −1 , 3
2
x = −1 y=
3
x=3 y=2
 2
 −1,  and ( 3, 2 ) N1 N1
 3
(b) Equation of normals :
1
mnormal = −
3 K1 Use mnormal to form
2 1 1 equations
y− = − ( x + 1) y−2=− ( x − 3)
3 3 3
1 1 1 N1 N1
y=− x+ or equivalent y = − x+3 or equivalent
3 3 3
6
4
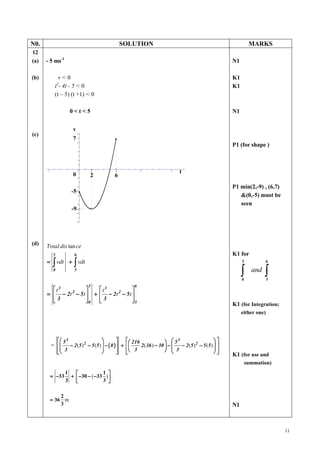
y
(a)
P1 Modulus sine
shape correct.
2 y = 3sin 2 x − 1
P1 Amplitude = 3
[ Maximum = 2
1
and Minimum =
-1]
O π π 3π 2π x P1 Two full cycle in
-1 2 2 0 ≤ x ≤ 2π π
3x
y = 1−
-2
2π P1 Shift down the
graph
3

3. N0. SOLUTION MARKS
4
3x
(b) 3sin 2 x − 1 = 1 −
2π
or N1 For equation
3x
y = 1−
2π
3x
Draw the straight line y = 1− K1 Sketch the
2π straight line
Number of solutions = 5. N1
7
5
(a) Common ratio, r=4 N1
(b) 1 K1
A6 = π ( 32 ) 1
T6 = ar = π ( 4 )
2 5 5
4 OR 4
N1
= 256π = 256π
(c)
S6 − S 2 K1 Use S6 or S2
1
(
π 46 − 1
1
) (
π 42 − 1 ) K1 Use S6 - S2
= 4 −4
4 −1 4 −1
N1
= 341.25π −1.25π
= 340π
6
4

4. N0. SOLUTION MARKS
6
(a) K1 for using vector
(i) uuu uuu uuu
r r r triangle for a(i) or
OD = OC + CD
a(ii)
= 6a + 12b
% % N1
(ii) uuu uuu uuu
r r r
AB = OB − OA
1 uuu uuu
r r
= OD − OA
2
= 3a + 6b − 3a
% % % N1
= 6b
%
OR
uuu 1 uuu
r r
AB = CD = 6b [ K1 N1 ]
2 %
(b)
uuur
AE
uuu uuu
r r
= AB + BE K1 for using vector
uuu
r
 1 uuu 
r triangle and BE
= 6b + h  OD 
% 2 
= 6b + h ( 3a + 6b )
% % %
a + kb = 3ha + ( 6 + 6h ) b
K1
% % % %
k = 6 + 6h K1 for equating
3h = 1 coefficients
1
1 = 6 + 6  correctly
h=  3
3
=8 N1 N1
8
5

5. N0. SOLUTION MARKS
7
(a)
x 1 2 3 4 5 6
N1 6 correct
log10 y 0.65 0.87 1.08 1.30 1.52 1.74
values of log y
log10 y
(b) K1 Plot log10 y vs x
Correct axes &
uniform scale
N1 6 points plotted
correctly
N1 Line of best-fit
0.43
0 x
(c) log10 y = ( k log10 A ) x + log10 A P1
(i) x = 2.6 N1
(ii) y-intercept = log10 y K1
A = 2.69 N1
gradient = k log10 A K1
gradient
k=
log10 A *
= 0.51 N1
10
6

6. N0. SOLUTION MARKS
8
(a) P(5, 1 ) P1
Q(1, 0 ) P1
(b) 1
∫ (4y + 1) dy ∫ x dy
2
A= K1 use
0
K1 correct limit
 4y3  1
=  + y
 3  0
K1 integrate
correctly
7
= OR equivalent
3 N1
5
x −1
(c) V= π∫ dx K1 integrate
4
1
π ∫ y 2 dx
K1 correct limit
π  x2 5
=  − x
4 2  1
K1 integrate
correctly
= 2π N1
10
7

7. N0. SOLUTION MARKS
9
(a) 4 K1 Use ratio of
cos ∠ POQ =
10 trigonometry or
equivalent
∠ POQ = 1.16 rad.
N1
(b)
( 2π – 1.16 ) rad P1
PQ = 10 ( 2π – 1.16 ) K1 Use s = rθ
= 51.24 cm N1
(c)
P1
10 2 − 4 2
= 9.17 cm
1 K1
Area of trapezium POQR = ( 6 + 10 ) × 9.17 *
2
= 73.36 cm2
1 K1 Use formula
Area of sector POQ = (10) 2 (1.16)
2 1
A = r 2θ
= 58 cm2 2
Area of shaded region
= 73.36 – 58 K1
= 15.36 cm2 N1
10
8

8. N0. SOLUTION MARKS
10.
(a) Equation of str. line PQR :
1 K1
m= −
2
1 N1
y= − x+1
2
(b) 1 K1 solving
2x + 6 = − x+1
2 simultaneous
equation
P( –2, 2) N1
(c) 1( x) + 2(−2) 1( y ) + 2(2) K1 Use the ratio
=0 or =1
1+ 2 1+ 2 rule
R( 4, –1) N1
(d)
(i) 1 K1 Use distance
( x − 4) 2 + ( y + 1) 2 = ( x + 2) 2 + ( y − 2) 2
2 formula
4 [ x2 – 8x + 16 + y2 + 2y +1 ] = x2 + 4x + 4 + y2 – 4y +4
x2 + y2 – 12x + 4y + 15 = 0 N1
(ii) Substitute x = 0, y2 + 4y + 15 = 0 K1 Substitute x = 0
b2 – 4ac = (4)2 – 4(1)(15) 2
and use b – 4ac
= – 44 < 0 to make a
conclusion
⇒ No real root for y,
⇒ The locus does not intercept the y-axis. N1 if b2 – 4ac = -44
9

9. 10
N0. SOLUTION MARKS
11
(a)
µ = 80, σ = 12
65 − 80 X −µ
P ( X ≥ 65 ) = P ( Z ≥ ) K1 Use Z =
12 σ
= P ( Z ≥ − 1.25 )
= 1 – 0.1056 K1 Use 1 – Q(Z)
= 0.8944 N1
(b) 0.1056 × 4000 K1
= 422 or 423 N1
(c) 200 P1
= 0.05
4000
Q( Z ) = 0.05
Z = 1.645 K1 Find value of Z
m − 80 m−µ
= − 1.645 K1 Use
12 σ
K1 Use negative
value
m = 60.26 g N1
10
10

10. N0. SOLUTION MARKS
12
(a) - 5 ms-1 N1
(b) v<0 K1
2
t - 4t - 5 < 0 K1
(t – 5) (t +1) < 0
0<t<5 N1
v
(c) 8
7 7
6
P1 (for shape )
4
2
-5
0
0 2 5 6 10 15
t
-2
2 6
-4
P1 min(2,-9) , (6,7)
-5 -5
-6 &(0,-5) must be
-8 seen
-9 -9
-10
-12
(d) Total dis tan ce
5 6 K1 for
= ∫ vdt ∫
+ vdt 5 6
0 5
∫
0
and ∫ 5
5 6
t3  t3 
=  − 2t 2 − 5 t  +  − 2 t 2 − 5 t 
3
 0
 3
 5

K1 (for Integration;
either one)
 5 3    216  5
3 
=  − 2 (5 ) 2 − 5 (5 )  − ( 0 )  +   2( 36 ) − 30  −  − 2 (5 ) 2 − 5 (5 )  
 3


   3
    3


 K1 (for use and
summation)
1  1 
= −33 +  −30 − (−33 ) 
3  3 
2
= 36 m
3 N1
11

11. 10
N0. SOLUTION MARKS
13
P09
(a) × 100 = 125 K1
60
N1
P09 = RM 75
(b) (125 × 4 ) + (120 m) + (80 × 5 ) + 150 m + 450 K1
(i) 120 =
12 + 2 m
K1 (use formula)
1440 + 240 m = 1350 + 270 m
N1
m = 3
(ii)
100
P07 = RM 30 × K1
120
N1
= RM 25
(c)
120 + (120 × 0.15) = 138 K1
K1
(125 × 4 ) + (138 × 3) + (80 × 5 ) + (150 × 6 )
I 10 / 07 =
18
N1
= 123
12

12. 10
N0. SOLUTION MARKS
14
(a) y ≥ 200 N1
x+y ≤ 800 N1
4x + y ≤ 1400 N1
(b) y
1000
4x + y = 1400
900
800
700
600 (200,600)
500
400
R
300
y = 200
200
100
x + y = 800
x
100 200 300 400 500 600 700 800 900
• At least one straight line is drawn correctly from inequalities K1
involving x and y.
N1
• All the three straight lines are drawn correctly
• Region is correctly shaded N1
(c)
(i)
650 N1
(ii)
Maximum point (200, 600) N1
Maximum profit = 20(200) + 6(600) K1
= RM 7600 N1
13

13. 10
N0. SOLUTION MARKS
15
(a) TQ2 = 92 + 62 – 2(9)(6)cos56o K1
TQ = 7.524 cm N1
(b) sin ∠QTR sin 56 0 K1
=
6 7.524
∠QTR = 41o 23’ N1
(c) 1 K1
42.28 = ( RS )(6 )sin 56 o
2
RS = 17
ST = 17 − 9 (or ST + 9 in formula of area) K1
= 8 cm N1
(d) 1
Area ∆ QTR = (9)(6) sin 56 0
2 K1
2
= 22.38 cm
Area of quadrilateral PQTS = 2(42.28) – 22.38 K1
= 62.18 cm2 N1
10
END OF MARKING SCHEME
14