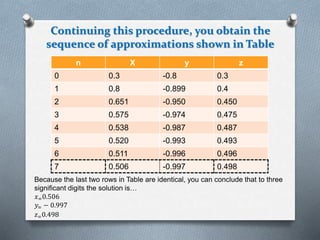
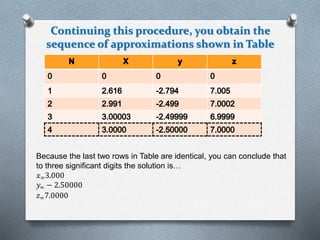
The document discusses iterative methods for solving systems of linear equations, specifically Jacobi's method and Gauss-Seidel method. It provides examples of using these methods to solve several systems of 3 equations with 3 unknowns. For each system, it shows rewriting the equations in a form suitable for the methods, choosing initial approximations, iterating to obtain better approximations, and concluding when subsequent iterations yield identical results to 3 significant digits.

1. Name: (1) Kamal Akhtar F.(120450119156)
Branch: Mechanical-4C(1)
Collage: S.V.M.I.T.

2. Introduction…
O Iteration method:-
O Why iteration method is need?
O When the system of algebraic equation consist of large
number of equation then the direct method becomes
cumbersome and time consuming.
O In this case Iteration method provide easy to
solve the system.
O In Iteration method we start from initial approximation to the
actual solution and obtain better and better approximation
after repeating iteration.
O Iteration method gives the value to the desired accuracy.

3. Iteration method:-
O(1) Jacobi's method
O(2) Gauss-Seidel method

4. Jacobi's method
O A set of n equations and n unknowns:
11 1 12 2 13 3 1 1 a x a x a x ... a x b n n     
21 1 22 2 23 3 2n n 2 a x  a x  a x ... a x  b
. .
. .
. .
n n n nn n n a x  a x  a x ...  a x  b 1 1 2 2 3 3
O note: assume all the diagonal elements
are not zero.

5. Jacobi's method
O If diagonal elements are zero then we
Rewrite the question as…
O 푥1 =
[푏1− 푎11푥2+푎13푥3+⋯+푎1푛푥푛 ]
푎11
O 푥2 =
[푏2− 푎21푥2+푎23푥3+⋯+푎2푛푥푛 ]
푎22
O 푥푛 =
[푏푛− 푎푛1푥2+푎푛2푥2+⋯+푎푛(푛−1)푥푛−1 ]
푎푛푛

6. Jacobi's method
O Suppose that the initial solution is…
O 푥(1
0), 푥(2
0), … , 푥푛
(0) put this all value in the
above equation then we obtain the 1푠푡
approximation to solution as 푥(1
1), 푥2
(1), … ,
푥푛
(1).
O Against the put this value in above equation
then we obtain the 2푛푑 approximation to
solution as 푥(((1
2), 푥2
2), … , 푥푛
2).
O Continues the process of finding the
approximation till get the solution is the
desired level of accuracy.

7. Use the Jacobi method to approximate the solution of
the following system of linear equations.
ퟓ풙ퟏ − ퟐ풙ퟐ+ퟑ풙ퟑ = −ퟏ
−ퟑ풙ퟏ + ퟗ풙ퟐ+풙ퟑ = ퟐ
ퟐ풙ퟏ − 풙ퟐ − ퟕ풙ퟑ = ퟑ
Continue the iterations until two successive approximations are
identical when rounded to three significant digits.
O Solution:--
O 풙ퟏ = −
ퟏ
ퟓ
+
ퟐ
ퟓ
풙ퟐ −
ퟑ
ퟓ
풙ퟑ
O 풙ퟐ =
ퟐ
ퟗ
+
ퟑ
ퟗ
풙ퟏ −
ퟏ
ퟗ
풙ퟑ
O 풙ퟑ = −
ퟑ
ퟕ
+
ퟐ
ퟕ
풙ퟏ −
ퟏ
ퟕ
풙ퟐ
O Because we do not know the actual solution, choose
O 풙ퟏ = ퟎ, 풙ퟐ = ퟎ, 풙ퟑ = ퟎ …Initial approximation
O as a convenient initial approximation. So, the first approximation is
O 풙ퟏ = −
ퟏ
ퟓ
+
ퟐ
ퟓ
ퟎ −
ퟑ
ퟓ
ퟎ ≈ −0.200
O 풙ퟐ =
ퟐ
ퟗ
+
ퟑ
ퟗ
(ퟎ) −
ퟏ
ퟗ
(ퟎ) ≈ ퟎ. ퟐퟐퟐ
O 풙ퟑ = −
ퟑ
ퟕ
+
ퟐ
ퟕ
ퟎ −
ퟏ
ퟕ
ퟎ ≈ −ퟎ. ퟒퟐퟗ

8. Continuing this procedure, you obtain the
sequence of approximations shown in Table
푛 푥1 푥2 푥3
0 0.000 0.000 0.000
1 -0.200 0.200 -0.429
2 0.146 0.203 -0.517
3 0.192 0.328 -0.416
4 0.181 0.332 -0.421
5 0.185 0.329 -0.424
6 0.186 0.331 -0.423
7 0.186 0.331 -0.423
Because the last two rows in Table are identical, you can conclude that
to three significant digits the solution is…
푥1=0.186
푥2=0.331
푥3= − 0.423

9. The Gauss-Seidel Method
O A modification of the Jacobi method called the Gauss-Seidel method.
O This modification is no more difficult to use than the Jacobi method,
and it often requires fewer iterations to produce the same degree of
accuracy.
O With the Jacobi method, the values of 풙풊 obtained in the nth
approximation remain unchanged until the entire(풏 + ퟏ)th
approximation has been calculated.
OWith the Gauss- Seidel method…
O On the other hand, you use the new values of each 풙풊 as soon as they
are known. That is, once you have determined 풙ퟏ from the first
equation, its value is then used in the second equation to obtain the
new 풙ퟐ Similarly, the new 풙ퟏ& 풙ퟐare used in the third equation to
obtain the new풙ퟑ and so on. This procedure is demonstrated in 풙풏.

10. (1)Using the gauss-seidel method to solve the system…
ퟖퟑ풙 + ퟏퟏ풚 − ퟒ풛 = ퟗퟓ,
ퟕ풙 + ퟓퟐ풚 + ퟏퟑ풛 = ퟏퟎퟒ,
ퟑ풙 + ퟖ풚 − ퟐퟗ풛 = ퟕퟏ,
O Solution…- rewriting the equation as...
95−11푦+4푧
O 푥 =
83
= 1.145 − 0.133푦 + 0.048푧
O y=
104−7푥−13푧
52
= 2 − 0.135 − 0.25푧
O z=
71−3푥+8푦
29
= 2.448 − 0.103푥 + 0.276푦
O Assume the initial solution:…
O 푥 = 푦 = 푧 = 0

11. Continuing this procedure, you obtain the
sequence of approximations shown in Table
n X Y Z
0 0 0 0
1 1.145 1.845 1.821
2 0.987 1.412 1.957
3 1.051 1.369 1.962
4 1.057 1.367 1.962
5 1.057 1.367 1.962
Because the last two rows in Table are identical, you can
conclude that to three significant digits the solution is…
푥=1.057
푦=1.367
푧=1.962

12. (2)Using the gauss-seidel method to solve the system…
6풙 + 풚 + 풛 = ퟏퟎퟓ,
4풙 + ퟖ풚 + ퟑ풛 = ퟏퟓퟓ,
5풙 + ퟒ풚 − ퟏퟎ풛 = ퟔퟓ,
O Solution…- rewriting the equation as...
105−푦−푧
O 푥 =
6
= 17.5 − 0.167푦 − 0.167푧
O y=
155−4푥−3푧
8
= 19.375 − 0.5푥 − 0.375푧
O z=
−65+5푥+4푦
10
= −6.5 − 0.5푥 + 0.4푦
O Assume the initial solution:…
O 푥 = 푦 = 푧 = 0

13. Continuing this procedure, you obtain the
sequence of approximations shown in Table
n X y z
0 0 0 0
1 17.5 10.625 6.5
2 14.64 9.618 4.667
3 15.114 10.068 5.084
4 14.970 9.984 4.979
5 15.001 10.007 5.003
Because the last two rows in Table are identical, you can
conclude that to three significant digits the solution is…
푥=15.001
푦=10.007
푧=5.003

14. (3)Using the Gauss-Seidel method to solve the system…
2풙 − 풚 + ퟐ풛 = ퟑ,
풙 + ퟑ풚 + ퟑ풛 = −ퟏ,
풙 + ퟐ풚 + ퟓ풛 = ퟏ,
start with the initial approximations 풙 = ퟎ. ퟑ, 풚 = −ퟎ. ퟖ, 풛 = ퟎ. ퟑ
O Solution…- rewriting the equation as...
3+푦−2푧
O 푥 =
2
= 1.5 + 0.5푦 − 푧
O y=
−1−푥−3푧
3
= −0.333 − 0.333푥 − 푧
O z=
1−푥−2푦
5
= 0.2 − 0.2푥 − 0.4푦
O Assume the initial solution:…
O 푥 = 푦 = 푧 = 0

15. Continuing this procedure, you obtain the
sequence of approximations shown in Table
n X y z
0 0.3 -0.8 0.3
1 0.8 -0.899 0.4
2 0.651 -0.950 0.450
3 0.575 -0.974 0.475
4 0.538 -0.987 0.487
5 0.520 -0.993 0.493
6 0.511 -0.996 0.496
7 0.506 -0.997 0.498
Because the last two rows in Table are identical, you can conclude that to three
significant digits the solution is…
푥=0.506
푦= − 0.997
푧=0.498

16. (4)Using the Gauss-Seidel method to solve the system…
3풙 − ퟎ. ퟏ풚 − ퟎ. ퟐ풛 = ퟕ. ퟖퟓ,
0.1풙 + ퟕ풚 − ퟎ. ퟑ풛 = −ퟏퟗ. ퟑ,
0.1풙 − ퟎ. ퟐ풚 + ퟏퟎ풛 = ퟕퟏ. ퟒ,
start with the initial approximations 풙 = ퟎ. ퟑ, 풚 = −ퟎ. ퟖ, 풛 = ퟎ. ퟑ
O Solution…- rewriting the equation as...
7.85+0.1푦+0.2푧
O 푥 =
3
= 2.616 + 0.033푦 + 0.66z
O 푦 =
1−19.3−0.1푥+0.3푧
7
= −2.757 − 0.014푥 + 0.042푧
O 푧 =
71.4−0.3푥+0.2푦
10
= 7.14 − 0.3푥 − 0.02푦
O Assume the initial solution:…
O 푥 = 푦 = 푧 = 0

17. Continuing this procedure, you obtain the
sequence of approximations shown in Table
Because the last two rows in Table are identical, you can conclude that
to three significant digits the solution is…
푥=3.000
푦= − 2.50000
푧=7.0000